Треугольник Паскаля

Однажды я медленно шёл по Парижу, разглядывал витрины магазинов и читал вывески. Цветастая надпись над входом грязновато‑серого здания настойчиво приглашала зайти и попытать счастья. Я удивился, что игорный дом работает среди бела дня, – это не соответствовало сведениям, почерпнутым мною из классической литературы – и… я зашел. Взору представилась поразительная картина: десятки людей стояли лицом к стене, и перед каждым находился цветной ящик. Подойдя ближе, я увидел, что они либо нажимали кнопку, либо дергали за ручку, будто заводя заглохший лодочный мотор.

Через несколько минут я понял, в чем дело: люди играли с автоматами. Зрелище это неприятное, но великолепное поле для наблюдений психолога. Человек играет с судьбой. Один на один. Все побочные обстоятельства отсеяны. Нет ни соперничеств, ни личной неприязни, ни необходимости скрывать свои чувства.

Есть автоматы, у которых вы можете выиграть только конфетку или сигареты, есть такие, которые играют на деньги, и, наконец, существует возможность наслаждаться игрой безгранично, вступив в единоборство с автоматом, выигрыш у которого дает лишь право дальнейшей игры. Бессмысленно, не правда ли? Но вот так оно есть. Эти автоматы вы можете найти в любом баре, в любом кафе любого города Америки и Западной Европы.

В чем же состоит игра? В принципе она сводится к следующему. Выпускается на волю шарик, который под действием силы тяжести или щелчка пружины движется по доске, на которой установлены препятствия. От каждой преграды шарик может отскочить куда попало. Получив несколько десятков таких случайных щелчков, шарик добирается до дна ящика и успокаивается в каком‑то положении.

В зависимости от формы преград и от того, как они установлены, разные места дна ящика будут достижимы в различной степени. Определив из многочисленных опытов значения вероятностей окончания путешествия шарика в том или ином конечном пункте, нетрудно построить правила игры, которые позволят автомату уверенно обыгрывать своего живого партнера.

В самой простой своей форме игровой автомат похож на так называемую доску Гальтона, которую используют в лекционных демонстрациях.

Прошу взглянуть на рисунок. В воронку насыпаются шарики. По очереди они мчатся вниз, отскакивают то вправо то влево от препятствий и наконец достигают какой‑то ячейки. В качестве препятствий можно брать шестиугольные бляшки или вбить в доску гвоздики. Для доски Гальтона разработана детальная теория. Мы попытаемся обойтись без нее и предположить, что от каждого гвоздика шарик с равной вероятностью может отскочить влево или вправо. Отклонение вправо и влево будет происходить совершенно по тем же законам, что и появление в рулетке красного и черного. На одну комбинацию лллллл… или пппппп… приходится множество комбинаций, состоящих из примерно равного числа отклонений влево и вправо. Поэтому чаще всего шарик будет попадать в среднюю пробирку и реже всего в самые крайние.

Можно провести большое число опытов, и каждый раз шарики будут распределяться примерно одинаково. Если усреднить результаты, то получим гладкую симметричную колоколообразную кривую, которая называется кривой Гаусса или кривой нормального распределения. Не кажется ли вам, читатель, странным, что какой‑то кривой мы уделяем так много внимания. На небольшом клочке бумаги можно начертить сколько угодно самых разнообразных кривых, и никому не придет в голову присваивать им имена или названия. А наша этой чести удостаивается. Почему? Не имеет ли она какой‑то математический признак, раз она заслужила специальное название.

Несомненно. Сейчас мы поясним, в чем состоит ее математическая общность, только разрешите от реального опыта перейти к абстрактной схеме. И пожалуйста, имейте в виду, что так поступают всегда физики‑теоретики, поэтому абстрагированием мы не нарушаем канонов науки.

Упрощение, которое мы введем, состоит в следующем: будем считать, что каждый столбик отличается от соседнего на единицу отклонений. Положим для конкретности, что доска состоит из 10 рядов препятствий. Будем считать, что шарик обязательно встречается с одним из препятствий каждого ряда и с равной вероятностью отскакивает вправо или влево, при этом отклонения происходят всегда на один интервал.

Тогда шарик, который попал в среднюю пробирку, отклонился 5 раз влево, 5 раз вправо. Следующая ячейка заполнена шариками, путь которых состоял из шести отклонений в одну сторону и четырех в другую. Далее идут пробирки, заполняющиеся шариками в соответствии с вариантами 7–3, 8–2, 9–1 и 10–0.

Вариант 5–5 осуществляется максимальным числом способов, 6–4 – уже несколько меньшим, 7–3 – еще меньшим… 10–0 – самая редкая комбинация. Отсюда и характерный вид кривой, проходящей через вершины столбиков.

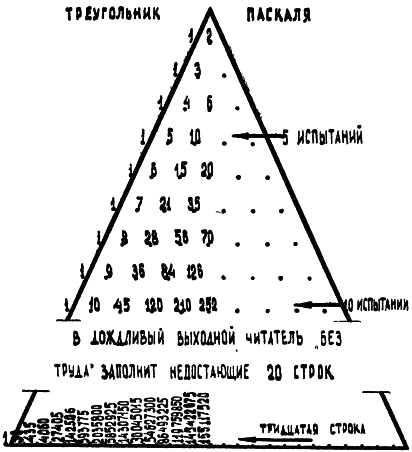
Высоты столбиков пропорциональны числу комбинаций, с помощью которых осуществляется тот или иной вариант. Об этом мы уже говорили (обратитесь, пожалуйста, к стр. 17) [ссылка], рассматривая все возможные варианты серии из 5 игр в рулетку.

Надо было бы для ясности выписать все комбинации для серии из 10 опытов. Пожалуй, мы пойдем на большее. На этой странице изображен так называемый треугольник Паскаля, с помощью которого можно определять числа комбинаций для любых рядов испытаний. Для того чтобы продолжить этот треугольник хоть до бесконечности, нужно лишь время и умение складывать. Даже таблицу умножения знать не обязательно, поскольку каждое число треугольника равно сумме двух чисел, а именно соседних левого и правого верхней строки.

В результате этих наипростейших арифметических операций мы получаем числа комбинаций левого и правого, красного и черного и вообще любых статистических «да» и «нет».

Как же пользоваться треугольником? Любая из его строк дает числа комбинаций для определенного числа элементов. На рисунке выделена пятая строка. Она отвечает на все вопросы, касающиеся рядов из пяти испытаний. Числам 1, 5, 10, 10, 5, 1 (мы помним их) пропорциональны вероятности появления красного цвета в пяти последовательных поворотах колеса рулетки 0 раз, 1 раз, 2 раза, 3 раза, 4 раза и 5 раз. Значение вероятностей мы получим, поделив каждое число треугольника Паскаля на общее число испытаний, которое равно сумме чисел строки.

Возвращаясь к доске Гальтона мы можем сказать, что при десяти случайных встречах с препятствиями число шариков, которые попадут в крайние пробирки (все встречи привели к одним лишь левым или к одним лишь правым отклонениям), будет в среднем в 252 раза меньше числа шариков, попавших в средний приемник.

С гауссовой кривой приходится сталкиваться во всех областях знания. Универсальность ее объясняется очень просто: на нее укладываются вероятности отклонений от среднего во всех случаях, если только отклонения «вправо» и «влево» равновероятны. Если же отклонения от среднего невелики, как это бывает очень часто, то подобное требование осуществляется всегда. Сейчас мы продолжим знакомство с этой замечательной кривой, лежащей в основе любой статистики.

Date: 2015-06-05; view: 557; Нарушение авторских прав