
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнение в полных дифференциалах
|
|
Уравнение
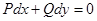
называется уравнением в полных дифференциалах, если
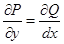 .
.
Уравнение
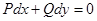
тогда и только тогда является уравнением в полных дифференциалах, когда существует функция 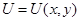 , такая, что
, такая, что
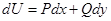 , то есть
, то есть 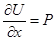 ,
, 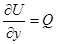
Общий интеграл уравнения
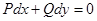
имеет вид 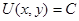
Пример. Решить дифференциальное уравнение
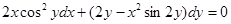
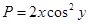 ,
, 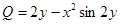
Проверим является ли данное уравнение уравнением в полных дифференциалах:
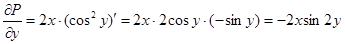 ,
,
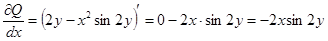 ,
,
то есть 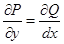 . Значит данное уравнение является уравнением в полных дифференциалах, то есть существует функция U, такая, что
. Значит данное уравнение является уравнением в полных дифференциалах, то есть существует функция U, такая, что
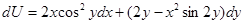 .
.
Поэтому
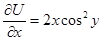 .
.
Отсюда
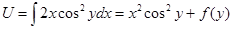 ,
,
где функция f(y) зависит только от y (постоянна по отношению к x).
Дифференцируя найденную функцию по y, получим выражение
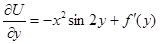 ,
,
которое, согласно
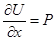 ,
, 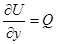 ,
,
можно приравнять к Q:
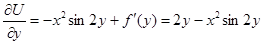
Отсюда 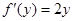 . Если уравнение в полных дифференциалах, то последнее выражение не будет зависеть от x.
. Если уравнение в полных дифференциалах, то последнее выражение не будет зависеть от x.
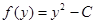
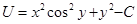
Окончательно получим:
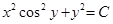
Уравнения n-го (второго) порядка, допускающие понижение порядка.
В некоторых частных случаях удаётся понизить порядок дифференциального уравнения второго или выше порядка. Зачастую оно в итоге приводится к дифференциальному уравнению первого порядка из рассмотренных ранее типов.
Дифференциальные уравнения вида y(n)=f(x)
Для решения дифференциального уравнения вида y(n)=f(x) сделаем замену
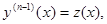
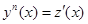
Тогда
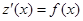 ,
,  ,
, 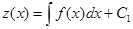
Но
 .
.
Следовательно,
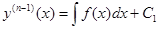 .
.
Повторяя эту операцию ещё (n-1) раз, получим y(x).
Пример. Решить дифференциальное уравнение 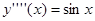 .
.
Проинтегрируем данное уравнение 4 раза:
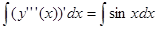 ,
,  ,
, 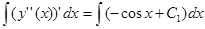 ,
,
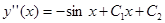 ,
,
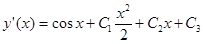 ,
,
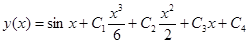 .
.
Дифференциальные уравнения, не содержащие явно искомой функции y.
Уравнения, не содержащие явно искомой функции y, имеют вид 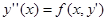 и сводятся к уравнению первого порядка с помощью замены
и сводятся к уравнению первого порядка с помощью замены 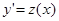 ,
, 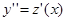 .
.
Пример. Решить дифференциальное уравнение
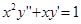 .
.
Сделаем замену 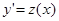 ,
, 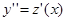 , получим
, получим
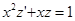
Уравнение второго порядка перешло в линейное уравнение первого порядка, которое можно решить с помощью замены
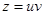 .
.
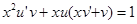
Приравняем выражение в скобках к нулю и найдём v:
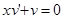
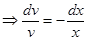
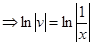
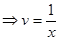
Подставим полученное выражение в уравнение
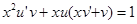
и получим:
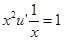 .
.
Найдём u:
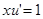
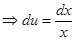
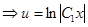
Тогда
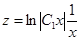 .
.
Следовательно
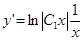 .
.
Найдём y:
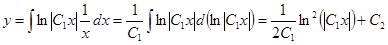
Дифференциальные уравнения, не содержащие явно независимой переменной x.
Уравнения, не содержащие явно независимой переменной x, имеют вид 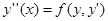 и сводятся к уравнению первого порядка с помощью замены
и сводятся к уравнению первого порядка с помощью замены 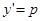 ,
, 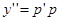 .
.
Пример. Решить дифференциальное уравнение
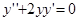 ,
,
если даны начальные условия 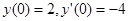 .
.
Сделаем замену 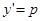 ,
, 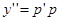 , получим
, получим
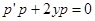
Уравнение второго порядка перешло в линейное уравнение первого порядка с разделяющимися переменными.
Найдём p:
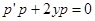
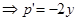
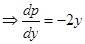
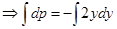
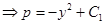
Следовательно,
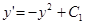 .
.
Подставим начальные условия 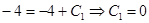 . Тогда
. Тогда
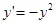 ,
, 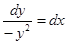 ,
, 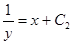 ,
, 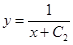
Подставим начальные условия 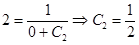 . Таким образом, частное решение имеет вид
. Таким образом, частное решение имеет вид
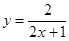 .
.
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами (ЛОДУ)
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
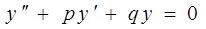
и решается с помощью составления характеристического уравнения:
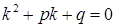 .
.
Формулы для нахождения общего решения однородного уравнения записаны в таблице:
| № | корни характеристического уравнения | общее решение однородного уравнения |
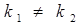 (корни действительные, различные) (корни действительные, различные)
| 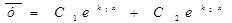
| |
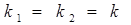 (корни действительные и равные) (корни действительные и равные)
| 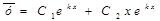
| |
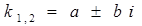 (корни комплексные сопряженные) (корни комплексные сопряженные)
| 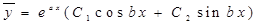
| |
| k1=k2=k (кратные комплексные сопряженные корни) | 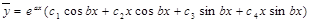
|
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами (ЛНДУ).
ЛНДУ имеет вид
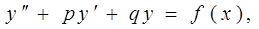
где p и q- действительные числа.
Решение неоднородного уравнения находиться по формуле:
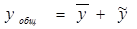 , где
, где
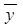 - решение ЛОДУ, а
- решение ЛОДУ, а 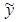 - частное решение ЛНДУ по виду правой части.
- частное решение ЛНДУ по виду правой части.
Формулы для нахождения частного решения 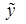 неоднородного уравнения по виду правой части
неоднородного уравнения по виду правой части 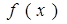 записаны в таблице:
записаны в таблице:
| № | Вид 
| Форма 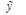
|
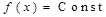
| 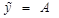 , если , если 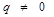 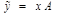 , если , если 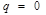
| |
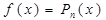 - многочлен - многочлен 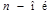 степени степени
| 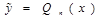 , если , если 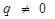 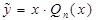 , если , если 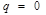
| |
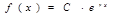 (произведение константы на показательную функцию) (произведение константы на показательную функцию)
| 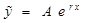 , если , если 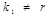 , , 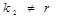 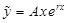 , если , если 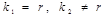 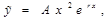 если если 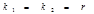
| |
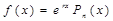 (произведение показательной функции на многочлен) (произведение показательной функции на многочлен)
| 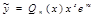 ; если r корень, то s его кратность; если нет, то s=0 ; если r корень, то s его кратность; если нет, то s=0
| |
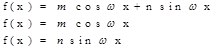
| 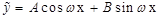 , если , если 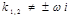 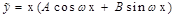 , если , если 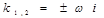
|
Неизвестные коэффициенты A, B, C отыскиваются методом неопределенных коэффициентов.
Пример. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
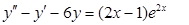
Общее решение данного уравнения находим в виде:
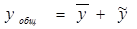
Найдем общее решение 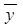 соответствующего однородного дифференциального уравнения
соответствующего однородного дифференциального уравнения
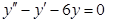
Для этого составим характеристическое уравнение:
k2 - k – 6 = 0.
Найдем его корни: k1 = -2; k2 = 3 – действительные и различные, поэтому общее решение имеет вид:
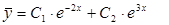 ,
,
где С1 и С2 – произвольные постоянные.
Найдем частное решение уравнения. Так как функция f(x) = (2x-1)e2x имеет вид Pn(x)eax, где Pn(x) = 2x -1 – многочлен 1-ой степени и a = 2 не является корнем характеристического уравнения, то частное решение уравнения запишем в виде:
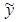 .= (Ax +B)e2x
.= (Ax +B)e2x
где А и В – коэффициенты, подлежащие определению. Воспользуемся методом неопределенных коэффициентов.
Найдем  и
и 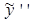
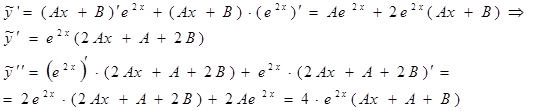
и подставим их в уравнение:
4е2х(Ах +А +В)- е2х(2Ах + А +2В)-6е2х(Ах + В) =(2х -1) е2х;
Поделим обе части уравнения на е2х:
4(Ах +А + В) - (2А + А + 2В) - 6(Ах +В) = 2х - 1 Þ
4Ах + 4А + 4В - 2Ах – А – 2В - 6Ах - 6В = 2х - 1 Þ
-4Ах+(3А-4В) = 2х-1 Þ - 4Ax = 2x; 3A- 4B= -1.
Откуда следует, что коэффициенты А и В должны удовлетворять, следующей системе уравнений:
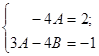
Решив ее, найдем А= -0,5; B= -0,125.
Подставим найденные значения А и В в уравнение 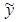 .= (Ax +B)e2x и найдем частное решение:
.= (Ax +B)e2x и найдем частное решение:
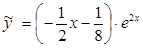
Следовательно, общее решение данного линейного неоднородного дифференциального уравнения второго порядка имеет вид:
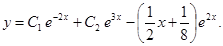
Date: 2015-06-05; view: 466; Нарушение авторских прав