Решение задач

А класс Геометрия

23.10.2014

Урок № 7

Тема урока:

Прямоугольник. Его свойства и признаки.

Записать в тетради число, тему урока

Повторение изученного

Повторить определения и свойства

Фронтальный опрос по теории

Вопросы:

1. Дайте определение прямоугольника.

2. Сформулируйте свойства прямоугольника.

3. Сформулируйте признаки прямоугольника.

4. Каким свойством обладает медиана прямоугольного треугольника, проведенная к гипотенузе?

5. Где расположен центр окружности, описанной около прямоугольного

треугольника?

Актуализация опорных знаний

устно решить задачи по рисункам

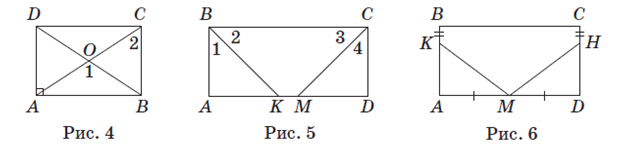
Задача 1. Дано: ABCD (рис. 4) — прямоугольник, ∠1= 120º.

Найти: ∠2. (Ответ: 60º.)

Задача 2. Дано: ABCD (рис. 5) — прямоугольник, ∠1 =∠2, ∠3 =∠4.

Доказать: BK = MC.

Задача 3. Дано: ABCD (рис. 6) — прямоугольник, BK = CH, AM = MD.

Доказать: KM = HM.

Закрепление усвоенных умений и навыков

Решение задач

Задача 1. В прямоугольнике биссектриса угла делит противолежащую сторону на отрезки 17 см и 8 см начиная от ближайшей

к этому углу вершины. Найдите периметр прямоугольника.

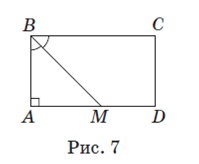
Решение

Пусть ABCD (рис. 7) — данный прямоугольник, BM — биссектриса угла B, AM =17 см, DM =8 см. Тогда ∠ ABM =∠ CBM =45º (BM — биссектриса). Значит, в прямоугольном треугольнике ABM

(∠ A =90º)∠ BMA =90º−45º=45º. Т.е. треугольник ABM —равнобедренный, AB = AM =17 см. По свойству противолежащих сторон прямоугольника CD = AB =17 см. DM =8 см (по условию), значит, AD = AM + MD =17 +8 =25 (см). BC = AD =25 см. Следовательно, P _ABCD =(AB +BC) ⋅2 =(17 +25)⋅2 =42⋅2 =84 (см).

Ответ: 84 см.

Задача 2. В прямоугольнике диагональ делит угол в отношении 1: 2, меньшая сторона прямоугольника равна 2,7 см. Найдите длины

диагоналей прямоугольника.

Решение

Пусть ABCD (рис. 8) — данный прямоугольник, BD — его диагональ, AB < BC, AB =2,7 см. Пусть ∠ CBD = x, тогда ∠ ABD =2 x. Т.к. ∠ ABC =90º,

то имеем: x +2 x =90º,

3 x =90º, Рис. 7

x =30º.

Значит, ∠ ABD =60º, ∠ CBD =30º. ∠ BDA =∠ BDC =30º как внутренние накрест лежащие при BC ǁ AD и секущей BD.

Таким образом, в треугольнике ABD, где ∠ A =90º, катет AB, лежащий против угла в 30º, равен половине гипотенузы: AB = BD.

Следовательно, BD =2 AB =2⋅2,7 =5,4 (см). Диагонали прямоугольника равны, то есть AC = BD =5,4 см.

Ответ: 5,4 см, 5,4 см.

Задача 3. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.

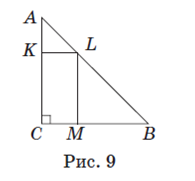
Решение

Пусть ABC (рис. 9) — данный прямоугольный треугольник, в котором ∠ C =90º, AC = CB =6 см, CKLM — прямоугольник. В треугольнике ABC ∠ A =∠ B =45º, т.к. этот треугольник равнобедренный.

Значит, в треугольнике AKL, где ∠ AKL =90º(т.к. CKLM —прямоугольник), тоже ∠ ALK= ∠ KAL =45º. Следовательно, треугольник AKL — равнобедренный, AK = KL. Аналогично в треугольнике LMB, где ∠ LMB =90º, ∠ MLB =∠ B =45º и LM = MB. Значит, CA = CK + KA = CK + KL =6 (см). Отсюда P _CKLM =(CK +KL) ⋅2=12 см.

Ответ: 12 см.

Задача 4. В прямоугольнике точка пересечения диагоналей находится от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Найдите стороны прямоугольника.

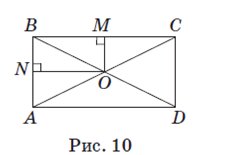
Решение

Пусть ABCD (рис. 10) — данный прямоугольник, точка O —точка пересечения его диагоналей. Проведем отрезки OM, перпендикулярный стороне BC, и ON, перпендикулярный стороне AB. Т.к. BC > AB, то ON на 4 см больше OM по условию. В треугольнике BOC BO = OC как половины равных диагоналей AC и BD. Значит, в треугольнике BOC высота OM является и медианой (свойство высоты равнобедренного треугольника, проведенной к основанию).

Т. е. BM = BC

Аналогично в треугольнике BOA (BO = OA) N — середина AB, BN = AB. Т.к. по условию PABCD =56 см, то AB + BC =28 (см), а BN + BM =28:2 =14 (см). Рассмотрим четырехугольник BMON, в нем три прямых угла, следовательно, BMON — прямоугольник по признаку. OM = BN = x см, тогда MB = ON =(x +4)

см. Значит, x + x +4 =14, 2 x =10, x =5. Итак, BN =5 см, значит, AB = CD =10 см, а BM =5+4 =9 см, BC + AD =18 см.

Ответ: 10 см, 10 см, 18 см, 18 см.

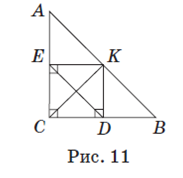
Задача 5. Гипотенуза AB прямоугольного треугольника ABC равна 8 см. Через середину гипотенузы — точку K проведены прямые, параллельные катетам треугольника и пересекающие их в точках D и E. Найдите длину отрезка DE.

Решение

В треугольнике ABC ∠ C =90º(рис. 11), так как AB по условию гипотенуза. В четырехугольнике CEKD по построению три угла прямые. Значит, CEKD — прямоугольник по признаку. Тогда диагонали DE и CK этого прямоугольника равны. Так как CK — медиана прямоугольного треугольника ABC (K — середина AB), то CK = AB= 4 см. Значит, DE =4 см.

Ответ: 4 см.

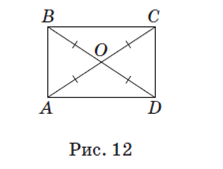
Задача 6. В прямоугольнике ABCD (рис. 12) точка O — точка пересечения его диагоналей, P _ABD -P _AOD =4 см. Найдите сторону AB.

Решение

P _{Δ ABD} =AB +BD +AD. P _{Δ AOD} =AO +OD +AD. AO = BO = OD как

половины диагоналей прямоугольника. P _ABD -P _AOD= AB +BD +AD -AO –OD- -AD=AB =4 (т.к. BD = BO + OD = AO + OD).

Ответ: 4 см.

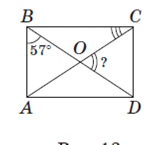
Задача 7. В прямоугольнике ABCD (рис. 13) точка O — точка пересечения диагоналей, ∠ ABD =57º. Найдите угол COD и докажите,что ∠ ABD +∠ BCA =90º.

C

Решение

Так как BO = AO как половины равных диагоналей прямоугольника

ABCD, то треугольник AOB — равнобедренный. Значит, ∠ BAO =∠ ABO =57º как углы при основании равнобедренного треугольника. Тогда ∠ AOB =180º−2⋅57º=180º−114º=66º. ∠ COD =∠ AOB =66º как вертикальные. Т.к. ∠ ABC =90º ABCD —прямоугольник), то ∠ CBD =90º−57º=33º. Треугольник BOC — равнобедренный с основанием BC, следовательно, ∠ BCA =∠ CBD =33º.

Значит, ∠ ABD +∠ BCA =90º, что и требовалось доказать.

Домашнее задание

1. В прямоугольнике ABCD точка O — точка пересечения диагоналей, ∠ AOD =70º. Найдите угол OCD.

2. Найдите угол между меньшей стороной и диагональю прямоугольника, если он на 30º меньше угла между диагоналями, лежащего против меньшей стороны.

3. Перпендикуляр, проведенный из вершины прямоугольника к диагонали, делит ее в отношении 3: 1. Найдите длину диагоналей прямоугольника, если точка пересечения диагоналей удалена от большей стороны на 6 см.