Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задачи для самопроверки. Задача. Две независимые случайные величины X и Y подчинены показательному закону распределения: X ~ E( )
|
|
Задача. Две независимые случайные величины X и Y подчинены показательному закону распределения: X ~ E(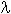
), Y ~ E(
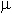). Написать выражение совместной плотности вероятности. Вычислить вероятность попадания случайной точки (X; Y) в квадрат с вершинами O (0;0), A (1;0), B (0;1), C (1;1).
Задача. Случайные величины X и Y независимы, причем: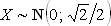 
, 
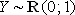. 1) Написать выражение совместной плотности вероятности. 2) Составить функцию распределения случайного вектора (X; Y). 3) Вычислить вероятность попадания случайной точки (X; Y) в область D = {| X | £ 1, | Y | £ 0,5}.
Задача. Найти ковариацию Kc, X, где X — некоторая случайная величина, а c — константа.
Задача. Известно, что следующие числовые характеристики некоторой случайной величины X: mX = 1,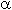 
2 = 2. Найти ковариацию KX,X.
Задача. Вычислить коэффициент корреляции 
и составить функцию распределения FX,Y (x,y) двумерного дискретного случайного вектора, закон распределения которого задан таблицей:
| X\Y | |||
| 0,5 | |||
| 0,25 | |||
| 0,125 | |||
| 0,125 |
Date: 2015-06-05; view: 475; Нарушение авторских прав