
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример 3
|
|
Составить уравнение параболы с вершиной в начале координат, если ее директриса параллельна оси Оу и проходит через левый фокус гиперболы:
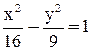 .
.
Определим координаты левого фокуса гиперболы: 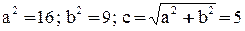 ,
, 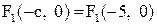 . Так как директриса параболы параллельна оси Оу и проходит через точку
. Так как директриса параболы параллельна оси Оу и проходит через точку  , то она имеет уравнение
, то она имеет уравнение 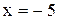 . Определим значение параметра р параболы:
. Определим значение параметра р параболы: 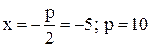 . Каноническое уравнение параболы имеет вид
. Каноническое уравнение параболы имеет вид 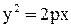 , т. е.
, т. е. 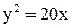 .
.
Контрольные варианты к задаче 3
1. Написать уравнение окружности, диаметром которой служит отрезок, отсекаемый на оси Ох параболой 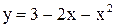 .
.
2. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом 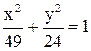 , при условии, что эксцентриситет ее равен 5/4.
, при условии, что эксцентриситет ее равен 5/4.
3. Найти точки пересечения асимптот гиперболы 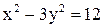 с окружностью,
с окружностью,
имеющей центр в правом фокусе гиперболы и проходящей через начало координат
4. Найти длину и уравнение перпендикуляра, опущенного из фокуса параболы 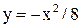 на прямую, отсекающую на осях координат отрезки
на прямую, отсекающую на осях координат отрезки 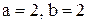 .
.
5. Составить уравнение множества точек, равноудаленных от точки 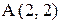 и оси абсцисс. Построить чертеж.
и оси абсцисс. Построить чертеж.
6. Дан эллипс 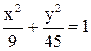 . Составить уравнение гиперболы, имеющей фокусы,
. Составить уравнение гиперболы, имеющей фокусы,
общие с фокусами эллипса, если известно, что эксцентриситет гиперболы равен 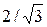 .
.
7. Составить уравнение окружности, проходящей через фокусы эллипса 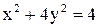 и имеющей центр в его «верхней» вершине.
и имеющей центр в его «верхней» вершине.
8. Составить уравнение окружности, диаметром которой служит отрезок, отсекаемый на оси Ох параболой 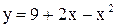 .
.
9. Построить эллипс 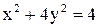 и параболу
и параболу 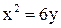 и найти площадь трапеции, основаниями которой служат большая ось эллипса и общая хорда эллипса и параболы.
и найти площадь трапеции, основаниями которой служат большая ось эллипса и общая хорда эллипса и параболы.
10. Написать уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 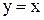 и окружности
и окружности 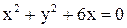 и симметрична относительно оси Ох.
и симметрична относительно оси Ох.
11. Дан эллипс 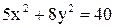 . Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы - в вершинах данного эллипса.
. Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы - в вершинах данного эллипса.
12. Составить уравнение окружности, имеющей центр в фокусе параболы 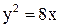 и касающейся ее директрисы. Найти точки пересечения параболы и окружности.
и касающейся ее директрисы. Найти точки пересечения параболы и окружности.
13. Составить уравнение окружности, диаметром которой служит отрезок, отсекаемый параболой 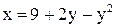 на оси Оу.
на оси Оу.
14. Составить уравнение окружности, диаметром которой служит отрезок, отсекаемый на оси Оу параболой 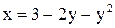 .
.
15. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом
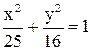 , при условии, что эксцентриситет её равен 5/4.
, при условии, что эксцентриситет её равен 5/4.
16. Фокус параболы совпадает с центром окружности 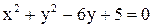 , а вершина параболы лежит в начале координат. Составить уравнение параболы и ее директрисы.
, а вершина параболы лежит в начале координат. Составить уравнение параболы и ее директрисы.
17. Написать уравнение окружности, проходящей через фокусы эллипса 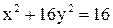 и имеющей центр в его «нижней» вершине.
и имеющей центр в его «нижней» вершине.
18. Дан эллипс 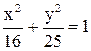 . Составить уравнение гиперболы, если ее фокусы совпадают с вершинами эллипса, а ее вершины – с фокусами эллипса.
. Составить уравнение гиперболы, если ее фокусы совпадают с вершинами эллипса, а ее вершины – с фокусами эллипса.
19. Составить уравнение параболы с вершиной в начале координат, если ее директриса параллельна оси Ох и проходит через «верхний» конец малой оси эллипса 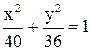 .
.
20. На параболе 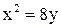 найти точку, расстояние которой до фокуса равно четырем.
найти точку, расстояние которой до фокуса равно четырем.
21. На параболе 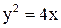 найти точку, расстояние которой до фокуса равно
найти точку, расстояние которой до фокуса равно
пяти.
22. Вершина параболы лежит в начале координат, директриса ее проходит через «правый» фокус эллипса 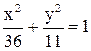 . Составить уравнение параболы.
. Составить уравнение параболы.
23. На прямой 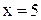 найти точку, одинаково удаленную от «левого» фокуса и «верхней» вершины эллипса
найти точку, одинаково удаленную от «левого» фокуса и «верхней» вершины эллипса 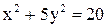 .
.
24. Дано уравнение гиперболы 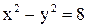 . Составить уравнение эллипса, имеющего с гиперболой общие фокусы и проходящего через точку
. Составить уравнение эллипса, имеющего с гиперболой общие фокусы и проходящего через точку 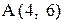 .
.
25. Составить уравнение окружности, диаметром которой служит отрезок пря-
мой 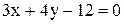 , заключенный между осями координат.
, заключенный между осями координат.
26. Через вершину параболы 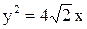 проведена прямая под углом
проведена прямая под углом 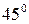 к оси Ох. Вычислить длину хорды, отсекаемой параболой на этой прямой.
к оси Ох. Вычислить длину хорды, отсекаемой параболой на этой прямой.
27. Эллипс, симметричный относительно осей координат, проходит через точку 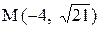 и имеет эксцентриситет
и имеет эксцентриситет 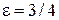 . Написать простейшие уравнение эллипса и найти расстояния от точки М до фокусов.
. Написать простейшие уравнение эллипса и найти расстояния от точки М до фокусов.
28. Даны вершины треугольника АСВ: 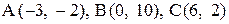 . Составить уравнение окружности, для которой медиана АЕ служит диаметром.
. Составить уравнение окружности, для которой медиана АЕ служит диаметром.
29. Найти эксцентриситет и уравнение асимптот гиперболы, фокусы которой находятся в вершинах эллипса 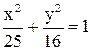 , если произведение эксцентриситетов гиперболы и эллипса равно единице.
, если произведение эксцентриситетов гиперболы и эллипса равно единице.
30. Составить каноническое уравнение эллипса, проходящего через точки 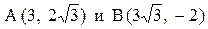 . Найти фокусы и точки пересечения эллипса и окружности, центр которой находится в начале координат и радиус равен
. Найти фокусы и точки пересечения эллипса и окружности, центр которой находится в начале координат и радиус равен 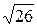 .
.
Date: 2015-04-23; view: 1931; Нарушение авторских прав