Принципы и методы имитационного моделирования

Остановимся теперь на применении имитационного моделирования.

Создание имитационной модели этапируется следующим образом:

- структуризация объекта моделирования;

- формирование сценария функционирования объекта моделирования;

- выбор из числа известных или создание нового метода имитационного моделирования;

- разработка общей структуры имитационной модели;

- разработка общей схемы функционирования имитационной модели;

- реализация блоков имитационной модели.

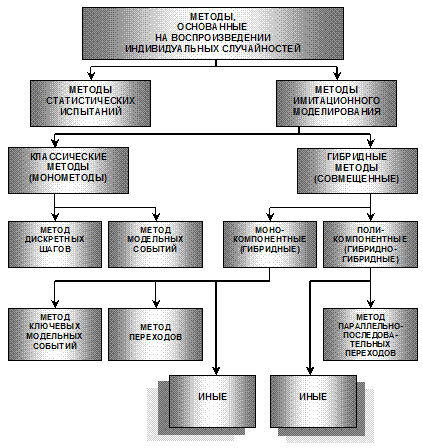
В настоящее время известно несколько методов математического моделирования, основанных на воспроизведении случайных событий и процессов и относимых к категории методов имитационного моделирования (см. рис. 2.1).

Так называемые методы статистических испытаний занимают промежуточное положение между аналитическими и имитационными методами, поэтому они выделены в самостоятельный класс. Базовым классификационным (дискриминирующим) признаком разделения методов, приведенных на указанном рисунке, служит способ «продвижения» по модельному времени.

В методах статистических испытаний указанного «продвижения» как такового нет.

Действительно, пусть модель представлена в виде:

_ _ _

Y = F(X, Z),

_ _ _

где Y, X и Z – случайные величины, а F – некоторое заранее заданное аналитическое соотношение (зависимость).

Тогда при решении уравнения со случайными входами и параметрами несколько раз генерируются реализации случайных величин X и Z в порядке вычислений, определенных F, и тем самым находятся реализации Y, которые затем, как правило, осредняются. Зависимости F могут быть сложными.

Значения функционалов иногда также целесообразно оценивать с помощью метода статистических испытаний.

Например, если требуется вычислить:

Y = ,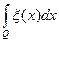

Рис. 2.1. Методы имитационного моделирования

то подбирается такое распределение некоторой случайной величины Z, при котором выполняется условие:

Y = M{Z} = ,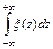

а затем генерируются реализации случайной величины Z, выборочный момент которых является эффективной, состоятельной и несмещенной оценкой искомого значения Y.

Перейдем теперь собственно к методам имитационного моделирования, рассматривая их последовательно.

Метод дискретных шагов (называемый также методом продвижения на Dt, просто методом Dt, методом временного шага и т.д.) заключается в том, что модельное время «продвигается» на каждой итерации на определенный промежуток, а затем проверяется, какие за этот промежуток совершились события, закончились процессы, то есть воспроизводится изменение состояния по схеме «продвинулся по времени, подвел итоги по состоянию». Этот метод наиболее распространен, так как относительно быстр и прост, содержит ряд элементов аналитического описания, удобен для представления в технической документации. Его недостатки: не всегда достигается требуемая адекватность, при отказе от серьезных предположений нарушаются синхронность и причинно-следственные связи между событиями и процессами. В результате приходится делать величину временного шага исчезающе малой, сводя на нет главное преимущество этого метода – скорость счета.

Как следствие, имитационные модели, базирующиеся на методе дискретных шагов, описывают либо объекты со слабо связанными фрагментами (распараллеленные подпроцессы), либо объекты с неравной «прозрачностью», особо детализируя один из фрагментов. Искомые показатели состояния оцениваются только в моменты времени, приходящиеся на заранее определенные точки, совпадающие с дискретными точками модельного времени, в которых производится изменение состояния. Трассировки при повторных имитационных экспериментах, как правило, порождают выборки с однородной дисперсией, что позволяет определять требуемое число повторных реализаций имитационного эксперимента. Задание ненулевых начальных условий не создает каких-либо серьезных проблем, внешние начальные условия обычно не требуют пересчета во внутренние (машинные, модельные).

Самая простая и поэтому часто реализуемая разновидность метода дискретных шагов – метод фиксированного шага, когда дискретные шаги (или, скорее, моменты) t_j и t_j+1 отстоят друг от друга на постоянную величину модельного времени:

t_j+1 - t_j = const; j Î [1,N].

Реже применяется метод вложенных дискретных шагов, для которого
t_j+1 - t_j ¹ const, и, как правило:

t_j+1 - t_j = const; j Î J; j £ N,

t_k+1 – t_k = const; k Î K; k £ K,

или просто задано множество {t₁,..., t_N} и не наложены ограничения на
t_v+1 – t_v.

Если {t₁,..., t_N} жестко зафиксировано перед началом имитационного эксперимента тем или иным из названных способов, то это указывает на применение метода вложенных дискретных шагов с априорным квантованием.

Практически не встречается ситуация, когда, дойдя методом дискретных шагов до момента t_m с шагом D₁, необходимо вернуться к моменту t_m-1 и идти вперед с шагом D₂< D₁ до t_m или даже дальше. В этом случае речь идет об использовании метода вложенных дискретных шагов с повторным проходом. Главная трудность здесь – вернуть состояние модели из t_m в t_m-1 (UNDO -проблема или проблема манипуляционного отката).

Метод модельных событий (называемый также методом продвижения на DS, просто методом DS, методом шага по событиям и т.д.) состоит в том, что модельное время «продвигается» на промежуток, соответствующий по продолжительности модельному времени до наступления ближайшего события или завершения процесса, а затем изменяется модельное состояние и планируются или перепланируются (по составу и времени наступления) события, которые должны произойти в будущем, как это определялось на предыдущих шагах (то есть воспроизводится изменение состояния по схеме «дошел до события, изменил состояние, спланировал или перепланировал будущие события»). Достоинства данного метода: обеспечивает высокую адекватность, реализуется проще, чем метод дискретных шагов, проблема синхронизации решена автоматически. Существенным недостатком является длительное время счета, которое катастрофически растет прежде всего с увеличением числа элементов объекта моделирования (в частности, парков изделий). По сравнению с методом дискретных шагов этот метод потенциально позволяет больше детализировать моделируемые объекты, учитывать разного рода ограничения, нестационарности, случайные факторы, а также взаимосвязи. Степень «прозрачности» фрагментов можно задавать, исходя только из необходимой точности, трудоемкости разработки, располагаемых ресурсов и вычислительных средств.

Наблюдаемые показатели состояния могут оцениваться с произвольной дискретностью, причем индивидуальной для каждого из них. Благодаря точному описанию возникают расслоенные выборки и выборки с неоднородными дисперсиями оценок показателей состояния. Оценить в этом случае требуемое число повторных реализаций имитационного эксперимента не удается из-за больших затрат машинного времени. Приходится обходиться тем их количеством, которое укладывается в лимит машинного времени, а затем находить статистические характеристики выборки. Задание ненулевых начальных условий требует специального адаптера – блока формирования модельных начальных условий, так как внешние начальные условия определяются «от события» (уже производится..., уже ремонтируется...), а внутренние, модельные требуют задания «до события» (перестанет эксплуатироваться..., завершится ремонт...). Как правило, этот адаптер использует часть модулей самой модели и трудоемкость его создания составляет 2–7% от общей трудоемкости разработки имитационной модели и ее программной реализации.

При рассмотрении всех событий говорят о методе возникающих событий; если же исследуются только те, которые совпадают во времени и(или) пространстве, то это значит, что применяется метод совпадающих событий.

Чисто имитационные модели за небольшим исключением на практике не встречаются. В той или иной форме они обязательно сопряжены с аналитическими моделями. Действительно, исходные данные – это, по существу, те же аналитические модели, заданные численно (например, динамика производственных возможностей, надежность изделий и т.д.). В том случае, если они не зависят от имитируемых событий и процессов, принято говорить о так называемых моделях внешней динамики.

Противоречивые преимущества и недостатки рассмотренных известных методов имитационного моделирования не позволяют строить имитационные модели, которые обладали бы одновременно высокими характеристиками адекватности, универсальности, реактивности, открытости, а также требовали бы приемлемых вычислительных ресурсов – в частности, объемов оперативного запоминающего устройства (ОЗУ/RAM) и внешнего запоминающего устройства (ВЗУ/HDD).

Действительно, перечисленные характеристики моделей и их программных реализаций являются заведомо конкурирующими, конфликтующими. Кроме того, в дополнение к перечисленным добавляется также и стоимостная характеристика – затраты на разработку соответствующего программного продукта. Вследствие чего должна ставиться и решаться задача оптимизации проектного решения в отношении модели и в конечном счете конечнопользовательского программного продукта – задача выбора метода имитационного моделирования. Естественно, что это осуществимо только посредством выполнения комплексного технико-экономического обоснования.

В рамках традиционно применяемых и уже упоминавшихся метода дискретных шагов и метода модельных событий рассматриваемая задача сводится к векторной оптимизационной, которая чаще всего применительно к рассматриваемой предметной области имеет либо слишком низкоэффективное решение, либо не имеет допустимого решения вообще. В самом деле, например, уменьшая интервал дискретности для метода дискретных шагов, в пределе его можно теоретически свести фактически к методу модельных событий. Выиграв при этом в точности (дойдя по точности до соответствующей методу модельных событий), придется неприемлемо сильно увеличить вычислительную ресурсоемкость, которая будет заведомо не меньшей, чем в том случае, если бы был применен сам этот метод модельных событий.

Скорее всего (хотя строгого доказательства справедливости этого утверждения получить пока не удалось), применительно к рассматриваемой области моделирования ни один из перечисленных выше двух методов ни в одной из их обсуждавшихся разновидностей принципиально не может обеспечить приемлемой технико-экономической эффективности управления. Из этой констатации следует, что задача оптимального анализа не имеет продуктивного разрешения и необходимо решать задачу оптимального синтеза – т.е. разработки нового метода имитационного моделирования.

Последняя, в свою очередь, декомпозируется на подзадачу выбора исходной схемы (включая исследование ее существования) и подзадачу разработки собственно самого нового метода имитационного моделирования. Вполне естественное при этом требование обеспечения сочетания достоинств методов дискретных шагов и модельных событий и взаимопогашение (абсолютное или частичное) их недостатков, т.е. создание гибридного метода имитационного моделирования.

Таким образом, необходимо и достаточно рассматривать такую версию способа формирования системы модельного инструментария, как ее расширение. С учетом того, что применительно к сфере маркетинговых операций требование адекватности является приоритетным, целесообразно выбрать в качестве отправного, базисного метод модельных событий.

Целевой направленности и содержанию сформулированной задачи синтеза не противоречит ее версия, предусматривающая обоснование введения процедуры обработки модельных событий, которая, с одной стороны, не ухудшила бы точностных характеристик модели, а, с другой стороны, резко бы сократила потребление вычислительных ресурсов (прежде всего временных) при проведении компьютерных экспериментов.

Анализ затрат процессорного времени для случая применения метода модельных событий показывает, что очень значительное машинное время расходуется, во-первых, на диспетчеризацию модельных событий, и, во-вторых, на передачу обработочного управления элементам иерархической системы программной реализации – прежде всего подпрограммам (в силу длительности операций ОС со стеками).

Кроме того, расширение типажа непосредственно диспетчеризуемых модельных событий неприемлемо обогащает и тем самым резко усложняет модельное описание. Даже если соответствующий модельный и программный аппарат является приниципиально реализуемым, он, тем не менее, становится чрезмерно дорогостоящим в части его разработки.

Таким образом, искомая процедура должна быть направлена на минимизацию номенклатуры диспетчеризуемых модельных событий.

Единственным решением при таком подходе, насколько это удалось установить на основе логического анализа, является переход от индивидуальных модельных событий к специально сформированным их группам (кортежам), подлежащим диспетчеризации и обработке. Иными словами, должен быть реализован переход от ординарного потока модельных событий к ординарному потоку некоторым образом организованных кортежей модельных событий, причем модельные события каждого кортежа являются условно скомпрессированными в единый момент времени.

Такой метод, основанный на формировании кортежей модельных событий и их последующей обработке в процессе модельного эксперимента, был назван методом ключевых модельных событий. Следует отметить, что доказательств его единственности или превалирования по эффективности над другими потенциально существующими процедурами не искалось и получено не было. Однако он удовлетворяет условиям сформулированной задачи разработки гибридного метода и дает хороший реальный эффективностный выигрыш по сравнению с традиционными методами дискретных шагов и модельных событий.

Рассмотрим, в чем заключается этот гибридный метод ключевых модельных событий.

По отношению к сложным объектам, для которых строятся имитационные модели состояния на базе метода модельных событий, был установлен ряд важных особенностей.

Пусть модельные события расположены в хронологической последовательности их наступления с учетом причинно-следственных связей: R₁,..., R_x. Эта последовательность обладает следующими свойствами:

1) Любому из ее элементов присуща сложная, имеющая вероятностный характер, зависимость вида:

R_v = R_v (R_v-1,..., R₁, H), v>1,

где H – параметры объекта моделирования, отраженные в имитационной модели.

2) Последовательность включает подпоследовательности, элементы которых íR_g,..., R_g+lwý = íR^w₁,..., R^w_lwý допускает объединение по признаку:

T(R^w₁) =... = T(R^w_lw),

но R^w_g+1, с точки зрения причинно-следственной связи, следует за R^w_g, где g – номер произвольного события, а

T(R_g+lw+1) > T(R_g+lw), g + 1 < x,

где T(R) – момент наступления модельного события R.

3) Все таким образом выделенные подпоследовательности могут быть разделены на m групп, в пределах каждой из которых элементы соответствующей подпоследовательности не образуют инверсий по своему содержанию, т.е. выделяется кортеж, названный схемой следования модельных событий íS^k₁,..., S^k_lký, kÎ [ 1,m ], характерная для каждой из таких групп. Устойчивость соответствия схеме следования проявляется в том, что ведущее событие группы присутствует всегда, а наличие или отсутствие других элементов подпоследовательности обусловлено состоянием объекта моделирования и реализацией отражаемых в имитационной модели разного рода случайных величин. При этом каждое из íS^k₁ý, kÎ [ 1,m ] (именно они и названы ключевыми модельными событиями) отвечает либо поступлению входных воздействий на локальный подобъект, например, представленный в виде системы массового обслуживания (СМО), либо возникновению реакции на выходе, либо уничтожению сигнала в локальной СМО, либо наступлению момента измерения или варьирования параметров и структуры. Первые три ситуации соответствуют поступлению требования на вход, окончанию обслуживания требования или его потере из-за превышения ограничения на время пребывания, времени ожидания (могут быть и другие причины).

Выделенные ситуации задают процедуру генерации кортежей. Таким образом, в этом новом методе очередное «продвижение» модельного времени производится на шаг, отвечающий наступлению очередного (ближайшего по времени появления), но ведущего модельного события, либо некоторому дискретному моменту.

В данном случае íS^k₁ý, kÎ [ 1,m ] отражает одну из следующих ситуаций:

- поступление требований на вход локальной СМО;

- завершение обслуживания в локальной СМО или ее фазе (для матричной СМО - каналов, связанных с приоритетными требованиями);

- истечение допустимого срока пребывания требований в очереди;

- наступление момента измерений или варьирования параметров и структуры (т.е. реализация тактовых событий).

Этот метод включает в качестве частного случая и концепцию кусочно-линейного автомата.

Оценка наблюдаемых показателей состояния может быть реализована одним из двух способов:

- методом синхронного расчета показателей состояния или подбора элементов выборки для их последующего вынесенного расчета;

- методом апостериорного анализа трассировки наблюдавшихся состояний (например, протокола имитационного эксперимента).

Второй метод позволяет не только оценивать показатели состояния, но и анализировать причины возникновения тех или иных неординарных ситуаций. Однако он требует архивации огромных файлов и пригоден лишь для относительно несложных вариантов, так как для анализа сложных ситуаций DEBUG -трассировка (отладочная трассировка) недостаточна, а нужен нестереотипный разрез или полный DUMP (полный протокол) имитационного эксперимента, который физически невозможно размещать на внешних носителях, не говоря уже о манипуляциях с ними. Поэтому, как правило, пользуются методом синхронного расчета показателей состояния.

Для оценки наблюдаемых показателей состояния при применении метода модельных ключевых событий используют один из трех способов:

- регистрационный (для каждого дискретного момента времени и произвольной реализации имитационного эксперимента показателем состояния является значение рабочей переменной имитационной модели);

- логический (искомое значение показателя состояния находят в результате логического анализа имеющегося в данный момент календарного модельного времени содержания банка состояний имитационной модели);

- оценочный (рассчитываемый показатель состояния определяется как некоторая статистическая оценка по наблюдавшейся выборке событий или реализаций случайной величины).

Таким образом, с помощью метода ключевых модельных событий удается построить имитационную модель более сложную, чем это возможно при использовании метода дискретных шагов, и по быстродействию на один-два порядка превосходящую модель, которую позволяет создать традиционный метод модельных событий.

Этот метод дает возможность строить модели замкнутого контура управления за счет введения синхронизации и взаимосвязей с моделями внешней динамики, а также организовывать интерактивные процедуры.

Для обеспечения полной инвариантности разработанной имитационной модели по отношению к тому, какая модель внешней динамики используется, задание последней в исходных данных организовано так, что оно соответствует кусочно-постоянной аппроксимации развертки во времени переменных, определяющих эту внешнюю динамику.

Правило останова функционирования имитационной модели обычно принимается стереотипным. Имитационный эксперимент прекращается, если выполняется хотя бы одно из следующих условий:

- исчерпан выделенный лимит компьютерного времени или допустимое время ожидания пользователя;

- реализованы для заданного интервала имитации все повторные реализации;

- произошел выход вычислительного эксперимента на невоспроизводимую имитационной моделью экстремальную ситуацию.

В отдельных случаях ориентируются на приостанов или останов вычислений при выполнении заранее заданного экспериментатором некоторого содержательного условия (так называемые BREAKPOINT-условия или условия приостанова).

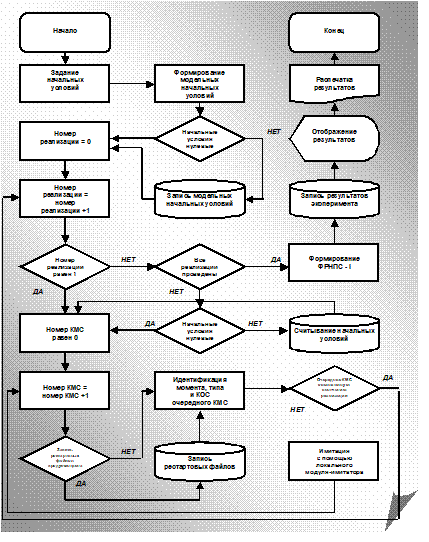
Структура имитационной модели на базе метода ключевых модельных событий имеет вид, показанный на рис. 2.2. Для идентификации каждого типа ключевых модельных событий введен перечень реквизитов, содержание которых полностью обусловливает последствия этих событий с учетом знания в данный момент всего состояния объекта моделирования. Эти реквизиты составляют код описания ключевого модельного события (КОС). Эта структура имитационной модели является топологически типовой.

Имитационная модель рассматриваемого типа функционируют следующим образом (см. рис. 2.3).

Первоначально задаются начальные условия. Затем формируются модельные начальные условия путем начальной установки банка состояний, представляющего собой совокупность файлов, которые позволяют для каждого момента модельного календарного времени:

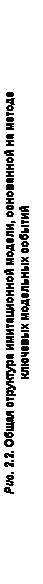Рис. 2.3. Блок-схема функционирования имитационной модели на базе метода ключевых модельных событий

- фиксировать моменты наступления очередных (будущих) ключевых модельных событий и их КОС, насколько это обусловлено для каждого текущего момента модельного календарного времени;

- идентифицировать состояние и характеристики объекта моделирования.

После этого производится заданное число повторных реализаций имитационного эксперимента. Для любой из них и произвольного момента календарного модельного времени на интервале имитации с помощью модуля-диспетчера осуществляется идентификация очередного ключевого модельного события из числа описанных в банке будущих ключевых модельных событий: момент его наступления t (ключевой модельный момент); тип ключевого модельного события r; КОС.

Такая диспетчеризация проводится исходя из того, что в некоторый момент времени выбирается и объявляется очередным то ключевое модельное событие, которое должно произойти в ближайшее к этому моменту время.

По найденному r – типу очередного ключевого модельного события – устанавливается локальный модуль-имитатор, к которому происходит переход. Этот модуль-имитатор представляет собой алгоритм, описывающий соответствующую схему следования S^r_l,..., S^r_lr. При обращении в r -ому локальному модулю-имитатору используются следующие данные: момент наступления ключевого модельного события t; банк состояний в априорном по отношению к данному вхождению в данный локальный модуль-имитатор состояний; КОС.

В общем случае в процессе имитации согласно схеме следования S^r_l,..., S^r_lr разыгрываются моменты будущих ключевых модельных событий и определяются их КОС. Некоторые из ключевых модельных событий, запланированные в предыдущие моменты времени, отменяются, а также разыгрываются в рамках вероятностных механизмов или исчисляются на основе детерминированных схем исходы модельных событий, не являющихся ключевыми. При этом соответствующие изменения производятся в банке состояний, кро­ме того, может пополняться файл регистрации наблюдаемых переменных состояний (ФРНПС) третьего уровня – ФРНПС-III. Локальные блоки-имитаторы и схема следования построены так, чтобы реализовать максимум возможных для момента t модельных событий и определить (в том числе переопределить и отменить), возможно, больше ключевых модельных событий на будущее.

В частном случае, если очередное ключевое модельное событие соответствует наблюдению за некоторой компонентой показателя состояния, то происходит ее вычисление. Элемент ФРНПС-II может формироваться одним из трех указанных ранее способов. Выбор способа зависит от содержания компоненты показателя состояния и дискретности ее оценки.

Через определенное число ключевых модельных событий всех или одного типа рестартовые файлы можно архивировать.

По завершении имитационного эксперимента получают:

- суммарное количество реализовавшихся (наблюдавшихся) ключевых модельных событий;

- калькуляцию суммарных затрат по статьям;

- результаты обработки множества реализаций наблюдаемых переменных состояния – оценку среднего каждой из наблюдаемых пе­ременных состояния по множеству повторных реализаций имитационного эксперимента, оценку среднего квадратического отклонения, минимальное и максимальное из реализовавшихся значений. Эти результаты и составляют ФРНПС-I.

Первые два вида результатов обязательны и выдаются для каждой из реализаций имитационного эксперимента.

Наблюдаемые показатели состояния – программируемые. Кроме того, при имитационном эксперименте предусматривается возможность получения протокола имитационного эксперимента, оценки наблюдаемых переменных состояния для множества всех повторных реализаций имитационного эксперимента, а также состояния элементов банка состояний, отражающих занятость локальных СМО.

Рассмотрим второй гибридный метод имитационного моделирования – метод переходов.

При его построении предлагается использовать своего рода «отраженный» метод ключевых модельных событий (условно названный методом переходов), где за основу принят метод дискретных шагов, а метод модельных событий представлен типовыми кортежами кортежей стереотипных событий-трансформаций.

При этом предлагается принять за основу метод дискретных шагов, а метод модельных событий представлен типовыми кортежами кортежей стереотипных событий-трансформаций.

Формально метод переходов предполагает следующую методологическую формализацию:

- рассматривается трансформация состояния материальных квантов, число состояний которых конечно и априорно фиксировано, причем трансформации могут протекать только в дискретные моменты времени. Каждое из состояний соответствует нахождению материального кванта внутри одного из фиксированных подобъектов и маршрут его перехода в другой подобъект задан некоторым жестким вероятностным правилом, которое может срабатывать только в дискретные моменты времени. Таким образом, формируется некоторое множество состояний материального кванта S₁,..., S_n, для которого назначается матрица вероятностных правил переходов ((R_ij)), задающая правило перехода материального кванта из состояния (подобъекта) i в состояние (подобъект) j. Посредством конструирования элементов матрицы ((R_ij)) некоторые состояния можно сделать недостижимыми для материальных квантов, а некоторые – поглощающими или же, наоборот, генерирующими;

- рассматривается динамика параметров внешней и внутренней среды, которые могут изменяться только в дискретные моменты времени (т.е. соответствующие функции, их задающие, являются кусочно-постоянными) и параметрировать ((R_ij));

- при формировании матрицы ((R_ij)) устанавливается множество типовых начальных состояний материальных квантов для произвольного момента времени, которое соответствует подобъектам-донорам;

- для каждого из этих состояний формируется ветвящийся вероятностный маршрут следования материального кванта к подобъекту-реципиенту.

При этом в нашем случае множества подобъектов-доноров и подобъектов-реципиентов тождественны и ((R_kk)) – непустые правила (т.е. материальный квант может перейти в тот же подобъект, т.е. остаться в нем).

Интересно отметить, что интерпретацию предложенного метода можно осуществить в различных глоссариях, соответствующих различным научным дисциплинам.

В частности, можно использовать предельные и обычные варианты:

- теории вероятностей, в рамках которых предусматривается выделение матриц вероятностных переходов, но где вероятности не заданы численно и не обязаны нормироваться в общепринятом понимании (т.е. доказательство полногруппности вариантов перехода очевидно, а оценка их вероятностей может быть просто неосуществимой или некорректной по смыслу);

- теории массового обслуживания, которая интерпретирует подобъекты как локальные системы массового обслуживания, а материальные кванты – как требования;

- теория предикатов и конечных автоматов;

- стохастические сети с детерминированными вершинами и динамическими вероятностными дугами и т.д.

Однако, в силу того, что такое отнесение не является прагматически необходимым, не будем жестко отождествлять предложенный метод имитационной идентификации с известным инструментарием исследования операций.

Таким образом, метод переходов состоит в пошаговом продвижении по модельному времени с трансформацией нахождения каждого из материальных квантов в одном из подобъектов.

Необходимая точность при этом достигается за счет минимизации квантования шкалы модельного времени – теоретически она может быть сделана сколь угодно малой, но ограниченной, исходя из требований по реактивности управляющей системы и соответственно времени компьютерной имитации.

Метод переходов в общем случае предполагает, что адресация попадания материального кванта зависит от:

- состояния материального кванта в предшествующий и более ранние моменты;

- параметров в предшествующий и более ранние моменты;

- параметров в последующий момент.

То есть формально при имитации должна возникать система с неограниченной памятью, а также зависимостью от будущей динамики.

Такое положение дел серьезно осложняет модельное исполнение имитационной модели. Поэтому во многих практически важных случаях, в том числе в данном, возможно в условиях некоторых предположений приемлемой жесткости свести описание к модели с памятью на один шаг назад, когда ретроспективный период может быть ограничен одним дискретным шагом назад, т.е. для момента времени t это будут соответственно момент t-1 и интервал [ t-1,t ].

Поэтому достаточно сформировать вероятностные маршруты только «исходящих» материальных квантов.

Метод переходов ориентирует также на то, что оценивание показателей состояния для момента t производится по интервалу [ t-1,t) и требует сначала оценки показателей состояния, а уже потом – трансформации состояния материальных квантов. В противном случае для обеспечения наблюдаемости моделируемых процессов либо придется формировать протокол имитационного эксперимента и конструировать эвристические процедуры его интерпретации, либо сохранять информацию обо всем развитии событий. Во всех случаях это увеличивает вычислительную ресурсоемкость имитационных экспериментов в части объема потребляемой компьютерной памяти и скорости вычислений.

Соответствующие имитационные модели на базе метода переходов имеют структурный вид, представленный на рис. 2.4.

Функциональное назначение блоков такой имитационной модели следующее.

Блок формирования модельных начальных условий обеспечивает преобразование заданных начальных условий в модельное представление – своего рода трансляцию.

Существенной особенностью создаваемой на основе метода переходов имитационной модели является то, что для нее существенно облегчена процедура формирования модельных начальных условий, т.к. и внешние и модельные начальные условия организованы по схеме «от события», «от момента времени».

Блок реализации повторных имитационных экспериментов обеспечивает переборочную процедуру по повторным реализациям.

С условием оговоренной особенности начальных условий нецелесообразно формировать неприкосновенную копию модельных начальных условий с последующим их тиражированием для каждой повторной реализации, и этот блок можно встраивать в блок реализации повторных имитационных экспериментов.

Блок обработки результатов повторных реализаций имитационного эксперимента подразумевает статистическую обработку значений оценок показателей состояния, оцененных для каждой повторной реализации для каждого дискретного момента их наблюдений.

Блок-имитатор объекта моделирования выполняет функции изменения состояния материальных квантов в дискретные моменты модельного времени.

В блоке-имитаторе объекта моделирования, в свою очередь, выделяются локальные блоки-имитаторы, задействованные для каждого очередного анализируемого материального кванта в зависимости от его нахождения в том или ином выделенном субподобъекте-доноре.

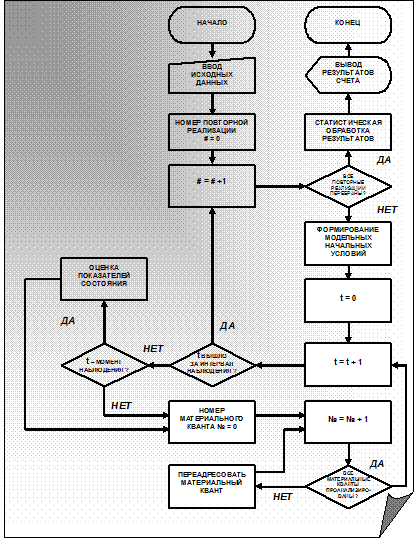
Общая схема функционирования имитационной модели на базе метода модельных переходов отражена на блок-схеме, представленной на рис. 2.5.

В содержательном плане функционирование осуществляется следующим образом.

Первоначально производится ввод исходных данных.

Далее организуется фиксированное число повторных итераций по повторным реализациям имитационного эксперимента.

Для каждой из этих итераций сначала производится формирование начальных модельных условий.

Затем организуется проведение каждой из предусмотренных повторных реализаций (их число задается априорно, исходя из требований по статистическим характеристикам подлежащих оцениванию показателей состояния).

С учетом низкого уровня стохастичности в модели число повторных реализаций имитационного эксперимента может быть ограничено десятью.

Для каждой из фиксированных повторных реализаций имитационного эксперимента организуются:

- оценка значений показателей состояния для фиксированной реализации и моментов времени, заданных как моменты оценки значений показателей состояния;

- переадресация материальных квантов из субподобъекта в субподобъект для каждого из выделенных дискретных моментов времени.

После завершения всех предусмотренных повторных реализаций имитационного эксперимента производится статистическая обработка его результатов по каждому из назначенных показателей состояния.

Рис. 2.5. Общая схема функционирования имитационной модели на базе метода переходов

Заканчивается процесс выводом результатов (оцененных показателей состояния) компьютерного прогнозного имитационного эксперимента.

И, наконец, завершим представление методов имитационного моделирования кратким рассмотрением гибридно-гибридного метода – метода параллельно-последовательных переходов.

За его основу принят уже рассмотренный выше метод переходов, но для моментов перехода построено последовательное диспетчеризуемое множество методов переходов и ключевых модельных событий – кортеж включений имитационных моделей на базе различных, в том числе гибридных методов, имитационного моделирования.

Метод параллельно-последовательных переходов состоит (см. рис. 2.6) в пошаговом продвижении по общемодельному времени с последовательным «послойным» воспроизведением динамики состояния объекта управления, трансформацией этих подсостояний в челночном, сканирующем или маятниковом режиме.

Рис. 2.6. Внутримоментная диспетчеризация переходов
(для случая двух подмоделей)

В том случае, если рассматривается только один слой, гибридно-гибридный метод превращается в обычный гибридный.

Необходимая точность при этом достигается за счет минимизации квантования шкалы модельного времени – теоретически она может быть сделана сколь угодно малой, но ограниченной, исходя из требований по реактивности управляющей системы и соответственно времени компьютерной имитации.

Таким образом, в общем случае методы имитационного моделирования предусматривают введение трехуровневой иерархической системы кортежей:

- временных кортежей по глобальному модельному времени;

- модельных кортежей для фиксированного момента глобального модельного времени;

- причинно-следственных, в том числе событийных, кортежей для фиксированной модели и фиксированного момента подмодельного времени.

В эту схему укладываются все известные методы имитационного моделирования, а также метод статистических испытаний (метод Монте-Карло), для которого все перечисленные кортежи являются одноэлементными – все они представлены универсальным одноэлементным кортежом, не имеющим привязки к физическому времени.

Date: 2015-05-23; view: 840; Нарушение авторских прав