Метод минимизирующих карт Карно

Этот метод по существу представляет собой тот же метод неопределенных коэффициентов, только записанный в более удобной форме.

Рассмотрим следующую таблицу

(3)

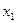
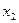
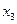
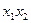
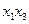
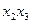
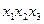
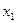
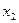
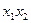
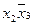
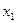
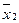
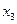
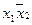
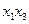
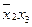
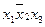
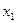
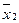
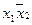
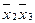
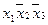
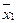
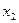
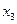
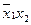
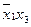
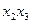
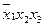
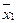
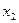
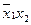
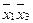
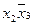
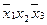
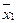
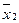
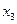
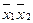
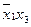
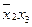
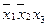
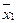
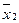
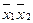
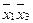
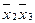
Эта таблица служит более компактной записью системы уравнений (1) метода неопределенных коэффициентов, где вместо коэффициентов 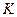в соответствующей клетке записываются сами конъюнкции. Каждая строка таблицы (3) заменяет собою соответственно 1-ое, 2-ое, …… 8-ое уравнения системы (1). Дизъюнкция всех элементов строки таблицы есть значение функции в вершине, определяемой соответствующими переменными. Так, первая строка есть значение функции в вершине 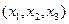, четвертая в 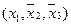или в переводе на координаты соответственно в (1, 1, 1), (1, 0, 0).

Можно показать, что если в СДНФ данной функции не входит какая-либо из восьми конъюнкций последнего столбца, то в минимальную форму этой функции не может входить ни одна из конъюнкций соответствующей строки таблицы.

Пусть, например, в СДНФ не входит конъюнкция 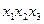, тогда в минимальную форму не входит, например, член 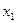(аналогично и другие конъюнкции 3-ей строки).

,

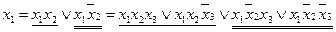Таким образом, если бы в минимальную форму входил член 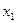, то обязательно входил бы член 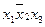, что противоречит предположению.

Таблица (3) и называется минимизирующей картой. Обычно эти карты отпечатаны для соответствующего числа переменных.

Минимизация функции производится по следующим правилам:

1. Все строки таблицы, которые соответствуют конъюнкциям последнего столбца, отсутствующим в СДНФ данной функции, вычеркивают.
2. В столбцах оставшихся строк вычеркивают все элементы, попавшие в вычеркнутые строки.
3. В каждой из невычеркнутых строк выбирают незачеркнутую конъюнкцию, содержащую минимальное число знаков (желательно, чтобы выбранные конъюнкции встречались чаще во всех оставшихся строках).
4. Взяв по одной конъюнкции для всех незачеркнутых строк и записав их дизъюнкцию, получают минимальную форму.

Заметим, что нахождение МДНФ неоднозначно, ибо произволен выбор минимальных конъюнкций в строках. Однако, все получаемые по этому методу МДНФ будут “одинаково минимальны”.

Пример 3. Минимизировать функцию (см. пример 1)

Строим для функции минимизирующую карту

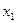
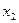
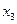
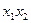
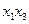
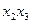
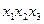
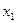
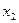
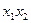
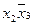
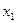
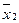
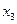
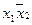
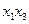
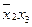
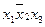
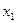
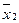
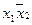
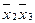
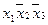
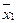
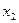
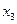
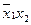
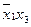
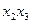
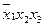
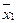
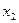
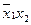
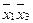
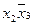
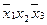
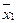
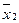
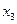
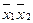
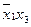
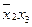
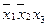
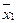
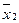
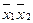
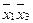
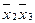
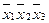
Отметим справа от последнего столбца те конъюнкции, которые входят в СДНФ данной функции. Вычеркнем неотмеченные строки (правило 1), затем вычеркнем в остальных строках (действуя по столбцу) те элементы, которые попали в вычеркнутые строки (правило 2). Во 2-ом столбце (с одной переменной) положим 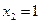, при этом остальные элементы строк (1, 2, 5, 6 строки), где стоит элемент 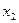, положим равными нулю. В строке 8 положим элемент , .

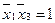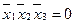Итак, получим МДНФ данной функции в виде:

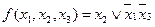
Сравните с результатами, полученными геометрическим методом и методом неопределенных коэффициентов.

Пример 4. Минимизировать функцию.

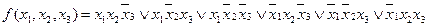
Согласно правилам 1, 2 вычеркиваем конъюнкции

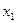
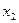
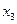
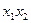
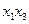
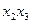
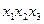
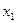
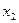
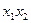
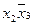
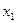
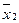
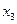
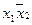
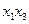
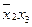
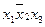
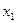
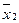
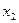
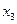
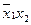
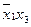
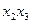
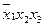
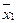
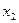
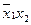
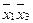
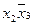
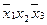
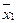
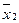
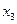
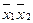
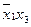
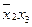
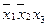
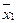
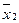
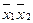
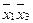
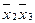
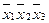
Для удобства табличку оставшихся конъюнкций начертим отдельно, выбросив 1-3 столбцы, 1, 8 строки.

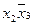
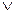
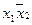
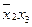
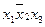
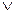
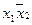
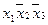
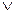
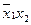
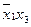
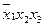
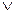
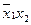
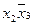
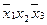
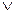
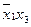
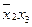
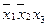
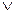
Положим во 2-ой строке 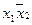равным 1, обведем рамочкой, остальные члены положим равными нулю. Вычеркнем нулевые члены 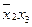в 6-й строке, в 1-й строке. Выберем из оставшихся строк самые короткие, 1-я и 6-я строки. Положим в них соответственно 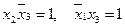, остальные члены равными нулю. В строках 4 и 5 будет по одному члену, равному 1. Итак, в каждой строке таблицы есть один член, равный 1, следовательно, минимальная форма функции будет

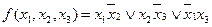
Возможен другой вариант минимальной формы. Рассмотрим на таблице.

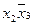
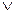
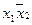
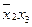
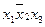
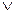
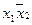
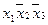
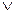
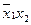
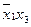
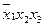
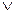
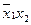
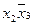
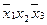
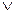
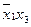
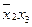
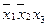
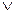
Пусть в 4-й строке 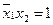, а остальные члены равны нулю. Тогда в строке 5: 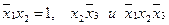можно положить равными нулю. Вычеркнем 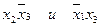в 1-й и 6-й строках (они короче других), положим соответственно 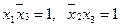. Тогда в строках 2 и 3 будет по одному члену, равному единице. Итак, минимальная форма функции

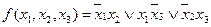
Методы неопределенных коэффициентов и минимизирующих карт приводят к громоздким записям (число строк таблицы для функции 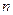переменных равно 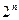, а число столбцов 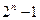). Использование этих методов уже для 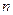порядка 8-10 становится затруднительным.

Date: 2015-05-22; view: 1112; Нарушение авторских прав