
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрический
|
|
Применяется он в основном для минимизации функций трех переменных, но его можно обобщить на любое количество переменных. Для трех метод нагляден. Поэтому ограничимся лишь этим случаем.
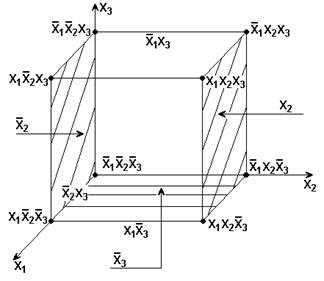 Изобразим область определения произвольной булевой функции трех переменных – это вершины трехмерного куба. Элементам куба можно поставить во взаимо-однозначное соответствие конъюнкции различного ранга: вершинам куба – конъюнкции третьего ранга, ребрам – второго, граням – первого. Каждый геометрический эквивалент меньшей размерности покрывается всеми геометрическими эквивалентами большей размерности. Конъюнкции большего ранга покрываются конъюнкциями меньшего ранга (см. рисунок).
Изобразим область определения произвольной булевой функции трех переменных – это вершины трехмерного куба. Элементам куба можно поставить во взаимо-однозначное соответствие конъюнкции различного ранга: вершинам куба – конъюнкции третьего ранга, ребрам – второго, граням – первого. Каждый геометрический эквивалент меньшей размерности покрывается всеми геометрическими эквивалентами большей размерности. Конъюнкции большего ранга покрываются конъюнкциями меньшего ранга (см. рисунок).
Так, например, конъюнкции 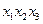 и
и 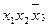 покрываются конъюнкцией
покрываются конъюнкцией 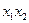 (две вершины – ребро);
(две вершины – ребро);
Конъюнкции 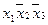 ,
, 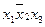 ,
, 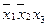 ,
, 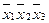 покрываются либо двумя конъюнкциями
покрываются либо двумя конъюнкциями 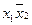 и
и 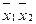 , либо только
, либо только 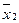 (четыре вершины – либо два ребра, либо одна грань).
(четыре вершины – либо два ребра, либо одна грань).
Булева функция задается множеством своих вершин, т.е. множеством единичных значений. Запись функции в некоторой ДНФ соответствует нахождению покрытия 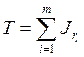 , где
, где 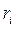 - ранги покрыва-ющих интервалов. Задача о нахождении минимальной ДНФ соответствует нахождению такого покрытия
- ранги покрыва-ющих интервалов. Задача о нахождении минимальной ДНФ соответствует нахождению такого покрытия 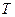 , в котором сумма рангов всех покрывающих интервалом является минимальной, т.е.
, в котором сумма рангов всех покрывающих интервалом является минимальной, т.е. 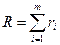 - минимально, ибо ранг
- минимально, ибо ранг 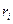 совпадает с числом букв, входящий в
совпадает с числом букв, входящий в 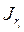 .
.
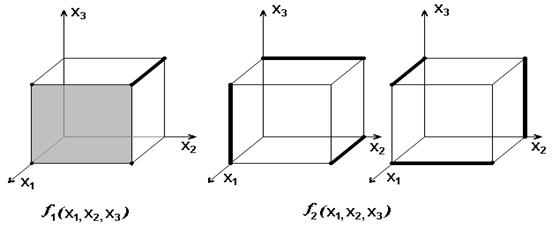
Для функций 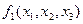 и
и 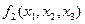 на приведенных ниже чертежах мини-мальными формами будут
на приведенных ниже чертежах мини-мальными формами будут 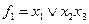 ,
, 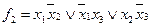 или
или 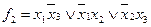 Для второй функции задача решается неоднозначно.
Для второй функции задача решается неоднозначно.
Пример: 1 Минимизировать функцию, заданную следующей таблицей истинности
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| f(x1, x2, x3) |
Ее формула в СДНФ имеет вид:
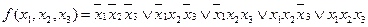
Отметим на чертеже вершины, соответствующие конъюнкциям, входящим в СДНФ данной функции.
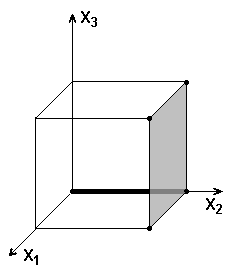 Заметим, что четыре вершины лежат в одной грани
Заметим, что четыре вершины лежат в одной грани 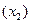 , а две на одном ребре
, а две на одном ребре 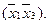 Откуда следует, что минимальная форма функции и есть сумма этих интервалов
Откуда следует, что минимальная форма функции и есть сумма этих интервалов 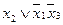 , т.е.
, т.е. 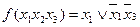 Другого варианта решения здесь не может быть. Задача решается однозначно.
Другого варианта решения здесь не может быть. Задача решается однозначно.
Date: 2015-05-22; view: 558; Нарушение авторских прав