Измерение ускорения свободного падения с помощью математического и физического маятников

Цель работы: измерение ускорения свободного падения с помощью математического и физического маятников.

Оборудование:

· штатив универсальный

· кронштейн с двумя гайками

· скоба

· математический маятник - шарик Æ 13 мм на нити

· оборотный маятник

· оптодатчик

· измерительный блок L-микро

· линейка

Периоды колебаний математического и физического маятников зависят от ускорения свободного падения g. Период колебаний T математического маятника равен:

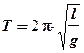, (1)

где l - длина нити математического маятника, точнее, расстояние от точки подвеса до центра шарика. В случае физического маятника

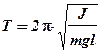, (2)

где m - масса физического маятника, l - расстояние от оси вращения до его центра масс, J ‑момент инерции физического маятника относительно оси вращения.

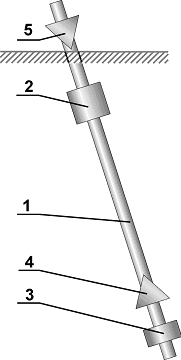Рисунок 1 Оборотный маятник 1- стержень,2,3-грузы, 4,5–оси вращения

Таким образом для определения g с помощью математического маятника достаточно измерить его период колебаний T и длину l, после чего рассчитать ускорение свободного падения g по формуле:

, (3

которая следует из (1).

Проводить измерения g с помощью произвольного физического маятника, опираясь на формулу (2), достаточно затруднительно, т. к. при этом необходимо знать точное значение его момента инерции, положение центра масс и массу. Однако существует прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции оборотного маятника.

Оборотный маятник является физическим маятником, который устроен следующим образом (см. рисунок1). На стержне (1) закрепляются два груза (2, 3). Стержень имеет две оси вращения (4, 5), расположенные, по разные стороны вращения по обе стороны от центра масс системы. Оси вращения для уменьшения трения выполняют в виде треугольных призм из твердого материала которые следует устанавливать на специальную опору (6), закрепленную на подставке.

оборотный маятник регулируется таким образом, чтобы период его колебаний при установке на одной призме равнялся периоду колебаний его на другой призме. Регулировка производится путем изменения взаимного расположения грузов и призм на стержне.

Выведем формулу периода колебаний оборотного маятника. Согласно теореме Штейнера момент инерции J маятника относительно произвольной оси вращения равен:

J=J_c+ml², (3)

где J_c - момент инерции относительно оси вращения, проходящей через центр масс, m - масса маятника, а l - расстояние от оси вращения до центра масс. После подстановки (3) в (2) формула для периода колебаний физического маятника примет вид:

. (4)

Поскольку оборотной маятника имеет равные периоды колебаний на обоих призмах (осях), на основании (4) можно записать:

,

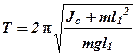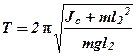. (5)

Здесь l₁ и l₂ - расстояния от центра масс маятника до ребра первой и второй призмы соответственно.

Возведем формулы (5) в квадрат и умножим на знаменатели правых частей:

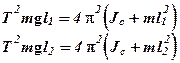
вычтем из первого равенства второе и сократим на m:

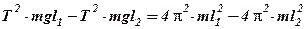
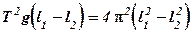
Применим формулу разности квадратов в правой части:

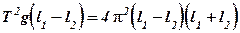(6)

Если в (6) l₁ ¹ l₂, что означает несимметричность расположения призм относительно центра масс маятника, то сокращая на (l₁-l₂), получаем:

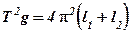(7)

Поскольку призмы расположены по разные стороны от центра масс, то l₁+l₂=l₀, где l₀ ‑расстояние между соответствующими ребрами призм (осями колебаний).

На основании (7) легко записываются выражение для периода колебаний оборотного маятника:

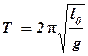, (8)

и формула для определения g:

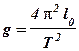(8)

Еще раз подчеркнем, что в случае l₁=l₂ (симметричное расположение осей колебаний относительно центра масс маятника), формулы (8) и (9) не являются справедливыми. Величина периода колебаний в этом случае зависит не только от l₀ и g, но и от момента инерции маятника.

В данной лабораторной работе с помощью оптодатчика измеряется промежуток времени между двумя ближайшими прохождениями груза маятника через положение равновесия, т.е. непосредственно измеряется половина периода колебаний