Основные формулы. 1. При равномерном прямолинейном движении линейная скорость:

1. При равномерном прямолинейном движении линейная скорость:

υ=s/t=const,

где s – перемещение, совершаемое за время t.

2. При равноускоренном прямолинейном движении справедливы соотношения:

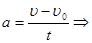
υ= υ₀+at,

s= υ₀t+ ,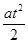

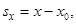
где υ₀ – начальная скорость; υ – скорость в момент времени t; s – перемещение, совершаемое за время t; a = const – линейное ускорение.

3. При криволинейном движении проекции ускорения на направления нормали и касательной к кривой в данной точке соответственно называют нормальным (центростремительным) 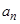и тангенциальным (касательным) :

.

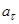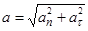4. Мгновенные центростремительное и тангенциальное ускорения при движении материальной точки по криволинейной траектории радиусом кривизны R:

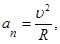
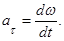
5. При равномерном вращении твёрдого тела вокруг оси угловая скорость:

ω = φ/t = const.

где φ – угол поворота радиуса, соединяющего центр окружности с движущейся точкой; t – время, за которое происходит этот поворот.

6. При равноускоренном вращении тела справедливы соотношения:

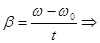ω = ω₀+βt,

j = ω₀t+ ,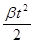

где ω₀ – начальная угловая скорость; ω – угловая скорость в момент времени t; φ – угловое перемещение, совершённое за это время; β = const – угловое ускорение.

7. В общем случае вращательного движения тела:

ω = dφ/dt и β = dω/dt = d²φ/dt².

8. Соотношения между угловой скоростью ω, периодом Т и частотой вращения v:

.

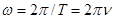9. Связь между линейными и угловыми кинематическими характеристиками:

s = φR, υ = ωR, a _t = βR.

10. Согласно второму закону Ньютона:

F = ma,

где m – масса тела, а – ускорение, приобретаемое им под действием силы F.

11. Закон изменения импульса (количества движения) за малый промежуток времени ∆t:

F∆t = mυ – mυ₀ ,

где ∆t – время действия силы F; υ₀,υ – начальная и конечная скорости движения тела соответственно.

12. Закон сохранения импульса (количества движения) в изолированной системе:

где m_i и υ_i – соответственно масса и вектор скорости i-го тела; 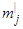и – соответственно масса и вектор скорости j-го тела.

13. Сила трения:

F_ТР= mN,

где m – коэффициент трения; N – сила нормального давления.

14. По закону всемирного тяготения сила взаимного притяжения двух материальных точек (или шарообразных тел), имеющих массы m₁ и m₂ и находящихся на расстоянии r друг от друга, выражается соотношением:

,

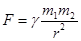где γ = 6,67·10^–11 Нм²/кг² – гравитационная постоянная (постоянная тяготения).

15. Работа постоянной силы F на перемещении s:

A = F·s·cosα,

где α – угол между направлениями силы и перемещения.

16. Для постоянной мощности имеют место выражения:

N = A/t = F·υ·cosα,

где А – работа, совершаемая за время t; F – сила; υ – скорость движения; α – угол между направлениями силы и скорости.

17. Кинетическая энергия тела массой m, движущегося поступательно со скоростью υ:

W_К= mυ²/2.

18. Потенциальная энергия упруго деформированного тела:

W_П= k∆x²/2,

где ∆x – величина деформации; k – коэффициент упругости.

19. Потенциальная энергия тяготения двух материальных точек (или шарообразных тел):

W_П= – ,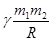

где m₁ и m₂ – массы тяготеющих тел; R – расстояние между ними; γ – гравитационная постоянная.

20. Потенциальная энергия тела массой m, приподнятого на небольшую высоту h над землёй:

W_П= mgh,

где g – ускорение свободного падения.

21. Момент силы F относительно некоторой оси вращения:

M = Fd,

где d – плечо силы, т.е. расстояние между осью вращения и прямой, вдоль которой действует сила.

22. Момент инерции материальной точки:

J = md²,

где m – масса материальной точки; d – расстояние от точки до оси вращения.

23. Моменты инерции (некоторых однородных тел геометрически правильной формы) относительно оси симметрии:

а) тонкого стержня J = 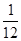mL², где l – длина стержня;

б) диска (цилиндра) J = 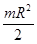, где R – радиус диска (цилиндра);

в) обруча (тонкостенного кольца) J =mR², где R – средний радиус обруча;

г) шара J = 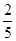mR², где R – радиус шара.

24. Условие равновесия твёрдого тела:

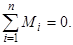
25. Основной закон динамики вращательного движения:

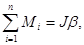
где М_i – момент i – той силы, J – момент инерции тела; β – угловое ускорение.

26. Теорема Штейнера:

,

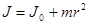где J ₀ – момент инерции тела относительно оси симметрии, J – момент инерции тела относительно произвольной оси, параллельной оси симметрии, r – расстояние между осями.

27. Закон сохранения импульса движения (момента импульса) в изолированной системе:

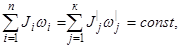
где J_i – момент инерции i -го тела; ω_i – вектор его угловой скорости, 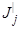– момент инерции j -го тела; 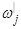– вектор его угловой скорости.

28. Кинетическая энергия вращающегося тела:

W_К = .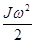

29. Для установившегося потока идеальной несжимаемой жидкости справедливы:

уравнение неразрывности струи:

υS = const

и уравнение Бернулли:

,

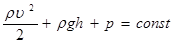где S – площадь поперечного сечения потока (трубки тока); υ и p – соответственно скорость течения и статическое давление жидкости; ρ – плотность жидкости; g – ускорение свободного падения.

Для горизонтальной трубки тока уравнение Бернулли имеет вид:

.

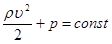30. Скорость вытекания жидкости из малого отверстия выражается соотношением (формула Торричелли):

,

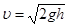где h – высота поверхности жидкости над отверстием.

31. Сила сопротивления, оказываемая жидкостью движущемуся в ней со скоростью υ шарообразному телу радиусом r, выражается законом Стокса:

F = 6πηrυ,

где η – коэффициент вязкости.

32. Объём жидкости, протекающей по трубе радиусом r за время t:

,

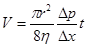где ∆p/∆x – градиент давления.

33. Уравнение гармонических колебаний:

x = Asin(ωt+φ₀),

где x – смещение колеблющейся величины от состояния равновесия в момент времени t; А – амплитуда; φ₀ – начальная фаза и ω – циклическая (круговая) частота колебаний.

34. Мгновенные скорость и ускорение точки, совершающей гармонические колебания:

;

.

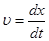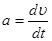35. Периоды гармонических колебаний:

а) математического маятника Т = 2π 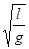, где l – длина подвеса,

б) груза на пружине T = 2π 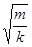, где k – жесткость пружины.

36. Кинетическая W_K, потенциальная W_П и полная W энергии гармонических колебаний:

W_K = ,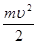

W_П = mgh или W_П = .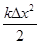

37. При сложении двух одинаково направленных гармонических колебаний (одинакового периода) получается гармоническое колебание (того же периода) с амплитудой:

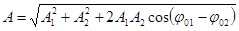
и с начальной фазой, определяемой из уравнения:

,

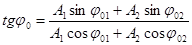где А₁ и А₂ – амплитуды слагаемых колебаний; φ₀₁ и φ₀₂ – начальные фазы колебаний.

38. При сложении двух взаимно перпендикулярных колебаний (одинакового периода) уравнение траектории результирующего движения имеет вид:

,

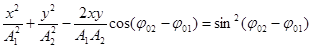где x и y – величины смещений в двух взаимно перпендикулярных колебаниях.

39. Длина волны λ, скорость υ её распространения и период Т связаны соотношением:

λ = υ Т.

40. Уравнение волны:

,

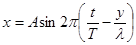где А – амплитуда; Т – период; λ – длина волны; х – смещение точки среды (участвующей в волновом процессе) в любой момент времени t; у – расстояние от этой частицы до источника волны.

41. Условие максимума и минимума интерференции двух когерентных волн:

max ∆ =2k 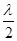= kλ, min ,

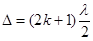где ∆ – оптическая разность хода волн (лучей); λ – длина волны; k = 0,1,2,….

42. Уравнение Клапейрона – Менделеева (уравнение состояния идеального газа):

pV = 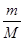RT,

где R = 8,314 Дж/(моль·К) – универсальная газовая постоянная; 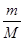= 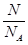– число молей, содержащихся в данной массе m газа; N – общее число частиц; N_A = 6,023·10²³ моль^-1 – число Авогадро; М – молярная масса; р – давление; V – объём; Т – температура газа по термодинамической шкале.

43. Давление р смеси различных газов равно (по закону Дальтона) сумме парциальных давлений p_i газов, составляющих смесь:

p = p₁+p₂+p₃+…+p_n= .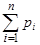

44. Основное уравнение молекулярно-кинетической теории газов:

,

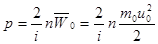где р – давление газа; 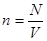– концентрация (число молекул в единице объёма); 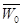– средняя кинетическая энергия поступательного движения одной молекулы; m₀ – масса молекулы; u₀ – средняя квадратичная скорость молекул, i – число степеней свободы молекул газа.

45. Число молекул в единице объёма газа:

,

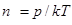где k=R/N_А = 1,38·10^–23 Дж/К – постоянная Больцмана; р и Т – соответственно давление и температура газа по термодинамической шкале.

46. Средняя квадратичная скорость молекул газа:

,

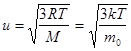где т₀ – масса молекулы.

47. Наиболее вероятная скорость молекул:

.

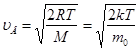48. Средняя арифметическая скорость молекул:

.

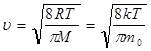49. Средняя кинетическая энергия (поступательного и вращательного движения) одной молекулы газа:

,

50. Внутренняя энергия газа (энергия теплового движения его молекул)

,

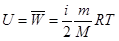где т – масса газа.

51. Связь между молярной c_m и удельной с теплоёмкостями:

c_m = Мс.

52. Молярная теплоёмкость при постоянном объёме:

c_mV = 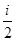R.

53. Молярная теплоёмкость при постоянном давлении:

c_mP = 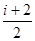R или c_mP = c_mV+R.

54. Отношение теплоёмкостей:

.

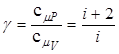55. Средняя длина свободного пробега молекул газа:

,

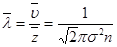где 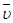– среднеарифметическая скорость молекул; 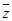– среднее число столкновений молекулы за секунду; 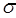– эффективный диаметр молекулы; n – концентрация молекул.

56. Масса газа ∆М, переносимая за время ∆t через площадку ∆S путём диффузии, определяется уравнением:

,

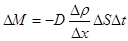где ∆ρ/∆x – градиент плотности; 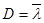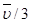– коэффициент диффузии.

57. Сила внутреннего трения:

,

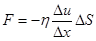где 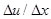– градиент скорости течения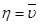 газа; – коэффициент внутреннего трения (вязкость); ρ – плотность газа; u – скорость течения газа.

58. Количество теплоты ∆Q, переносимое за время ∆t через площадку ∆S в результате теплопроводности, выражается соотношением:

,

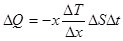где 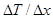– градиент температуры;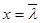 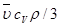– коэффициент теплопроводности; с_V – удельная теплоёмкость при постоянном объёме.

59. Осмотическое давление р раствора (закон Вант-Гоффа):

,

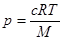где R – универсальная газовая постоянная; Т – температура раствора по термодинамической шкале; М – молярная масса растворённого вещества; c = m/V – концентрация раствора; т – масса растворённого вещества; V – объём раствора.

60. Коэффициент температуропроводности k связан с коэффициентом теплопроводности х, удельной теплоёмкостью с и плотностью ρ следующим соотношением:

k = x/cρ.

61. Коэффициент поверхностного натяжения жидкости:

α = F/l,

где F – сила поверхностного натяжения, действующая на контур длиной l.

62. Избыточное давление ∆р, вызванное кривизной поверхности жидкости, определяется формулой Лапласа:

,

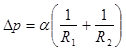где R₁ и R₂ – радиусы кривизны двух нормальных взаимно перпендикулярных сечений поверхности жидкости.

63. Высота поднятия (опускания) жидкости в капилляре определяется формулой Жюрена:

,

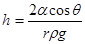где r – радиус капилляра; ρ – плотность жидкости; θ – краевой угол; g –ускорение свободного падения.

64. Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для любой массы т газа:

,

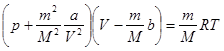где m – масса газа, V – объём; M – молярная масса; p – давление; T – температура газа по термодинамической шкале; a и b – константы (различные для разных газов), связанные с критическими значениями температуры T_k, давления p_k и объёма V_mk следующими соотношениями:

V_mk = 3b, p_k = a/27b², T_k = 8a/27bR.

65. Избыточное давление насыщенного пара над искривлённой поверхностью жидкости:

,

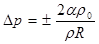где ρ – плотность жидкости; ρ₀ – плотность насыщенного пара; R – радиус кривизны поверхности; α – коэффициент поверхностного натяжения жидкости.

66. Относительное уменьшение давления насыщенного пара над раствором определяется законом Рауля:

,

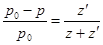где р₀ – давление насыщенного пара над чистым растворителем; р – давление насыщенного пара над раствором; 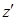– число молей растворённого вещества; z – число молей растворителя.

67. Первое начало термодинамики:

Q = ∆U + A^/,

где Q – количество теплоты, полученное системой; ∆U – изменение внутренней энергии системы; A^/ = p∆V – работа, совершаемая системой в изобарном процессе при изменении её объёма (р – давление, ∆V – изменение объёма системы). В общем случае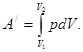

68. Работа, совершаемая при изотермическом изменении объёма газа:

,

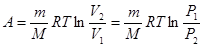где V₁ и V₂ – соответственно начальный и конечный объёмы газа, p₁ и p₂ - соответственно начальное и конечное давление газа.

69. Уравнения Пуассона для адиабатического процесса:

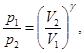
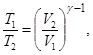
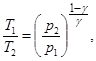
где р, Т и V - соответственно давление, температура по термодинамической шкале и объём газа, γ = с_P/с_V – отношение теплоёмкости газа при постоянном давлении к его теплоёмкости при постоянном объёме.

70. Работа, совершаемая при адиабатном изменении объёма газа:

.

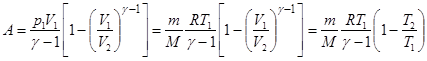71. Коэффициент полезного действия тепловой машины:

,

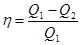где Q₁ – количество теплоты, переданное нагревателем рабочему телу; Q₂ – количество теплоты, отданное холодильнику.

72. Для цикла Карно:

,

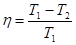Т₁ – температура нагревателя; Т₂ – температура холодильника.

73. Изменение энтропии системы при переходе из состояния А в состояние В:

,

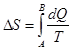где dQ – количество теплоты, переданное системе (или системой); Т – температура по термодинамической шкале, при которой происходила теплопередача.

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ

1. Предмет и задачи физики. Материя и её простейшие формы движения. Связь физики с другими науками и техникой. Задачи механики и молекулярной физики.

2. Система отсчёта. Путь, перемещение, скорость и ускорение. Прямолинейное равномерное и равноускоренное движение. Графики зависимости кинематических величин.

3. Движение точки по окружности. Угловые и линейные характеристики движения, связь между ними.

4. Нормальное, тангенциальное и полное ускорение. Криволинейное движение.

5. Свободное падение и движение тел, брошенных под углом к горизонту.

6. Первый закон Ньютона. Инерциальные и неинерциальные системы отсчёта. Принцип относительности Галилея.

7. Понятие о силе и массе. Второй закон Ньютона. Третий закон Ньютона. Границы применимости законов Ньютона.

8. Виды фундаментальных взаимодействий. Сложение сил. Упругие силы. Закон Гука. Силы трения. Международная система единиц СИ.

9. Импульс точки. Связь между силой и изменением импульса. Импульс системы материальных точек. Закон сохранения импульса. Принцип реактивного движения.

10. Работа и мощность. Работа силы трения, силы тяжести и упругих сил. Силы консервативные и неконсервативные.

11. Потенциальная, кинетическая и полная механическая энергия. Закон сохранения энергии в консервативных и неконсервативных системах.

12. Закон всемирного тяготения. Гравитационное поле, его напряжённость и потенциал. Сила тяжести и вес тела.

13. Понятие о невесомости. Космические скорости и движение искусственных спутников Земли.

14. Твёрдое тело как система материальных точек. Центр масс. движение центра масс.

15. Вращение твёрдого тела вокруг неподвижной оси. Угловая скорость и ускорение.

16. Кинетическая энергия вращающегося тела. Момент инерции тела. Момент силы.

17. Основное уравнение динамики вращательного движения тела. Элементы статики. Условия равновесия твёрдого тела.

18. Момент импульса. Закон сохранения момента импульса. Гироскоп, его применение в технике.

19. Гармонические колебания. Смещение, амплитуда, частота, период, фаза, скорость и ускорение колеблющейся точки.

20. Математический и пружинный маятники. Свободные и вынужденные колебания. Резонанс и его роль в технике. Затухающие колебания. Демпферы.

21. Идеальный газ. Законы Авогадро. Уравнение Менделеева-Клапейрона.

22. Изопроцессы. Абсолютная шкала температур.

23. Основное положение молекулярно-кинетической теории. Распределение скоростей молекул по Максвеллу и его опытное подтверждение.

24. Основное уравнение молекулярно-кинетической теории газов. Связь температуры с энергией движения молекул.

25. Длина свободного пробега молекул, число столкновений. Явления переноса (общая характеристика).

26. Явления переноса: диффузия.

27 Явления переноса: внутреннее трение.

28. Явления переноса: теплопроводность.

29 Коэффициенты переноса, их зависимость от давления. Барометрическая формула.

30. Первый закон термодинамики. Теплота и работа как формы передачи энергии. Работа при изопроцессах.

31. Теплоёмкость идеальных газов. Уравнение Майера. Понятие о квантовой теории теплоёмкостей.

32. Адиабатный процесс. Уравнение Пуассона. Работа при адиабатном процессе.

33. Цикл Карно и его КПД. Работа тепловых и холодильных машин.

34. Понятие об энтропии. Второй закон термодинамики и его статистический смысл. Критика идеи о “тепловой смерти Вселенной”.

35. Уравнение Ван-дер-Ваальса. Теоретические и экспериментальные изотермы реальных газов. Метастабильные состояния.

36. Критическое состояние. Сжижение газов и получение низких температур.

Date: 2015-05-22; view: 678; Нарушение авторских прав