
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Топологии структур
|
|

Структуры систем бывают разного типа, разной топологии (или же пространственной структуры). Рассмотрим основные топологии структур (систем). Соответствующие схемы приведены на рисунках ниже.
Линейные структуры:
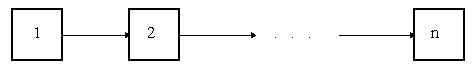
Рис. Структура линейного типа.
Часто понятие системы предполагает наличие иерархической структуры, т.е. систему иногда определяют как иерархическую целостность.
Иерархические, древовидные структуры:
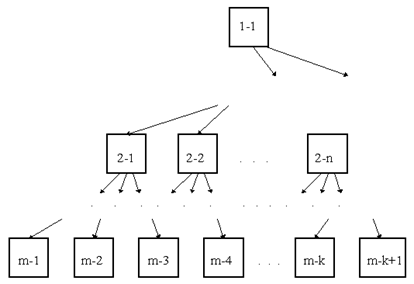 |
Рис. Структура иерархического (древовидного) типа.
Сетевая структура:
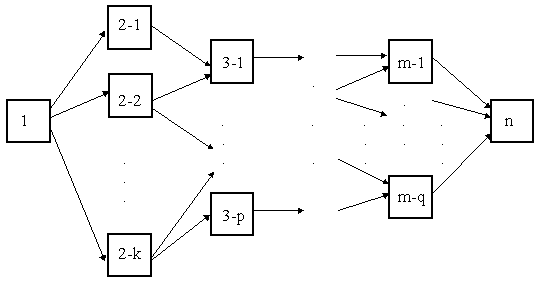
Рис. Структура сетевого типа.
 |
Матричная структура:
Рис. Структура матричного типа.
Пример. Примером линейной структуры является структура станций метро на одной (не кольцевой) линии. Примером иерархической структуры является структура управления вузом: “Ректор - Проректора - Деканы - Заведующие кафедрами и подразделениями - Преподаватели кафедр и сотрудники других подразделений”. Пример сетевой структуры - структура организации строительно-монтажных работ при строительстве дома: некоторые работы, например, монтаж стен, благоустройство территории и др. можно выполнять параллельно. Пример матричной структуры - структура работников отдела НИИ выполняющих работы по одной и той же теме.

Кроме указанных основных типов структур используются и другие, образующиеся с помощью их корректных комбинаций - соединений и вложений.
Пример. “Вложение друг в друга” плоскостных матричных структур может привести к более сложной структуре - структуре пространственной матричной (например, вещества кристаллической структуры типа изображённой на рис.). Структура сплава и окружающей среды (макроструктура) могут определять свойства и структуру сплава (микроструктуру):
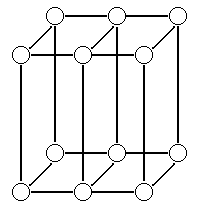 |
Рис. Структура типа кристаллической (пространственно-матричной).

Такого вида структуры часто используются в системах с тесно связанными и равноправными (“по вертикали” и “по горизонтали”) структурными связями. В частности, такую структуру могут иметь системы открытого акционерного типа, корпорации на рынке с дистрибьютерной сетью и другие.
Пример. Из комбинаций матрично-матричного типа (образуемую комбинацией “плоскостных”, например, временных матричных структур), можно получить, например, время - возрастную матричную “пространственную” структуру. Комбинация сетевых структур может дать вновь сетевую структуру. Комбинация иерархической и линейной структуры может привести как к иерархической (при “навешивании” древовидной структуры на древовидную), так и к неопределенностям (при “навешивании” древовидной структуры на линейную).

Из одинаковых элементов можно получать структуры различного типа.
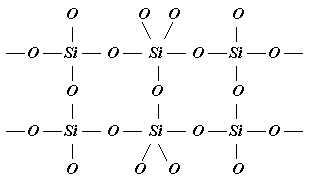 |
Пример. Макромолекулы различных силикатов можно получать из одних и тех же элементов (Si, O):
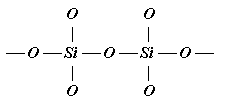
(а) (б)
Рис. Структуры макромолекул из кремния и кислорода (а, б).
Пример. Из одних и тех же составляющих рынка (ресурсы, товары, потребители, продавцы) можно образовывать рыночные структуры различного типа: ОАО, ООО, ЗАО и др. При этом структура объединения может определять свойства, характеристики системы.

Структура является связной, если возможен обмен ресурсами между любыми двумя подсистемами системы (предполагается, что если есть обмен i- ой подсистемы с j-ой подсистемой, то есть и обмен j-ой подсистемы с i-ой.

В общем случае, можно образовывать сложные, связные m-мерные структуры (m-структуры), у которых подсистемы - (m-1)-мерные структуры. Такие m-структуры могут актуализировать связи и свойства, которые невозможно актуализировать в (m-1)-структурах и эти структуры широко используются в прикладных науках (социология, экономика и др.) - для описания и актуализации сложных взаимосвязанных многопараметрических и многокритериальных проблем и систем, в частности, для построения указанных ниже когнитивных структурных схем (когнитивных карт).
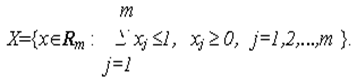

Указанного типа топологические структуры называют комплексами или симплициальными комплексами и математически их можно определить как объект K(X,Y,f), где X - это m-структура (mD-симплекс), Y - множество событий (вершин), f - связи между X и Y или математически:
Пример. Рассмотрим множество хороших друзей X={Иванов, Петров, Сидоров} и замечательных городов Y={Москва, Париж, Нальчик}. Тогда можно построить 3х мерную структуру в R3 (в пространстве трёх измерений - высота, ширина, длина), образуемую связыванием элементов X и Y, например, по принципу “кто где был” (рис.). В этой структуре использованы сетевые 2-х мерные структуры X, Y (в которых, в свою очередь использованы 1-структуры, например, расстояние между этими городами). При этом элементы X и Y можно брать как точки, рассматривая их как элементы пространства нулевого измерения - R0.

Рис. Геометрическая иллюстрация сложных связных структур.

Если структура плохо описываема или определяема, то такое множество объектов называется плохо структурируемым.
Пример. Плохо структурируемы будут проблемы описания многих исторических эпох, проблем микромира, общественных и экономических явлений, например, динамики курса валют на рынке, поведения толпы и др.

Плохо формализуемые и плохо структурируемые проблемы (системы) наиболее часто возникают на стыке различных наук, при исследовании синергетических процессов и систем.
Date: 2015-05-22; view: 2907; Нарушение авторских прав