
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчетные задания
|
|
Задача 1. Образует ли линейное пространство заданное множество, в котором определены сумма любых двух элементов 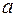 и
и 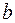 и произведение любого элемента
и произведение любого элемента 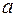 на любое число
на любое число 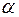 ?
?
1.1. Множество всех векторов трехмерного пространства, координаты которых – целые числа;
сумма  , произведение
, произведение 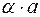 .
.
1.2. Множество всех векторов, лежащих на одной оси;
сумма  , произведение
, произведение 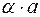 .
.
1.3. Множество всех векторов на плоскости, каждый из которых лежит на одной из осей;
сумма  , произведение
, произведение 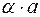 .
.
1.4. Множество всех векторов трехмерного пространства;
сумма  , произведение
, произведение 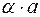 .
.
1.5. Множество всех векторов, лежащих на одной оси;
сумма  , произведение
, произведение 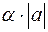 .
.
1.6. Множество всех векторов, являющихся линейными комбинациями векторов 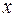 ,
, 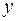 ,
, 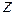 ;
;
сумма  , произведение
, произведение 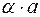 .
.
1.7. Множество всех функций 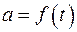 ,
, 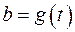 , принимающих положительные значения;
, принимающих положительные значения;
сумма 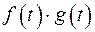 , произведение
, произведение 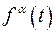 .
.
1.8. Множество всех непрерывных функций 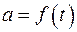 ,
, 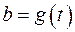 , заданных на
, заданных на 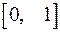 ;
;
сумма 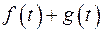 , произведение
, произведение 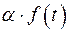 .
.
1.9. Множество всех четных функций 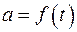 ,
, 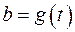 , заданных на
, заданных на 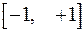 ;
;
сумма 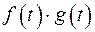 , произведение
, произведение 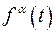 .
.
1.10. Множество всех нечетных функций 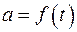 ,
, 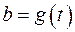 , заданных на
, заданных на 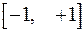 ;
;
сумма 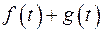 , произведение
, произведение 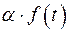 .
.
1.11. Множество всех линейных функций 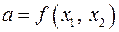 ,
, 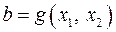 ;
;
сумма 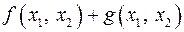 , произведение
, произведение 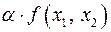 .
.
1.12. Множество всех многочленов третьей степени от переменной 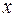 ;
;
сумма  , произведение
, произведение 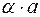 .
.
1.13. Множество всех многочленов степени, меньшей или равной трем от переменных 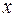 ,
, 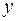 ;
;
сумма  , произведение
, произведение 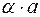 .
.
1.14. Множество всех упорядоченных наборов из 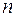 чисел
чисел
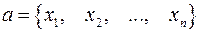 ,
, 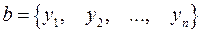 ;
;
сумма 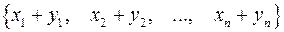 , произведение
, произведение 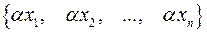 .
.
1.15. Множество всех упорядоченных наборов из 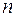 чисел
чисел
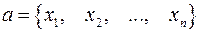 ,
, 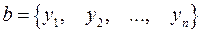 ;
;
сумма 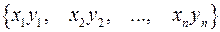 , произведение
, произведение 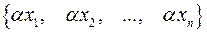 .
.
1.16. Множество всех сходящихся последовательностей 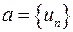 ,
, 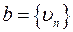 ;
;
сумма 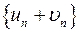 , произведение
, произведение 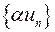 .
.
1.17. Множество всех многочленов от одной переменной степени меньшей или равной 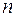 ;
;
сумма  , произведение
, произведение 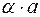 .
.
1.18. Множество всех многочленов от одной переменной степени 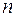 ;
;
сумма  , произведение
, произведение 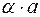 .
.
1.19. Множество всех диагональных матриц
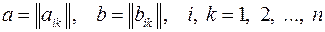 ;
;
сумма 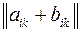 , произведение
, произведение 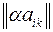 .
.
1.20. Множество всех невырожденных матриц
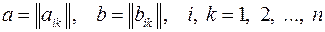 ;
;
сумма 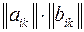 , произведение
, произведение 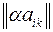 .
.
1.21. Множество всех квадратных матриц
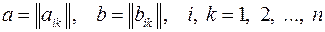 ;
;
сумма 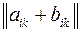 , произведение
, произведение 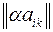 .
.
1.22. Множество всех диагональных матриц 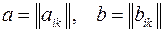 размера
размера 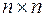 ;
;
сумма 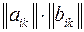 , произведение
, произведение 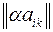 .
.
1.23. Множество всех квадратных матриц
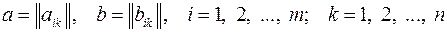 ;
;
сумма 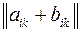 , произведение
, произведение 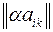 .
.
1.24. Множество всех симметричных матриц
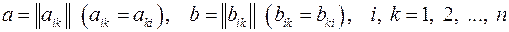 ;
;
сумма 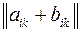 , произведение
, произведение 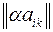 .
.
1.25. Множество всех целых чисел;
сумма  , произведение
, произведение 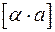 .
.
1.26. Множество всех действительных чисел;
сумма  , произведение
, произведение 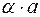 .
.
1.27. Множество всех положительных чисел;
сумма 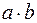 , произведение
, произведение 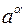 .
.
1.28. Множество всех отрицательных чисел;
сумма 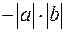 , произведение
, произведение 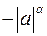 .
.
1.29. Множество всех действительных чисел;
сумма 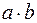 , произведение
, произведение 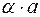 .
.
1.30. Множество всех дифференцируемых функций 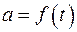 ,
, 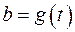 ;
;
сумма 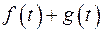 , произведение
, произведение 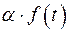 .
.
1.31. Множество всех дифференцируемых функций 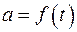 ,
, 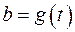 ;
;
сумма 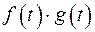 , произведение
, произведение 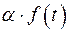 .
.
Задача 2. Исследовать на линейную зависимость систему векторов.
2.1. 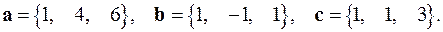
2.2. 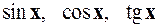 на
на 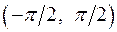 .
.
2.3. 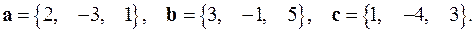
2.4. 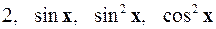 на
на 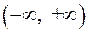 .
.
2.5. 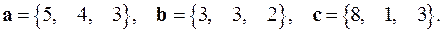
2.6. 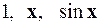 на
на 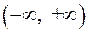 .
.
2.7. 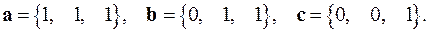
2.8. 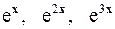 на
на 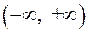 .
.
2.9. 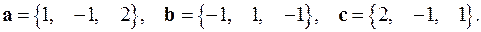
2.10. 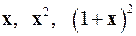 на
на 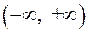 .
.
2.11. 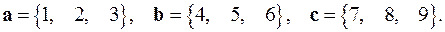
2.12. 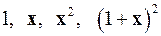 на
на 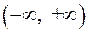 .
.
2.13. 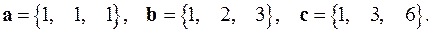
2.14. 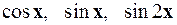 на
на 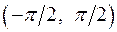 .
.
2.15. 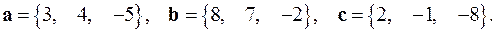
2.16. 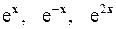 на
на 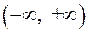 .
.
2.17. 
2.18. 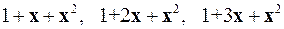 на
на 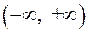 .
.
2.19. 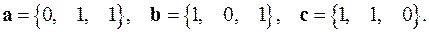
2.20. 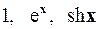 на
на 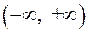 .
.
2.21. 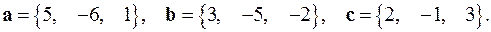
2.22. 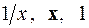 на
на 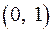 .
.
2.23. 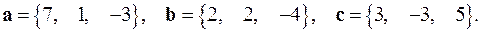
2.24. 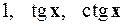 на
на 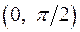 .
.
2.25. 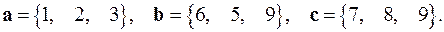
2.26. 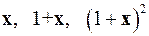 на
на 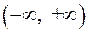 .
.
2.27. 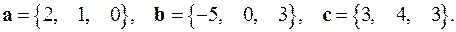
2.28.  на
на 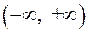 .
.
2.29. 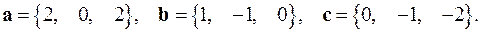
2.30. 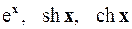 на
на 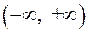 .
.
2.31. 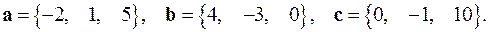
Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.
3.1. 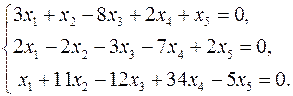 3.2.
3.2. 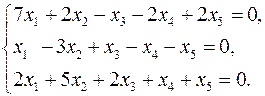
3.3. 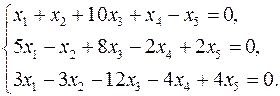 3.4.
3.4. 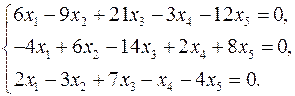
3.5. 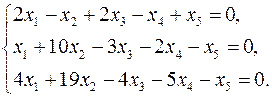 3.6.
3.6. 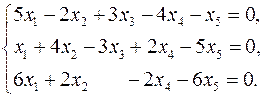
3.7. 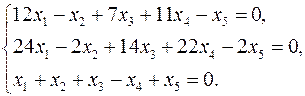 3.8.
3.8. 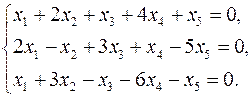
3.9. 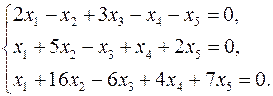 3.10.
3.10. 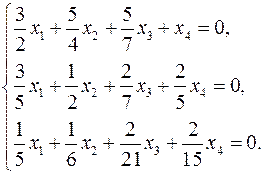
3.11. 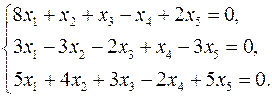 3.12.
3.12. 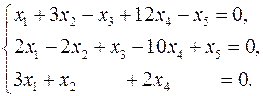
3.13. 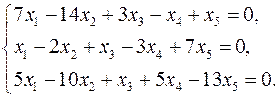 3.14.
3.14. 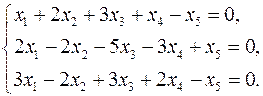
3.15. 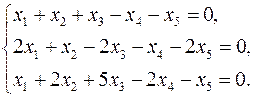 3.16.
3.16. 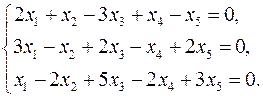
3.17. 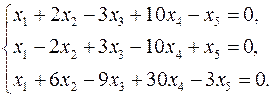 3.18.
3.18. 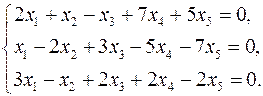
3.19. 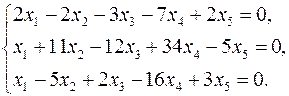 3.20.
3.20. 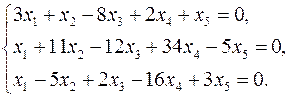
3.21. 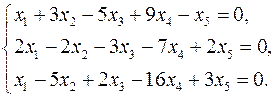 3.22.
3.22. 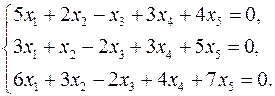
3.23. 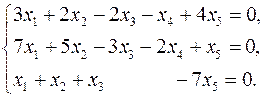 3.24.
3.24. 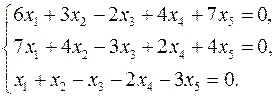
3.25. 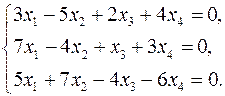 3.26.
3.26. 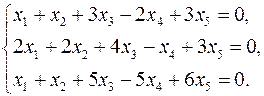
3.27. 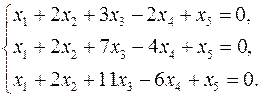 3.28.
3.28. 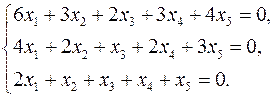
3.29. 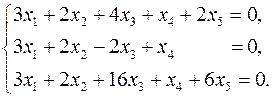 3.30.
3.30. 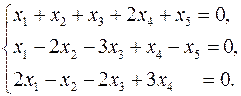
3.31. 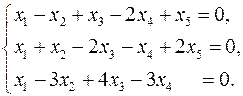
Задача 4. Найти координаты вектора 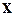 в базисе
в базисе 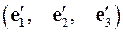 , если он задан в базисе
, если он задан в базисе 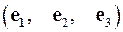 .
.
4.1. 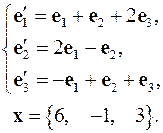 4.2.
4.2. 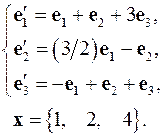
4.3. 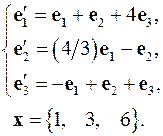 4.4.
4.4. 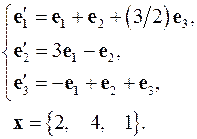
4.5. 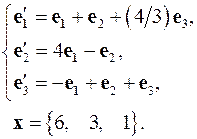 4.6.
4.6. 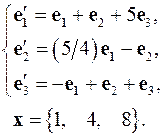
4.7. 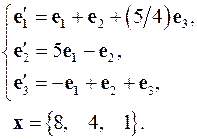 4.8.
4.8. 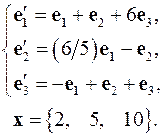
4.9. 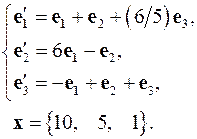 4.10.
4.10. 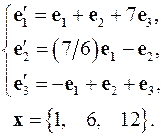
4.11. 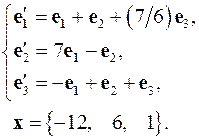 4.12.
4.12. 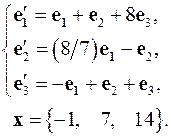
4.13. 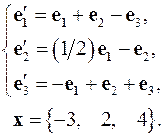 4.14.
4.14. 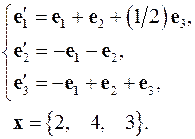
4.15. 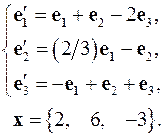 4.16.
4.16. 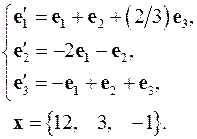
4.17. 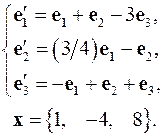 4.18.
4.18. 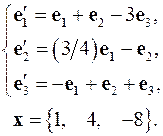
4.19. 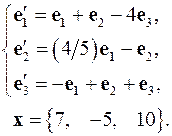 4.20.
4.20. 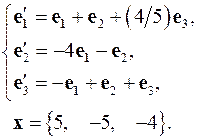
4.21. 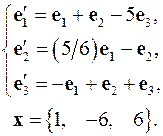 4.22.
4.22. 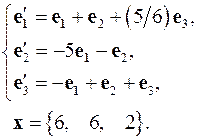
4.23. 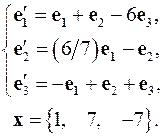 4.24.
4.24. 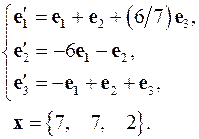
4.25. 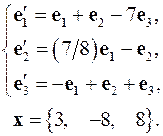 4.26.
4.26. 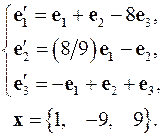
4.27. 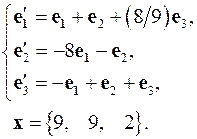 4.28.
4.28. 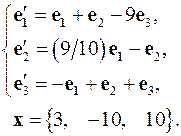
4.29. 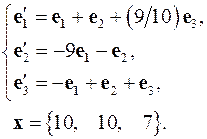 4.30.
4.30. 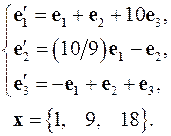
4.31. 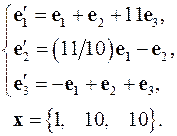
Задача 5. Пусть 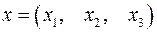 . Являются ли линейными следующие преобразования:
. Являются ли линейными следующие преобразования:
5.1. 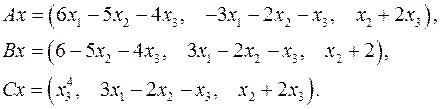
5.2. 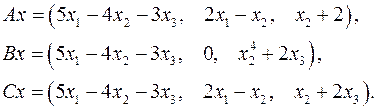
5.3. 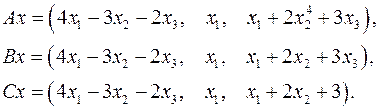
5.4. 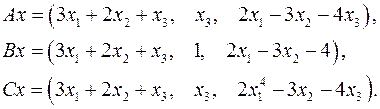
5.5. 
5.6. 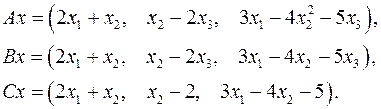
5.7. 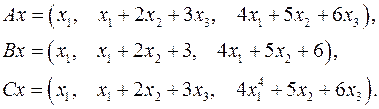
5.8. 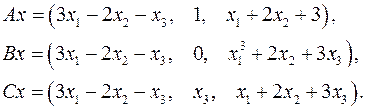
5.9. 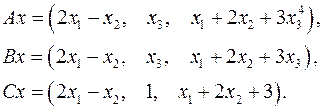
5.10. 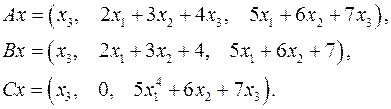
5.11. 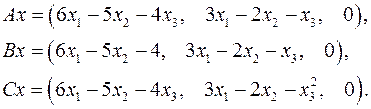
5.12. 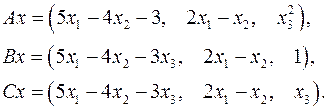
5.13. 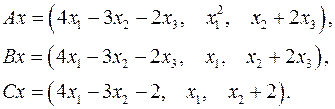
5.14. 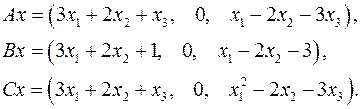
5.15. 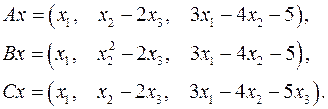
5.16. 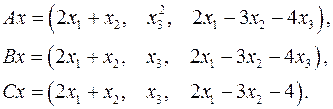
5.17. 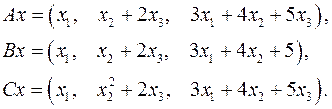
5.18. 
5.19. 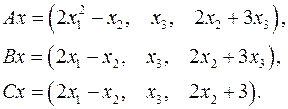
5.20. 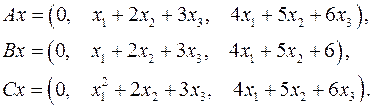
5.21. 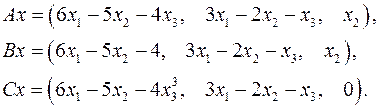
5.22. 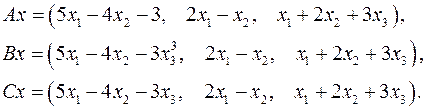
5.23. 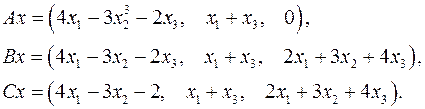
5.24. 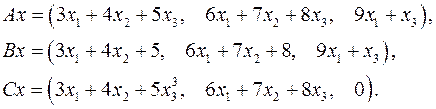
5.25. 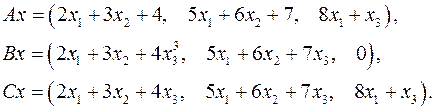
5.26. 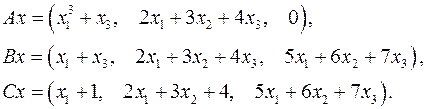
5.27. 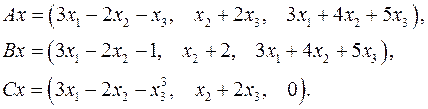
5.28. 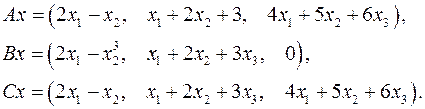
5.29. 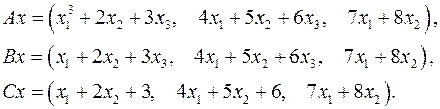
5.30. 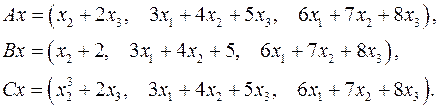
5.31. 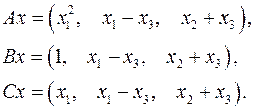
Задача 6. Пусть 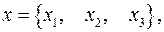
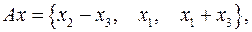
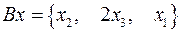 . Найти:
. Найти:
6.1. 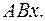 6.2.
6.2. 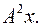 6.3.
6.3. 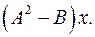
6.4. 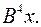 6.5.
6.5. 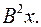 6.6.
6.6. 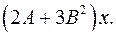
6.7. 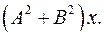 6.8.
6.8. 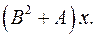 6.9.
6.9. 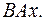
6.10. 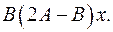 6.11.
6.11. 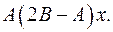 6.12.
6.12. 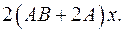
6.13. 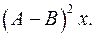 6.14.
6.14. 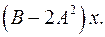 6.15.
6.15. 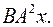
6.16. 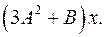 6.17.
6.17. 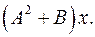 6.18.
6.18. 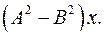
6.19. 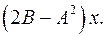 6.20.
6.20. 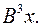 6.21.
6.21. 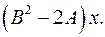
6.22. 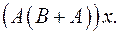 6.23.
6.23. 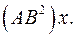 6.24.
6.24. 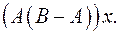
6.25. 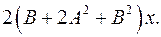 6.26.
6.26. 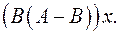 6.27.
6.27. 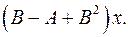
6.28. 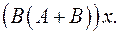 6.29.
6.29. 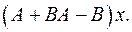 6.30.
6.30. 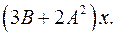
6.31. 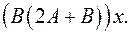
Задача 7. Найти матрицу в базисе 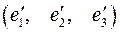 , где
, где
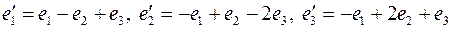 ,
,
если она задана в базисе 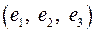 .
.
7.1. 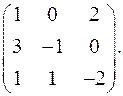 7.2.
7.2. 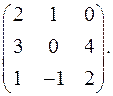 7.3.
7.3. 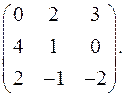
7.4. 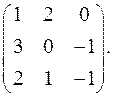 7.5.
7.5. 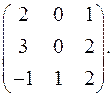 7.6.
7.6. 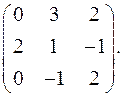
7.7. 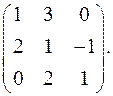 7.8.
7.8. 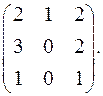 7.9.
7.9. 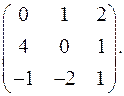
7.10. 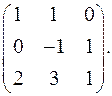 7.11.
7.11. 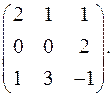 7.12.
7.12. 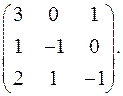
7.13. 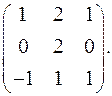 7.14.
7.14. 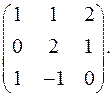 7.15.
7.15. 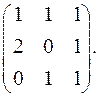
7.16. 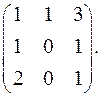 7.17.
7.17. 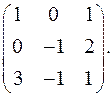 7.18.
7.18. 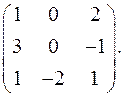
7.19. 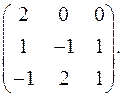 7.20.
7.20. 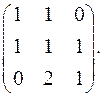 7.21.
7.21. 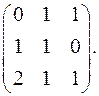
7.22. 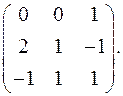 7.23.
7.23. 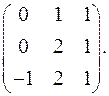 7.24.
7.24. 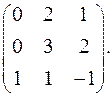
7.25. 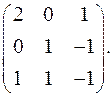 7.26.
7.26. 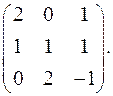 7.27.
7.27. 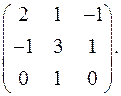
7.28. 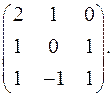 7.29.
7.29. 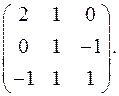 7.30.
7.30. 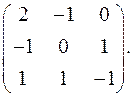
7.31. 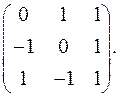
Задача 8. Доказать линейность, найти матрицу, область значений и ядро оператора:
8.1. проектирования на ось 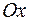 ;
;
8.2. проектирования на плоскость 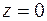 ;
;
8.3. проектирования на ось 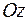 ;
;
8.4. зеркального отражения относительно плоскости 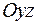 ;
;
8.5. проектирования на ось 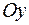 ;
;
8.6. проектирования на плоскость 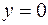 ;
;
8.7. зеркального отражения относительно плоскости 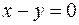 ;
;
8.8. зеркального отражения относительно плоскости 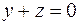 ;
;
8.9. проектирования на плоскость  ;
;
8.10. проектирования на плоскость 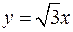 ;
;
8.11. проектирования на плоскость 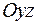 ;
;
8.12. зеркального отражения относительно плоскости 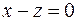 ;
;
8.13. зеркального отражения относительно плоскости 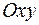 ;
;
8.14. поворота относительно оси 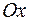 на угол
на угол 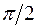 в положительном направлении;
в положительном направлении;
8.15. проектирования на плоскость 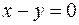 ;
;
8.16. проектирования на плоскость 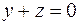 ;
;
8.17. зеркального отражения относительно плоскости 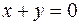 ;
;
8.18. зеркального отражения относительно плоскости  ;
;
8.19. проектирования на плоскость 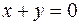 ;
;
8.20. проектирования на плоскость 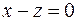 ;
;
8.21. зеркального отражения относительно плоскости 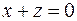 ;
;
8.22. поворота относительно оси 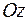 в положительном направлении на угол
в положительном направлении на угол 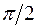 ;
;
8.23. проектирования на плоскость 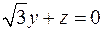 ;
;
8.24. зеркального отражения относительно плоскости 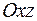 ;
;
8.25. поворота в положительном направлении относительно оси 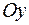 на угол
на угол 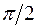 ;
;
8.26. проектирования на плоскость 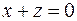 ;
;
8.27. проектирования на плоскость 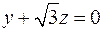 ;
;
8.28. проектирования на плоскость 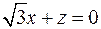 ;
;
8.29. проектирования на плоскость 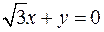 ;
;
8.30. поворота относительно оси 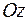 в положительном направлении на угол
в положительном направлении на угол 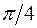 ;
;
8.31. проектирования на плоскость 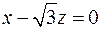 ;
;
Задача 9. Найти собственные значения и собственные векторы матрицы.
9.1. 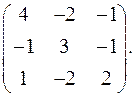 9.2.
9.2. 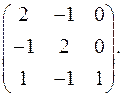 9.3.
9.3. 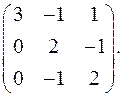
9.4. 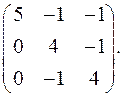 9.5.
9.5. 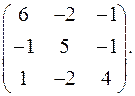 9.6.
9.6. 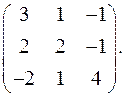
9.7. 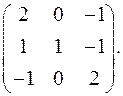 9.8.
9.8. 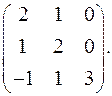 9.9.
9.9. 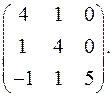
9.10. 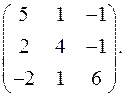 9.11.
9.11. 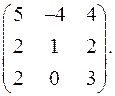 9.12.
9.12. 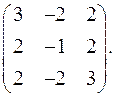
9.13. 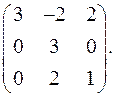 9.14.
9.14. 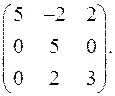 9.15.
9.15. 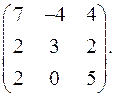
9.16. 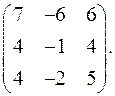 9.17.
9.17. 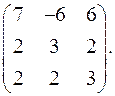 9.18.
9.18. 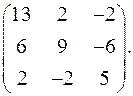
9.19. 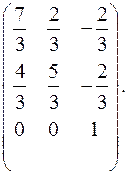 9.20.
9.20. 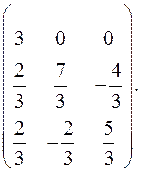 9.21.
9.21. 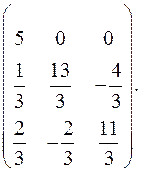
9.22. 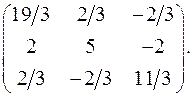 9.23
9.23 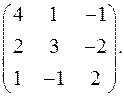 9.24.
9.24. 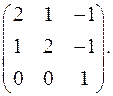
9.25. 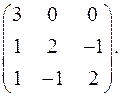 9.26.
9.26. 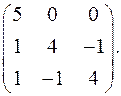 9.27.
9.27. 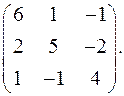
9.28. 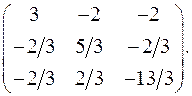 9.29.
9.29. 
9.30. 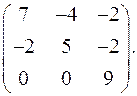 9.31.
9.31. 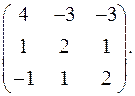
Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа.
10.1. 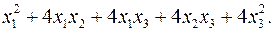
10.2. 
10.3. 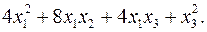
10.4. 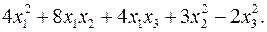
10.5. 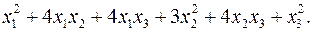
10.6. 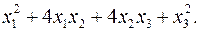
10.7. 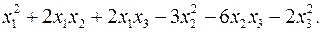
10.8. 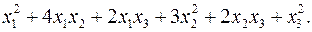
10.9. 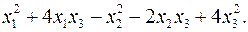
10.10. 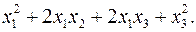
10.11. 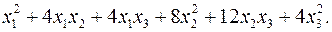
10.12. 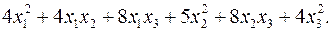
10.13. 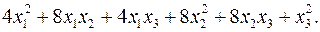
10.14. 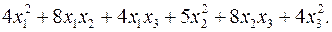
10.15. 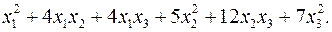
10.16. 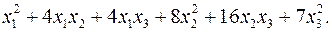
10.17. 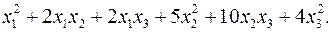
10.18. 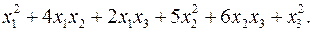
10.19. 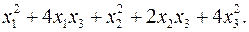
10.20. 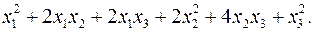
10.21. 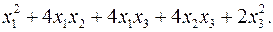
10.22. 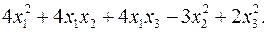
10.23. 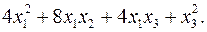
10.24. 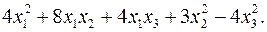
10.25. 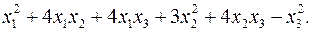
10.26. 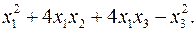
10.27. 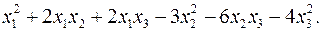
10.28. 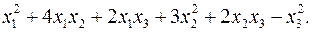
10.29. 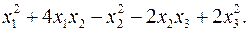
10.30. 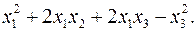
10.31. 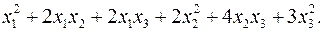
Задача 11. Привести квадратичную форму к каноническому виду ортогональным преобразованием.
11.1. 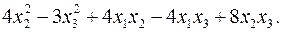
11.2. 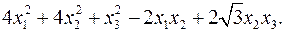
11.3. 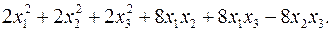
11.4. 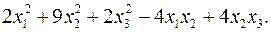
11.5. 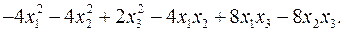
11.6. 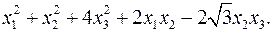
11.7. 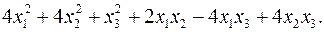
11.8. 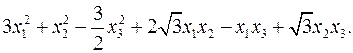
11.9. 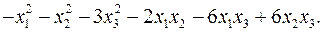
11.10. 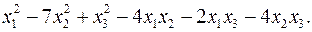
11.11. 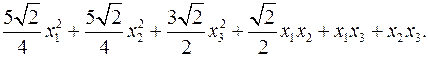
11.12. 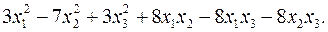
11.13. 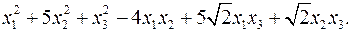
11.14. 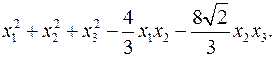
11.15. 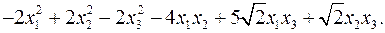
11.16. 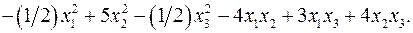
11.17. 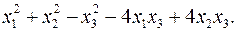
11.18. 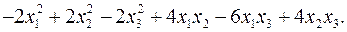
11.19. 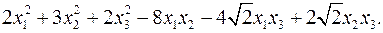
11.20. 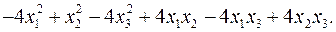
11.21. 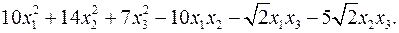
11.22. 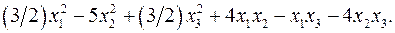
11.23. 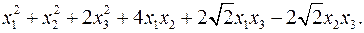
11.24. 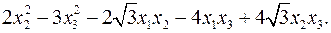
11.25. 
11.26. 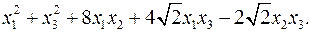
11.27. 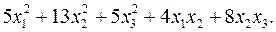
11.28. 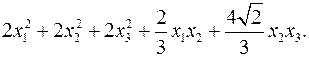
11.29. 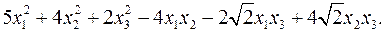
11.30. 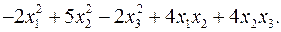
11.31. 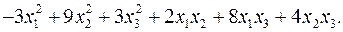
Задача 12. Исследовать кривую второго порядка и построить ее.
12.1. 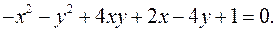
12.2. 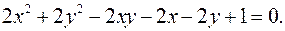
12.3. 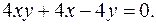
12.4. 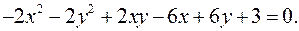
12.5. 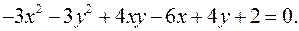
12.6. 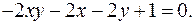
12.7. 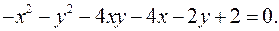
12.8. 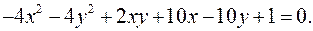
12.9. 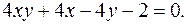
12.10. 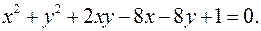
12.11. 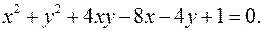
12.12. 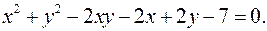
12.13. 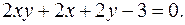
12.14. 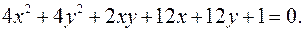
12.15. 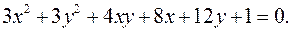
12.16. 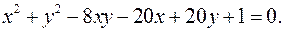
12.17. 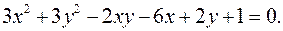
12.18. 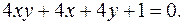
12.19. 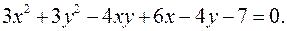
12.20. 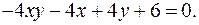
12.21. 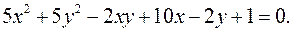
12.22. 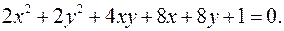
12.23. 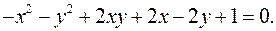
12.24. 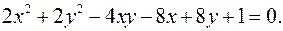
12.25. 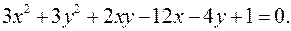
12.26. 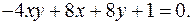
12.27. 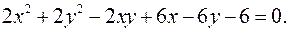
12.28. 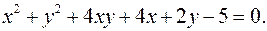
12.29. 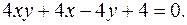
12.30. 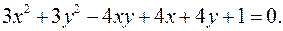
12.31. 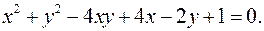
Date: 2015-04-23; view: 819; Нарушение авторских прав