Гармония золотых пропорций 12 page

И, наконец, Казанская церковь в Устюжне (рис. 5). Как и в предыдущих постройках, в ней два ордерных яруса. Высота I яруса − 640 см, II яруса − 713 см. В первом ярусе вновь та же сверхсажень 258 см, что в сольвычегодской церкви, и вновь в количестве 2½. Второй ярус оказывается равным 2½ саженям, повторенным дважды, т.е. можно считать его равным 5 ма­лым саженям по 142,4 см. Сдвоенные сажени к тому же могли носить и собственные наименования. Сажень близкого размера - 288 см, − указывает Г.Я. Романова, носила название «горо­довой» сажени. Поэтому второй ярус, возможно, представляет собой 2½ сажени городовых по 284,8 см.

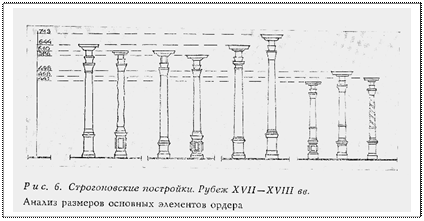
Таким образом, в белокаменном ордерном декоре (рис. 6) в строгановских постройках использована почти полная гамма древнерусских саженей в единой числовой структуре − 2½. Сооружения относятся к одному периоду, хотя и несколько рас­ходятся во времени постройки, к одной школе и сходны между собой по принципам пропорционирования; территориально они значительно разобщены.

Помимо перечисленных саженей и соподчиненных им единиц, существовали еще и другие величины, применявшиеся древнерус­скими зодчими в пропорционировании произведений архитектуры.

Сажень 217,6 см. Ряд башен Коломенского кремля − Возне­сенская, Ямская, Грановитая − указываются размером 17,4 м, что пересчитывается в старинные русские меры как 8 саженей по 217,6 см. Примерно таких же размеров оказывается сажень, показанная на линейном масштабе плана Москвы 1737 г. Это первая инструментальная съемка Москвы, выполнявшаяся главным архитектором города Мичуриным. Нами было произведено соразмерение линейного масштаба мичуринского чертежа с современным планом города. Брались характерные опорные объекты с различным взаимным удалением. Значение сажени колебалось в пределах 216 – 219 см.

Для близкой по значению сажени – 216 см – Б.А. Рыбаков указывает наименование «казенной». Мы применяем его для величины с нашим среднерасчетным значением 217,6 см (что, кстати, не превышает допускаемых отклонений).

Надо сказать, что казенная сажень употреблялась древнерус­скими зодчими в пропорционировании произведений архитектуры меньше других. В последующем казенная сажень была прирав­нена к английским 7 футам и обрела размер 213,36 см, ставший главенствующим в архитектуре XIX в.

В произведениях древнерусской архитектуры встречаются еще величины со среднерасчетными значениями - 134,5, 159,7 и др. Их названия (если только они были) пока не установлены. Ус­ловно мы именуем их «кладочными», так как они входят в состав размеров, хорошо согласующихся с габаритами кирпичной кладки в простенках и столбах.

Следует заметить, что, в отличие от современного кирпича, старинный, большеформатный (30 х 15 см) не был связан жестки­ми размерами с величиной простенков (для современного, напри­мер, требуются размеры 61-64-77-90-103-116-129 см и т.д.). Старинная кладка принимала любые размеры, так как шов не имел постоянной толщины. Но все же и для нее сущест­вовали как более, так и менее рациональные габариты простен­ков. Более подходящим был ряд следующих саженей, полусаже­ней и величин (в среднерасчетных значениях): 108,8 −115,2 − 122 − 134,5 −142,4 −150,8 −159,7.

Между величинами ряда разница около 7−8 см, примерно та­кая же, как между кирпичом полной длины (30 см) и его «трех­четверкой» − 3/4 частью кирпича (23 см), обрубавшейся для перевязки швов и обычно помещаемой по углам.

Мы невольно задаемся вопросом: в чем причина, и какие внутренние силы побуждали зодчих на протяжении многих веков пользоваться одними и теми же величинами, строить части и де­тали сооружений в одних и тех же размерах?

Иногда по поводу методики размерения зданий высказывается уже упоминавшееся нами мнение о якобы изображении на земле схемы абстрактных геометрических фигур, последующем перене­сении размеров с помощью циркульных дуг в каком-то закоди­рованном порядке в третье измерение и получении таким путем размеров на фасадах и разрезах архитектуры. Предшествующий рассмотренный нами материал не подтверждает таких предпо­ложений.

Какова должна быть циркульная засечка, чтобы высоту вось­мерика из с. Коломенского перенести в Новый Иерусалим?

Если функционируют постоянно употребимые величины, то не нужны дуги для их переноса.

Возникает иной вопрос: не в том дело, каким путем размеры попадали в третье измерение, по-видимому, не сложнее, чем в первое и второе, но почему столь устойчивыми они оказались в четвертом измерении − во времени? Какова причина длительного функционирования системы размеров? Если на протяжении мно­гих веков она способствовала созданию прекрасных произведений древнерусской архитектуры, то в чем конкретно состояла эффек­тивность ее воздействий?

Числовые системы пропорционирования

произведений архитектуры

Среди современных методов проектирования и пропорциони­рования зданий существует тенденция к применению определен­ных числовых систем, благодаря чему происходит упрощение процессов проектирования и достигаются большее единство и це­лостность решений. Вводятся различные «модули», стандартизи­руются сетки колонн (6 −12 − 24 − 36 м), производится упорядочение размеров балок, плит и т.д. Существуют специальные госты. В результате в структуре здания создаются четкие по­вторяющиеся ритмы, сокращается число типоразмеров элементов, упрощается строительство.

На протяжении многовековой истории древнерусской архи­тектуры мы встречаем однотипные габариты и размеры злемен­тов, деталей, помещений. Была ли и ранее какая-либо модульная или какая-то иная система, которая благоприятствовала опреде­ленным качествам древнерусской архитектуры? Существование единой стройной системы пропорционирования представляется не­вероятным, но вопрос этот не подвергался всестороннему рас­смотрению.

Б.А. Рыбаков систему древнерусских мер представил как еди­ную целостную систему с определенными закономерностями и ха­рактерными особенностями.

Связывая систему древнерусских мер с потребностями архи­тектуры, Б.А. Рыбаков показал геометрический характер взаимо­зависимостей некоторых мерных величин. В частности, в них сла­гались соотношения сторон и диагоналей квадратов. Графически мерные величины могли изображаться системой вписанных один в другой квадратов.

Такая система мер позволяла объяснить для культовых зда­ний домонгольского периода некоторые разбивочные операции, построение прямых углов, нахождение ряда размеров в наиболее сложной подкупольной части сооружения и по основным его осям. На примере Успенской церкви Елецкого монастыря в Чер­нигове была показана такого рода разбивка.

Однако сооружения последующих периодов − XV − XVI вв. и, особенно, XVII в.− с их развитыми многообразными формами, с целыми каскадами пышных белокаменных деталей, с виртуоз­ными, льющимися, подобно музыке, изгибами линий не могли, естественно, обслуживаться системой величин, привязанных к несложной схеме нескольких квадратов. Системам пропорциони­рования вообще свойственно отражение более общих закономер­ностей, и они не объясняются какой-либо схемой здания, тем более упрощенной.

В этот период, по-видимому, в мерах возникли новые или не­сколько изменились некоторые прежние отношения.

Различные системы, предназначенные для пропорционирова­ния и ускорения архитектурного проектирования, создаются вплоть до настоящего времени; не было препятствий к их функционированию и в прошлом; некоторые из современных находят себе преемственные прообразы в прошлых, несмотря на карди­нальные изменения, произошедшие в современной архитектуре. Укажем, например, на разработки выдающегося французского ар­хитектора Корбюзье. Его система пропорционирования, так на­зываемый «модулор» (в которой, кстати, также делаются попытки увязки с системой мер), при относительно небольшом составе ве­личин способствует достижению в архитектуре эстетически со­вершенных пропорций, обеспечивает многовариантность компо­новок и соразмерение получаемых габаритов с человеком. Вели­чины системы разработаны на основе модели человека. Система Корбюзье обобщила некоторый опыт современной и прошлой за­падноевропейской архитектуры и архитектурной математики.

Однако следует начать с работы знаменитого итальянского математика Леонардо Пизанского (Фибоначчи). В XIII в. он опубликовал числовой ряд, вошедший впоследствии в различ­ные системы пропорционирования.

Этот числовой ряд называется его именем и имеет следую­щий вид:

1−2−3−5−8−13−21−34−55−89−144−233−377 …

Каждый последующий член ряда равен сумме двух предыдущих:

1+2 = 3, 3 + 5 = 8, 8 +13 = 21...

А отношение двух соседних приближается к величине золотого сечения (Ф = 1,618...) особенно по мере увеличения порядковых номеров членов ряда:

5:3 = 1,666; 13: 8 = 1,625; 34: 21 = 1,619; 144: 89 = 1,618...

Золотое сечение известно в архитектуре и изобразительном искусстве с античных времен (возможно, употреблялось и ранее). Наименование «золотое» принадлежит Леонардо да Винчи. Пропорции и отношения, построенные на золотом сечении, обла­дают исключительно высокими эстетическими качествами. Оно свойственно объектам живой природы − растениям, раковинам, различным живым организмам, включая самого человека.

Золотое сечение (его условное обозначение Ф) устанавливает наивысшую соразмерность между целым и частями. Возьмем от­резок и разделим его так, чтобы весь отрезок (а + b) относился к большей части (а), как большая часть (а) − к меньшей (b), т. е.

(a+b) ∕ а = а ∕ b.

Тогда найденное после решения квадратного уравнения отно­шение a ∕ b будет равно величине золотого сечения, выражаемого бесконечной дробью: а/b = Ф = 1,618034...

Соразмерность частей и целого − необходимое условие любого произведения искусства. Лучшие произведения архитектуры всех времен и народов всегда строились соразмерными во всех своих частях, использовали золотое сечение и производные от него функции.

Последовательное деление в золотом отношении может быть продолжено, можно получить ряд величин, подобно ряду чисел Фибоначчи, но, в отличие от него, помимо возрастания, еще и в убывающую сторону.

В восходящую сторону:

1 −1,618... −2,618... −4,236... − 6,854... −11,090...

В нисходящую сторону:

1 −0,618... −0,382... −0,236... − 0,146... −0,090...

Эти ряды называются золотыми геометрическими прогрессия­ми. Знаменателем прогрессии является величина золотого сечения (знаменателем называется число, на которое умножается предыдущий член для получения последующего). В возрастающей про­грессии − знаменатель 1,618...; в убывающей −1∕ 1,618 = 0,618…

3олотые прогрессии - единственные из всех геометрических прогрессий, где последующий член ряда может получаться так же, как и в ряду Фибоначчи, еще и сложением двух предыдущих членов (или вычитанием для убывающей). В отличие от чисел ряда Фибоначчи члены золотой геометрической прогрессии − бесконечные дроби (иногда исключением, как в данном случае, может быть лишь исходный =1).

Итак, несоизмеримые отрезки золотого сечения устанавливают наивысшую соразмерность частей и целого. В ряду Фибоначчи они возникают по мере удаления, когда отношения все более приближаются к золотому сечению.

Характерно и еще одно свойство, общее для рядов Фибоначчи и золотого сечения. Числам этих рядов свойственна многовариантная слагаемость с получением результирующего в их же си­стеме:

3 + 5 = 8,

3 + 5 +13 = 21,

3 + 5 +13 + 34 = 55,

3 + 5 + 5 = 13; 3 + 5 + 5 + 8 = 21 и т. д.

Следует обратить особое внимание на эти комбинаторные свойства чисел ряда. Понимая под комбинаторной ветвь матема­тики, исследующую комбинации и перестановки предметов, мы хотели бы подчеркнуть, что именно благодаря указанной взаимной соразмерности и сопоставимости величин ряда Фибоначчи обеспечивается возможность получения многообразных компоно­вок. Если размеры некоторого ограниченного количества элемен­тов принять в величинах ряда Фибоначчи, то становится воз­можным образование из них более крупных габаритов и форм, взаимно соразмеренных и композиционно совместимых как меж­ду собой, так и в своих частях. Величины ряда Фибоначчи спо­собствуют получению весьма интересных и многовариантных компоновочных решений.

Видимо, поэтому живая природа в своих построениях и ком­поновках часто прибегает к отношениям золотого сечения и вели­чинам этих рядов.

Модулор Корбюзье как математическая система построен на двух рядах Фибоначчи (Корбюзье условно назвал их «линия­ми» − красной и голубой), взаимно соотносящихся между собой путем удвоения. Продолжая начатый пример, покажем схему комбинаторики модулора Корбюзье. Добавим еще ряд удвоенных величин с сохранением условных наименований рядов:

красная линия: 3−5−8−13−21−34−55...;

голубая линия: 4−6−10­−16−26−42−68...

В каждом из рядов существует слагаемость величин, о кото­рой говорилось выше, но, помимо нее, происходит еще и совмест­ная слагаемость величин обоих рядов. Многочисленные вариан­ты сложения можно разбить, например, на такие группы:

1) красные величины в сумме дают голубую: 3 + 5 + 13 + 21 = 42,

2) красные и голубые в сумме дают красную: 3 + 10 + 42 = 55,

3) красные и голубые в сумме дают голубую: 3 + 5 + 8 + 26 = 42,

4) красные и голубые, взятые по несколько раз, в сумме дают голубую:

2 х 5 + 2 х 16 = 42,

5) то же, но красную: 1 х 4 + 2 х 6 + 3 х 13 = 55 и т.д.

Этим далеко не исчерпываются возможные варианты. Коли­чество величин в системе хотя и удвоилось, но комбинаторика возросла многократно как в абсолютном значении, так и в отно­сительном (в расчете количества вариантов на 1 величину).

Небольшое количество величин позволило получать весьма много разнообразных компоновок.

Построив с использованием модулора всемирно известный дом в Марселе, Корбюзье писал: «Я дал задание проектировщикам мастерской составить номенклатуру всех использованных в здании размерных величин. Оказалось, что пятнадцати размерных величин было вполне достаточно. Всего пятнадцать!». Это весьма и весьма показательно. Правда, в названном количестве не учтены, видимо, суммарные, дробные и другие виды размеров; а лишь модулорные, но и они дают представление о высоких воз­можностях комбинирования с помощью системы «модулор».

Все величины модулора были увязаны с моделью человека. За исходные параметры модели Корбюзье принял рост, равный 6 футов = 183 cм, и размер в положении с поднятой рукой = 226 см. От исходных величин по математическим закономерностям чисел Фибоначчи Корбюзье вычислил все остальные и получил в сан­тиметрах:

красная линия: 16−27−43−70−113−183...

голубая линия: 20−33−53−86−140−226...

На рисунках, выполненных Корбюзье, показывалось, как эти ве­личины согласуются с размерами и положениями тела человека. 3а создание системы «модулор» Корбюзье получил патент и всемирное признание.

Укажем на некоторые распространенные виды пропорций, ко­торые строятся величинами модулора:

Ф = 1,618... 2/ Ф = 1,236... Ф ²/2 = 1,309... 2/ Ф ² = 0,472...

Последнее отношение представляет собой одну из так называе­мых «функций Жолтовского».

И.В. Жолтовскому, выдающемуся зодчему современности, назначенному еще в первые годы Советской власти при В.И. Ленине главным архитектором Москвы, принадлежит научное обоснование и практическое внедрение в современную прак­тику эстетически наиболее ценных и изысканных пропорций в архитектуре, производных от золотого сечения. Он выявил их, исследуя лучшие произведения античности и ренессанса, точно рассчитал и применял в современной архитектуре. В частности, И.В. Жолтовский при анализе пропорции Парфенона в отноше­ниях между диаметром колонны и интерколумнием, между высо­той антаблемента и фронтона указывает отношение, составляю­щее в числовом выражении 528: 472. Чтобы получить малый отрезок, характеризующий это отношение, Жолтовский в убы­вающем ряде золотой геометрической прогрессии берет значение третьего порядка − 0,236, удваивает его и получает 0,472. Вы­читание этой величины из единицы дает 0,528. Отношение 528: 472 было названо «функцией Жолтовского».

Учитывая, что в древнерусской архитектуре встречается очень много отношений, как по функции Жолтовского, так и по отдель­ным ее составляющим, мы ввели в целях удобства изложения материала, следующие условные наименования, которыми ниже 6yдем пользоваться:

0,472 − первая составляющая функции Жолтовского, или со­кращенно − первая функция Жолтовского с условным обозначением Fж₁

0,528 − вторая составляющая функции Жолтовского, или со­кращенно − вторая функция Жолтовского с условным обозначением Fж₂.

0,528: 0,472 = 1,118...− основная функция Жолтовского, или функция Жолтовского с условным обозначением Fж.

Корбюзье успешно использовал функции Жолтовского в своем марсельском доме. Перед началом строительства дома был зало­жен символический камень шириной 86 см и длиной 183 см. «Этот крупный камень, − писал Корбюзье, − действительно, об­ладает изяществом, и он послужил для прославления модуло­ра...».

В соотношении размеров камня 86: 183 = 0,472... мы узнаем первую функцию Жолтовского, благодаря чему и возникло изя­щество, о котором упомянул Корбюзье.

Размеры камня (86 и 183 см) брались по величинам модуло­ра. Но в модулоре строились не все функции Жолтовского; полу­чалась главным образом лишь первая (0,472); вторая − воспроизводилась сложным путем, и практически не возникала и основ­ная функция. To же самое относится и к ряду других ценных в архитектурном отношении пропорций.

Таким образом, обладая в качестве системы пропорциониро­вания многими полезными качествами, модулор все же не создал возможностей для построения полной гаммы лучших архитектур­ных пропорций.

Упомянем еще об одном весьма существенном недостатке мо­дулора, пожалуй, принципиальном его недостатке. В своей основе система величин имеет одну модель человека. Только одного человека. Сразу же при разработке величин возникал вопрос, како­го человека взять за образец, и, по-видимому, как само собой ра­зумеющееся брался средний или выше среднего человек. В пер­вом варианте модулора он был ростом 175см, а в положении с поднятой рукой имел размер 216 см. От этих исходных величин и были подсчитаны все остальные.

Обычно средний человек мыслится более характерным и эта­лонным. Ho последующие исследования в специальных областях, связанных с проектированием оборудования и помещений со стро­го регламентированными условиями пребывания в них людей, по­казали, что подобные положения являются неправильными.

«Создание машины в расчете на „среднего человека" является серьезной ошибкой. Если машина спроектирована на основании данных величин, соответствующих 50-му перцинтилю любой груп­пы людей (т. е. средним значениям − А.П.), то ею смогут нор­мально управлять только 50%людей из этой группы. Например, 50% операторов более низкого роста будут не в состоянии дотя­нуться до органов управления. Следующая ошибка концепции „среднего человека" в том, что она игнорирует вариативность людей. Только у небольшого количества людей размеры могут быть средними во всех отношениях...». Далее в упомянутом труде следует вывод о необходимости проектирования не на сред­него человека, а на определенный размерностный диапазон людей и дается методика такого проектирования. Действительно, женщины, например, всегда меньше ростом и, если все делать по высокому или среднему человеку, для них многое в интерьере жилого помещения, на кухне и т.д. окажется недосягаемым и неудобным.

По-видимому, Корбюзье именно в этом ощущал недостатки своей системы, когда неоднократно менял модели людей. 3а первым следовал второй вариант модулора, с моделью человека ростом 183 см и размером в положении с поднятой рукой − 226 см Были и еще варианты. Все они существовали независимо один от другого, но целостной системы, в которой присутствовал бы необходимый диапазон моделей людей, у него не получилось.

Древнерусский «всемер»

Рассмотрим более развитый вариант системы величин пропор­ционирования, дополнив двухрядную модулорную схему новыми рядами Фибоначчи:

24 40

12 20 32 52

6 10 16 26 42

3 5 8 13 21 34 55

1,5 2,5 4 6,5 10,5 17 27,5 44,5

0,75 1,25 2 3,25 5,25 8,5 13,75 22,25 36 58,25 и т.д. Все горизонтальные линии являются здесь, рядами Фибоначчи (в средней части − третий и четвертый снизу − знакомые нам ряды схемы модулора). Во вновь дополненных рядах, так же как и в прежних, сумма двух предыдущих членов равна последующе­му, а отношение двух соседних приближается к величине золотого сечения (тем больше, чем дальше от начала ряда). По верти­кальным направлениям мы продолжили структуру удвоения ве­личин (вверх) и половинных значений (вниз); поэтому отноше­ние по вертикали составляют 1: 2: 4: 8....