Метод обратных лучей

Метод обратных лучей успешно применяется при построении теней, падающих от одной геометрической фигуры на другую, и характеризуется следующими построениями:

а) строятся тени, падающие от обеих заданных фигур на какую-либо плоскость;

б) выявляются точки пересечения теней от двух линий, из которых одна принадлежит контуру первой фигуры, а другая — контуру второй;

в) при помощи обратных лучей (то есть лучей, параллельных лучам света, но имеющих обратное направление) “возвращаются” эти точки в пространство (на соответствующие контурные линии фигур);

г) с помощью полученных точек определяется искомая тень, падающая от одной фигуры на другую.

ПРИМЕР.

На рис. 86 показано применение метода обратных лучей на

примере построения падающей тени от прямой на плоскость треугольника.

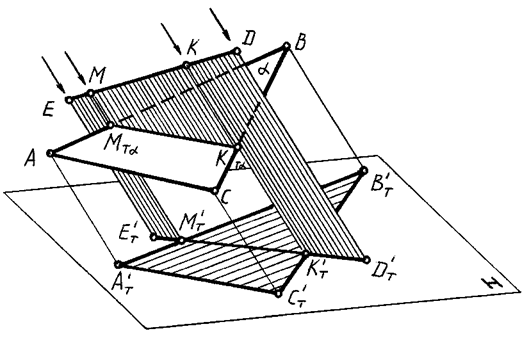
Рис. 86

Построены падающие тени от треугольника АВС и от прямой ED на плоскость Н. Через точки М _T' и М _T', общие теням прямой ED и сторонам АВ и ВС, проведены обратные лучи, пересекающие указанные прямые соответственно в точках М', М'', К' и K''. Точки М' и K' представляют собой тени от точек M'' и K'' прямой ЕD на стороны АВ и ВС. Искомая же тень будет определена точками M'K'.

На рис. 87 приведено решение этой задачи в ортогональных проекциях.

.

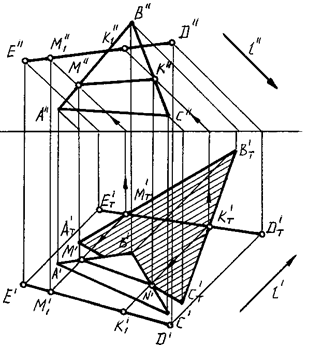
Рис. 87

2. Метод следа светового луча
(метод сечения лучевой плоскостью)

Метод следа луча основан на том, что тень, падающая от точки, есть след проведенного через нее луча.

На рисунке 88 приведено решение задачи на построение тени от прямой АВ на плоскость Q (CDEF) в ортогональных проекциях методом следа луча (или сечения лучевой плоскости).

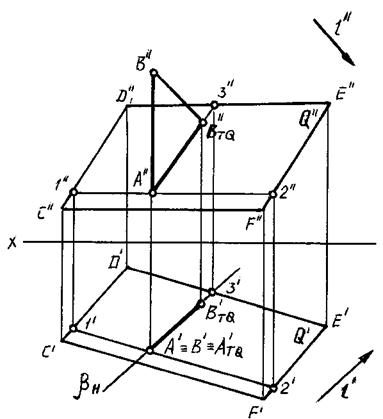
Рис. 88

В данном случае тень от прямой АВ на плоскость Q построена с помощью двух точек А _TQ(А _TQ', А _TQ'') и В _TQ(В _TQ', В _TQ''), в которых пересекаются с плоскостью Q(CDEF) соответственно данная прямая и световой луч, проходящий через точку В.

Плоскость b ^ H является лучевой плоскостью, которая проводится через луч ВВ _TQ для определения точки В _TQ(В _TQ', В _TQ'').

Date: 2015-04-23; view: 1008; Нарушение авторских прав