Квантовые числа электронов

Состояние каждого электрона в атоме обычно описывают с помощью четырех квантовых чисел: главного (n), орбитального (l), магнитного (m) и спинового (s). Первые три характеризуют движение электрона в пространстве, а четвертое - вокруг собственной оси.

Главное квантовое число (n). Определяет энергетический уровень электрона, удаленность уровня от ядра, размер электронного облака. Принимает целые значения (n = 1, 2, 3...) и соответствует номеру периода. Из периодической системы для любого элемента по номеру периода можно определить число энергетических уровней атома и какой энергетический уровень является внешним.

Пример.

Элемент кадмий Cd расположен в пятом периоде, значит n = 5. В его атоме электроны раcпределены по пяти энергетическим уровням (n = 1, n = 2, n = 3, n = 4, n = 5); внешним будет пятый уровень (n = 5).

Орбитальное квантовое число (l) характеризует геометрическую форму орбитали. Принимает значение целых чисел от 0 до (n - 1). Независимо от номера энергетического уровня, каждому значению орбитального квантового числа соответствует орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем, c одинаковыми n и l - подуровнем.

Для

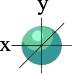
l=0 s- подуровень, s- орбиталь – орбиталь сфера

l=1 p- подуровень, p- орбиталь – орбиталь гантель

l=2 d- подуровень, d- орбиталь – орбиталь сложной формы

f-подуровень, f-орбиталь – орбиталь еще более сложной формы

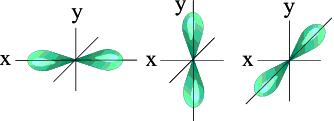s-орбиталь p- орбиталь

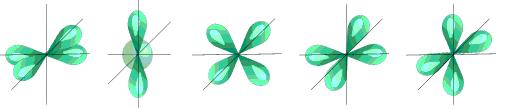d-орбиталь

На первом энергетическом уровне (n = 1) орбитальное квантовое число l принимает единственное значение l = (n - 1) = 0. Форма обитали - сферическая; на первом энергетическом только один подуровень - 1s. Для второго энергетического уровня (n = 2) орбитальное квантовое число может принимать два значения: l = 0, s- орбиталь - сфера большего размера, чем на первом энергетическом уровне; l = 1, p- орбиталь - гантель. Таким образом, на втором энергетическом уровне имеются два подуровня - 2s и 2p. Для третьего энергетического уровня (n = 3) орбитальное квантовое число l принимает три значения: l = 0, s- орбиталь - сфера большего размера, чем на втором энергетическом уровне; l = 1, p- орбиталь - гантель большего размера, чем на втором энергетическом уровне; l = 2, d- орбиталь сложной формы.

Таким образом, на третьем энергетическом уровне могут быть три энергетических подуровня - 3s, 3p и 3d.

Магнитное квантовое число (m) характеризует положение электронной орбитали в пространстве и принимает целочисленные значения от -I до +I, включая 0. Это означает, что для каждой формы орбитали существует (2l + 1) энергетически равноценных ориентации в пространстве.

Для s- орбитали (l = 0) такое положение одно и соответствует m = 0. Сфера не может иметь разные ориентации в пространстве.

Для p- орбитали (l = 1) - три равноценные ориентации в пространстве (2l + 1 = 3): m = -1, 0, +1.

Для d- орбитали (l = 2) - пять равноценных ориентаций в пространстве (2l + 1 = 5): m = -2, -1, 0, +1, +2.

Таким образом, на s- подуровне - одна, на p- подуровне - три, на d- подуровне - пять, на f- подуровне - 7 орбиталей.

Спиновое квантовое число (s) характеризует магнитный момент, возникающий при вращении электрона вокруг своей оси. Принимает только два значения +1/2 и –1/2 соответствующие противоположным направлениям вращения

Date: 2015-05-22; view: 569; Нарушение авторских прав