
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Изобарный
|
|
В изобарном процессе (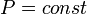 ):
):
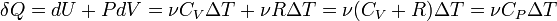
CP=δQ/νΔT=CV+R=((i+2)/2)*R
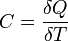
28. средняя энергия молекул идеального газа
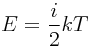
29. Распределение максвелла средняя скорость молекул
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью.
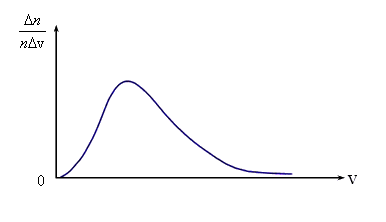 Рис. 3.3 Рис. 3.3
|
Задачу о распределении молекул по скоростям следует сформулировать следующим образом. Пусть в единице объема n молекул. Какая доля молекул 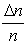 имеет скорости от v 1 до v 1 + Δ v? Это статистическая задача.
имеет скорости от v 1 до v 1 + Δ v? Это статистическая задача.
Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика. Необходимые измерения показали, что доля молекул 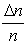 , отнесенная к интервалу скорости Δ v, т.е.
, отнесенная к интервалу скорости Δ v, т.е. 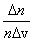 , имеет вид, показанный на рис. 3.3. Максвелл в 1859 г. теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла.
, имеет вид, показанный на рис. 3.3. Максвелл в 1859 г. теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла.
Аналитически она выражается формулой
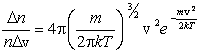 , ,
|
где m – масса молекулы, k – постоянная Больцмана.
Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.
Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
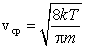
|
или
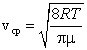 . .
|
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:
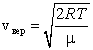 . .
|
3) среднюю квадратичную 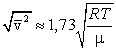 , – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная.
, – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная.
30. Опыт штерна
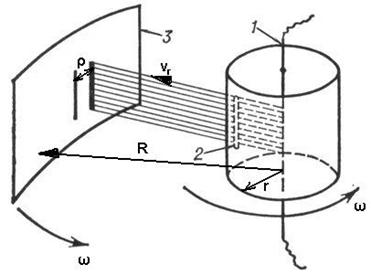 Экспериментальному подтверждению и визуализации распределения молекул газа по скоростям и был посвящен опыт Отто Штерна (1888–1969). Это еще один красивый опыт, позволявший в прямом смысле слова «начертить» график этого распределения на экспериментальной установке. Установка Штерна состояла из двух вращающихся полых цилиндров с совпадающими осями (см. рис. справа; большой цилиндр нарисован не полностью). Во внутреннем цилиндре, прямо по его оси была протянута серебряная нить 1, по которой пропускался ток, что приводило к ее нагреванию, частичному плавлению и последующему испарению атомов серебра с ее поверхности. В результате внутренний цилиндр, в котором изначально был вакуум, постепенно заполнялся газообразным серебром малой концентрации. Во внутреннем цилиндре, как показано на рисунке, была проделана тонкая щель 2, поэтому б о льшая часть атомов серебра, долетая до цилиндра, оседала на нем. Малая же часть атомов проходила сквозь щель и попадала во внешний цилиндр, в котором поддерживался вакуум. Здесь эти атомы уже не сталкивались с другими атомами и поэтому двигались в радиальном направлении с постоянной скоростью, достигая внешнего цилиндра через время, обратное пропорциональное этой скорости:
Экспериментальному подтверждению и визуализации распределения молекул газа по скоростям и был посвящен опыт Отто Штерна (1888–1969). Это еще один красивый опыт, позволявший в прямом смысле слова «начертить» график этого распределения на экспериментальной установке. Установка Штерна состояла из двух вращающихся полых цилиндров с совпадающими осями (см. рис. справа; большой цилиндр нарисован не полностью). Во внутреннем цилиндре, прямо по его оси была протянута серебряная нить 1, по которой пропускался ток, что приводило к ее нагреванию, частичному плавлению и последующему испарению атомов серебра с ее поверхности. В результате внутренний цилиндр, в котором изначально был вакуум, постепенно заполнялся газообразным серебром малой концентрации. Во внутреннем цилиндре, как показано на рисунке, была проделана тонкая щель 2, поэтому б о льшая часть атомов серебра, долетая до цилиндра, оседала на нем. Малая же часть атомов проходила сквозь щель и попадала во внешний цилиндр, в котором поддерживался вакуум. Здесь эти атомы уже не сталкивались с другими атомами и поэтому двигались в радиальном направлении с постоянной скоростью, достигая внешнего цилиндра через время, обратное пропорциональное этой скорости:
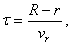
где 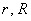 — радиусы внутреннего и внешнего цилиндров, а
— радиусы внутреннего и внешнего цилиндров, а 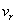 — радиальная компонента скорости частицы. В результате с течением времени на внешнем цилиндре 3 возникал слой серебряного напыления. В случае покоящихся цилиндров этот слой имел вид полоски, расположенной точно напротив щели во внутреннем цилиндре. Но если цилиндры вращались с одинаковой угловой скоростью
— радиальная компонента скорости частицы. В результате с течением времени на внешнем цилиндре 3 возникал слой серебряного напыления. В случае покоящихся цилиндров этот слой имел вид полоски, расположенной точно напротив щели во внутреннем цилиндре. Но если цилиндры вращались с одинаковой угловой скоростью 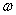 , то за время достижения молекулой внешнего цилиндра последний уже сдвигался на расстояние
, то за время достижения молекулой внешнего цилиндра последний уже сдвигался на расстояние
31. Распределение больцмана
Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.
Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.
Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа:
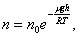
| (2.5.1) |
где n0 и n - число молекул в единичном объёме на высоте h = 0 и h.
32. Опыт перрена
До конца XIX в. реальность существования атомов и молекул не могла быть подтверждена из-за невозможности непосредственно их измерить и взвесить. Считалось, что атомно-молекулярное учение не отражает объективной реальности, а введено в науку для облегчения понимания химических процессов. Этим сомнениям был положен конец классическими опытами французского физика Перрена.
Он изготовил из смолистого вещества очень маленькие шарики, которые в его опытах играли роль моделей молекул газа. Шарики были приблизительно одинакового объема, и их массу можно было вычислить. Взболтав эти шарики в воде, Перрен наблюдал в микроскоп их распределение в сосуде. Вычислив количество шариков в единице объема на различных уровнях, ученый установил, что оно точно соответствует закону уменьшения концентрации газов с высотой. А этот закон был выведен из кинетической теории газов, в основе которой лежало атомно-молекулярное учение.
Date: 2015-05-22; view: 666; Нарушение авторских прав