Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Малые колебания - колебания, при которых возвращающая сила, действующая на тело, пропорциональна его отклонению от состояния равновесия
|
|
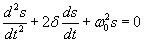
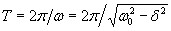
Если A(t) и A(t+Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
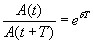
называется декрементом затухания, а его логарифм
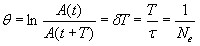
— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых во время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.
7. диф уравнение гармонических колебаний
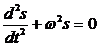 (2)
(2)
называется уравнением свободных гармонических колебаний (в дифференциальной форме).
8. Скорость ускорение гармонических колебаний
Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.
Согласно этому определению, закон изменения координаты в зависимости от времени имеет вид:

где wt - величина под знаком косинуса или синуса; w - коэффициент, физический смысл которого раскроем ниже; А - амплитуда механических гармонических колебаний.
9. Полная энергия гармонических колебаний
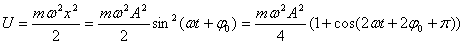
10. Примеры малых колебаний. Математический маятник.
Струны, стержни, мембраны, пластины Имеющие конечные размеры и закрепленные на краях.
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую изматериальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
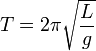
11. малые колебаний. Физический маятник.
Струны, стержни, мембраны, пластины Имеющие конечные размеры и закрепленные на краях.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейсяцентром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
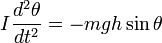 .
.
Полагая 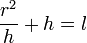 , предыдущее уравнение можно переписать в виде:
, предыдущее уравнение можно переписать в виде:
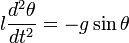 .
.
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 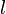 . Величина
. Величина 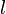 называется приведённой длиной физического маятника.
называется приведённой длиной физического маятника.
12. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
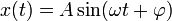
или
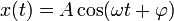 ,
,
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, 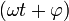 — полная фаза колебаний,
— полная фаза колебаний, 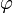 — начальная фаза колебаний.
— начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
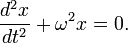
Здесь x – смещение тела от положения равновесия, x m – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ω t + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Физическая величина, обратная периоду колебаний, называется частотой колебаний:
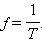
|
Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями:
|
13. Затухающие колебания
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.
Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.
Второй закон Ньютона в нашем случае запишется так:
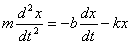
Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемом каноническом виде:
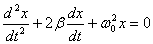
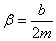 - коэффициент затухания,
- коэффициент затухания, 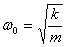 - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
- собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
14. Затухающие колебания логарифм. Декремент
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.
Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.
15. Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени. 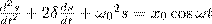 Решение уравнения (5) есть сумма общего решения однородного уравнения
Решение уравнения (5) есть сумма общего решения однородного уравнения
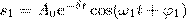 (12)
(12)
16. Резонанс
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность.
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
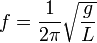 ,
,
17. Векторная диаграмма колебаний
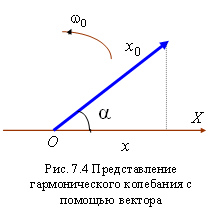
18. Существует очень наглядный геометрический способ представления гармонических колебаний, заключающийся в изображении колебаний в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой (рис. 7.4).
|
Выберем ось  . Из точки О, взятой на этой оси, отложим вектор длины
. Из точки О, взятой на этой оси, отложим вектор длины 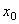 , образующий с осью угол
, образующий с осью угол 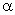 . Если привести этот вектор во вращение с угловой скоростью
. Если привести этот вектор во вращение с угловой скоростью 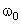 , то проекция конца вектора на ось
, то проекция конца вектора на ось 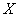 будет меняться со временем по закону
будет меняться со временем по закону 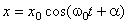 . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.
. Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.
Векторная диаграмма дает возможность свести сложение колебаний к геометрическому суммированию векторов. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:
|
 ,
,  .
.
Представим оба колебания с помощью векторов 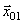 и
и 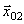 (рис. 7.5). Построим по правилу сложения векторов результирующий вектор
(рис. 7.5). Построим по правилу сложения векторов результирующий вектор 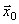 . Легко увидеть, что проекция этого вектора на ось
. Легко увидеть, что проекция этого вектора на ось 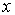 равна сумме проекций слагаемых векторов
равна сумме проекций слагаемых векторов 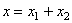 . Следовательно, вектор
. Следовательно, вектор 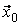 представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью
представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью 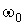 , что и векторы
, что и векторы 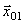 ,
, 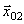 , так что результирующее движение будет гармоническим колебанием с частотой
, так что результирующее движение будет гармоническим колебанием с частотой 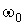 , амплитудой
, амплитудой 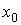 и начальной фазой
и начальной фазой 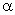 . По теореме косинусов квадрат амплитуды результирующего колебания будет равен
. По теореме косинусов квадрат амплитуды результирующего колебания будет равен
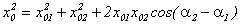 . .
| (7.3) |
Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна
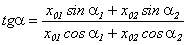 . .
| (7.4) |
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Формулы (7.3) и (7.4) можно, конечно, получить, сложив выражения для 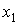 и
и 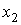 аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.
аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.
19. сложение взаимно перпендикулярных колебаний
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде
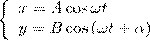 (1)
(1)
где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
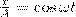
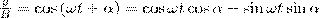
и заменяя во втором уравнении 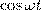 на
на  и
и 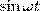 на
на 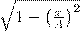 , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
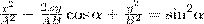 (2)
(2)
Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес:
1) α = mπ (m=0, ±1, ±2,...). В этом случае эллипс становится отрезком прямой
 (3)
(3)
где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой, которое совершается вдоль прямой (3), составляющей с осью х угол. В этом случае имеем дело с линейно поляризованными колебаниями;
2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид
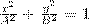 (4)
(4)
Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.
20. механические волны. виды волн
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.
21. уравнение плоской волны
В общем виде уравнение плоской волны записывается так:
22.
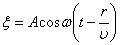 , или , или 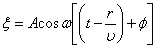 . .
|
23. Стоячие волны
Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фазаи коэффициент затухания волны в месте отражения.
Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе[1]; в природе — волны Шумана.
24. Идеальный газ
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекулможно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

25. Изопроцессы
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление,объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре —изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.
Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении (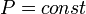 )
)
Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме (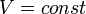 ). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
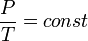
Линия, изображающая изохорный процесс на диаграмме, называется изохорой.
Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления. а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание.
Основная статья: Изотермический процесс
Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре (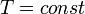 )(
)(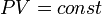 ). Изотермический процесс описывается законом Бойля — Мариотта:
). Изотермический процесс описывается законом Бойля — Мариотта:
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
Изоэнтропийный процесс — процесс изменения состояния термодинамической системы при постоянной энтропии (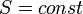 ). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:
). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:
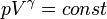
где 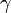 — показатель адиабаты, определяемый типом газа.
— показатель адиабаты, определяемый типом газа.
26. Первое начало термодинамики
Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
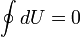
27. Теплоемкость идеального газа
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
Date: 2015-05-22; view: 869; Нарушение авторских прав