
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Магнитный момент и магнитная восприимчивость молекулы
|
|
Магнитный момент, векторная величина, характеризующая магнитные свойства вещества. Магнитным моментом обладают все элементарные частицы и образованные из них системы (атомные ядра, атомы. молекулы).
Метод магнитных моментов основан на взаимодействии вещества со статическим магнитным полем. Магнитную восприимчивость можно рассматривать как количественную меру отклика вещества на приложенное внешнее магнитное поле. Магнитное поле в вакууме характеризуется напряжённостью поля H. В образце, помещённом в магнитное поле, индуцируется собственное магнитное поле, совпадающее или не совпадающее по направлению с внешним полем. Поэтому эффективное магнитное поле внутри образца, называемое магнитной индукцией B, отличается от магнитного поля в вакууме и связано с ним соотношением (1):
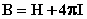 (1)
(1)
где I - интенсивность намагничивания или магнитный момент единицы объёма.
Из уравнения (1) следует, что B и H имеют одинаковую размерность, однако для того, чтобы подчеркнуть разницу между магнитным полем в вакууме и в реально среде, в системе SGSM единицу измерения H называют эрстедом (э), а единицу измерения B и I - гауссом (Гс).
Отношение магнитной индукции к напряжённости магнитного поля называют относительной магнитной проницаемостью ε' (аналог диэлектрической проницаемости). Отношение величин интенсивности намагниченности и напряжённости магнитного поля есть объёмная магнитная восприимчивость χv.
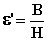
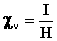
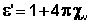
Объёмная магнитная восприимчивость безразмерна; в магнетохимии вместо неё используется удельная магнитная восприимчивость χg, размерность которой обратно размерности плотности (см3/г). Объёмная и удельная магнитные восприимчивости связаны между собой уравнением (2):
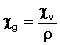 (2)
(2)
где ρ - плотность вещества.
Молярную магнитную восприимчивость χM, имеющую размерность см3/моль, находят по формуле (3):
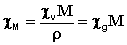 (3)
(3)
где M - молярная масса вещества.
Выражение для молярной магнитной восприимчивости напоминает уравнение для молярной поляризации (метод дипольных моментов) и также включает две составляющие (4):
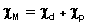 (4)
(4)
где χd - молярная диамагнитная восприимчивость (аналог деформационной поляризации), χp - молярная парамагнитная восприимчивость (аналог ориентационной поляризации).
Обе эти макросоставляющие связаны с соответствующими микроскопическими величинами уравнениями (5) и (5а): 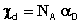
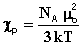
где χD - наведённая магнитная восприимчивость, приходящаяся на одну молекулу (аналог поляризуемости);
μo - постоянный магнитный момент (аналог дипольного момента);
NA - число Авогадро;
k - постоянная Больцмана;
Т - абсолютная температура.
Таким образом, выражение для молярной магнитной восприимчивости, связанной с молекулярными параметрами αD и μo, принимает следующий вид:
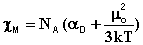 (6)
(6)
На этом, видимо, прекращается аналогия между магнитными и электрическими эффектами, поскольку χd и χp имеют различные знаки (χd<0, χp>0), в то время как соответствующие им электрические величины (деформационная и ориентационная поляризации) - одинаковые.
Если в магнитном поле находится вещество, молекулы которого не имеют неспаренных электронов, (μo = 0), то, в соответствие с уравнениями (4) и (6), единственным членом, дающим вклад в магнитную восприимчивость, является χd. В этом случае вещество является диамагнитным: оно менее проницаемо для магнитных силовых линий, чем вакуум, и в неоднородном магнитном поле на него действует сила, по направлению противоположная градиенту напряжённости магнитного поля. Иначе говоря, образец выталкивается из магнитного поля.
Если же молекулы помещённого в магнитное поле вещества содержат неспаренные электроны (свободные радикалы ионы переходным или редкоземельных элементов и т.п.), т.е. обладают отличным от нуля магнитным моментом, то положительная составляющая χp, превосходящая по абсолютной величине (не менее чем на порядок) отрицательную χd, делает магнитную восприимчивость χM положительной. В таком случае говорят, что вещество парамагнитно. Оно более проницаемо для магнитных силовых линий, и в нём индуцированное магнитное поле и внешнее поле совпадают по направлению. Образец вещества втягивается в магнитное поле.
Диамагнетизм присущ всем без исключения веществам и представляет собой сравнительно слабый эффект. Поэтому при выделении из χM парамагнитной составляющей (для вычисления магнитного момента) величиной χd часто пренебрегают.
В том случае, когда величину χd нужно учитывать, её определяют либо экспериментально по уравнению (6) из температурной зависимости магнитной восприимчивости, либо рассчитывают теоретически по аддитивной схеме Паскаля, которая будет рассмотрена ниже. В этом случае значение парамагнитной составляющей находят по формуле (7):
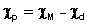 (7)
(7)
В химической литературе вместо χp часто используют иное обозначение - χ'M. Из уравнения (5) следует, что молярная магнитная восприимчивость, исправленная на диамагнетизм (χ'M), связана с температурой обратно пропорциональной зависимостью (8):
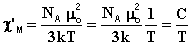 (8)
(8)
где C - константа Кюри.
Закон Кюри (8) не всегда выполняется, и чаще всего имеют место отклонения от него. В этом случае температурную зависимость магнитной восприимчивости описывает закон Кюри-Вейсса (9):
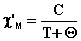 (9)
(9)
где Θ - константа Вейсса.
Нетрудно видеть, что константа Вейсса может быть найдена по температурной зависимости магнитной восприимчивости. Она может принимать как положительные, так и отрицательные значения; её размерность такая же, как у температуры, а величина чаще всего располагается в интервале 5 - 30 кельвинов. Физического смысла константа Вейсса не имеет. Отклонения от закона Кюри можно объяснить влиянием соседних парамагнитных частиц, так что в твёрдом теле или в концентрированном растворе, где плотность парамагнитных центров значительна, не следует ожидать выполнения закона Кюри.
Поскольку величина константы Вейсса не всегда известна (когда измерения проведены лишь при одной температуре), часто предполагают, что закон Кюри соблюдается, и определяют величину магнитного момента по уравнению (8). Для того чтобы указать на приближённый характер полученного значения, μo заменяют на μэфф - эффективный магнитный момент. За единицу измерения магнитного момента принимают магнетон Бора (μB, в русскоязычной литературе часто используется обозначение М.Б.):
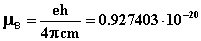
где е - заряд электрона;
h - постоянная Планка;
с - скорость света;
m - масса электрона.
Таким образом, эффективный магнитный момент, измеренный в магнетонах Бора, можно найти по формуле (10):
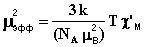 (10)
(10)
Благодаря случайному совпадению дробь в правой части выражения (10) почти точно равна восьми. Поэтому эффективный магнитный момент можно рассчитать по упрощённой формуле (11):
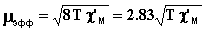 (11)
(11)
Формула (11) не учитывает температурно-независимый (ванфлековский) парамагнетизм (Nα). Величину Nα можно найти в справочной литературе; например, для иона Cu2+ Nα = 60·10-6 см3/моль. При учёте температурно-независимого парамагнетизма выражение (11) преобразуется к следующему виду:
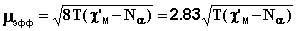
Date: 2015-05-22; view: 2047; Нарушение авторских прав