Метод конечных разностей

Лабораторная работа № 8

Цель работы: изучить применение метода конечных разностей для расчета балочных систем.

Порядок выполнения работы:

1) разбить балку на заданное число частей;

2) используя метод конечных разностей, определить изгибающие моменты и прогибы в сечениях балки; расчеты выполнить в системе компьютерной алгебры MathCAD;

3) построить эпюры моментов и прогибов балки.

Методика расчета. Для описания задач строительной механики и теории упругости часто используются дифференциальные уравнения равновесия, выражаемые через перемещения (прогибы) систем.

При обычном решении таких уравнений ищется функция перемещений, описывающая состояние системы и удовлетворяющая условиям задачи, включая её граничные условия.

В методе конечных разностей (МКР) находится не сама функция, а её значения в некоторых точках (узлах). Понятно, что густота разбивки системы
(λ = Δx) здесь определяет точность решения.

Дифференциальные уравнения равновесия для стержневых изгибаемых систем (рис. 8.1) могут быть представлены в трех вариантах [1]:

1) или (8.1)

2) 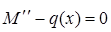, учитывая что (8.2)

3) 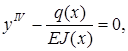получаемое путем дифференцирования уравнения (8.1) два раза c учетом выражения (8.2).

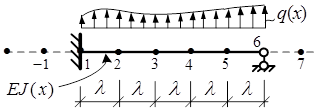
Рисунок 8.1

Производные определяющих выражений, представлены в [1].

При записи производных для граничных точек сооружений будут появляться так называемые законтурные точки (например, точки -1 и 7
на рис. 8.1), для определения «условных» перемещений в которых, используются граничные условия для сооружений, то есть известные значения физических величин на границах сооружения, связанные с условиями закрепления этих точек [1]:

1) шарнирное опирание (рис. 8.2):

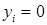и ;
Рисунок 8.2

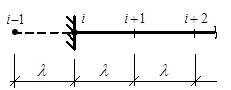
2) защемление (рис. 8.3):

и ;

Рисунок 8.3

Пример расчета. Рассмотрим применение метода конечных разностей к решению задач изгиба двухопорной балки, загруженной распределенной нагрузкой (рис. 8.4).

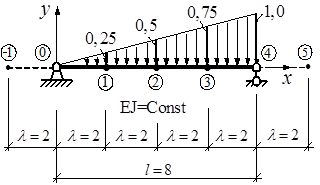
Рисунок 8.4

Воспользуемся вначале уравнением:

и определим изгибающие моменты в системе.

Заменяя производные конечными разностями, получим уравнение для произвольного i -го узла в виде:

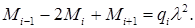(8.3)

Разобьем балку на четыре части (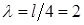) и составим уравнения (8.3) для точек 1,2 и 3 (последовательно принимая i равным номерам этих точек):

При этом согласно граничным условиям будем иметь: и .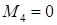

Решая эту систему уравнений, найдем:

; ; .

Для определения прогибов системы воспользуемся теперь уравнением:

.

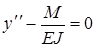В конечных разностях для произвольного i -го узла это уравнение будет иметь вид: 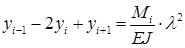. (8.4)

Записав уравнение (8.4) для точек 1,2 и 3, получим систему уравнений:

Решая систему уравнений с учетом граничных услови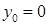й ( и ), найдем: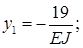

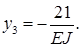
Построим эпюры изгибающих моментов и прогибов балки (рис. 8.5).

Рисунок 8.5

Расчеты произведем в системе компьютерной алгебры MathCAD.

Проанализировав результаты расчета, можно сделать следующие
выводы:

– в методе конечных разностей густота разбивки (сетки) системы определяет точность решения;

– при рассматриваемом нагружении балки наибольший ее прогиб возникает между точками 2 и 3.

Date: 2015-05-22; view: 1691; Нарушение авторских прав