Задание. Дифференцирование функций

Производной функции y=f(x) называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю

Правила:

1.

2.

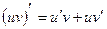
3.

4. Если y=f(u) и u=q(x) дифференцируемые функции своих аргументов, то производная сложной функции y=f(q(x)) существует и равна произведению производной данной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменой x.

.

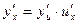Следствие: Постоянный множитель выносится за знак производной

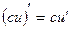
Формулы дифференцирования для сложной функции, где u(x) –внутренняя функция

Производной второго порядка или второй производной функции y=f(x) называется производная от ее первой производной функции 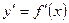. Она обозначается

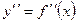. Аналогично определяются и обозначаются производные третьего, четвертого и других порядков

.

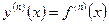Примеры: 1) Найти производную функции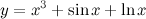

	Производная суммы равна сумме производных 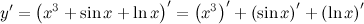Воспользуемся формулами из таблицы производных - формулы производных степенной, тригонометрической и логарифмической функций: , .
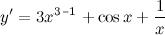Ответ.

2) Найти производную функции 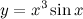. По правилу дифференцирования произведения получаем: 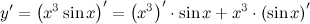, теперь воспользуемся формулами для производных степенной и тригонометрической функций: 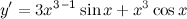, . Ответ: .

3) Найти производную функции

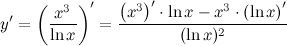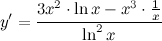
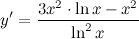
	По свойству дифференцирования частного получаем: Далее пользуясь формулами для производных логарифмической и степенной функции, получим: 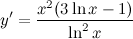Для вычисления производной функции использовались правила дифференцирования и таблица производных функций.
Ответ.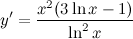

4) Правила дифференцирования сложной функции применяются следующим образом:

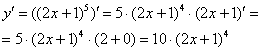
Уравнение касательной к графику функции у=f(x) в точке х₀=а

Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x₀ ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ^/ (x₀) · (x − x₀) + f (x₀)

Здесь f ^/ (x₀) — значение производной в точке x₀, а f (x₀) — значение самой функции.

Пример:

Дана функция y = x³. Составить уравнение касательной к графику этой функции в точке x₀ = 2.

Уравнение касательной: y = f ^/ (x₀) · (x − x₀) + f(x₀). Точка x₀ = 2 нам дана, а вот значения f (x₀) и f ^/ (x₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x₀) = f (2) = 2³ = 8;
Теперь найдем производную: f ^/ (x) = (x³) ^/ = 3x²;
Подставляем в производную x₀ = 2: f ^/ (x₀) = f ^/ (2) = 3 · 2² = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Физический смысл производной:

Если зависимость расстояния от времени представляет собой функцию S(x), то, чтобы найти скорость тела в момент времени t₀, нужно найти значение производной функции S(x) в точке х=t₀: S^/(t₀)=V(t); а чтобы вычислить значение ускорения в момент времени t₀, нужно найти значение производной функции V(x) в точке х=t₀: V^/(t₀)=a(t₀).

Пример. Материальная точка движется прямолинейно по закону s(t)=6t²-48t+17, где s(t)— расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9c.

Решение. Найдем производную функции s(t)=6t²-48t+17: s^/ (t) = 12t-48. Найдем значение производной в точке t=9: s^/ (9)=12*9-48, v(t)= s^/ (9)=60. Ответ: 60 м/с.

Решение тригонометрических уравнений:

Определение. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.

Простейшими тригонометрическими уравнениями являются уравнения вида

, , , .

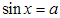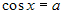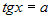Рассмотрим, при каких значениях 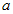тригонометрические уравнения разрешимы и как правильно находить все решения таких уравнений.