
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание: Предел функции
|
|
Методические рекомендации
Для выполнения контрольной работы №2
По математике 1 курс.
задание: Предел функции.
Число А называется пределом функции f(x) при 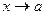 , если для любого числа
, если для любого числа 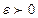 можно указать такое
можно указать такое 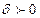 , что для любого
, что для любого 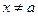 , удовлетворяющего неравенству
, удовлетворяющего неравенству 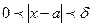 выполняется неравенство
выполняется неравенство  .
. 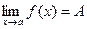 Функция f(x) называется бесконечно малой при
Функция f(x) называется бесконечно малой при 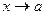 , если
, если 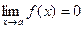 . Функция f(x) называется бесконечно большой при
. Функция f(x) называется бесконечно большой при 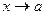 , если
, если 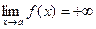 или
или 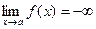 .
.
Свойства б/м и б/б функций:
· Если f(x) и g(x) – б/м при 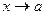 , то их сумма f(x) + g(x) при
, то их сумма f(x) + g(x) при 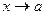 также является б/м.
также является б/м.
· Если f(x) - б/м при 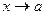 , а F(x) – ограниченная функция, то f(x)* F(x) есть функция б/м.
, а F(x) – ограниченная функция, то f(x)* F(x) есть функция б/м.
· Если при 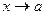 функция f(x) имеет конечный предел
функция f(x) имеет конечный предел 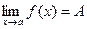 , а функция
, а функция 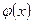 - б/б, то
- б/б, то 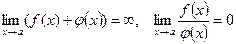 .
.
· Если f(x) - б/м при 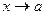 , то 1/ f(x) – б/б, причем в окрестности точки a функция f(x) в нуль не обращается.
, то 1/ f(x) – б/б, причем в окрестности точки a функция f(x) в нуль не обращается.
· Если f(x) - б/б при 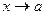 , то 1/ f(x) – б/м.
, то 1/ f(x) – б/м.
Теоремы о пределах.
1. Если f(x) имеет предел при 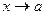 , то этот предел единственный.
, то этот предел единственный.
2. Предел суммы функций равен сумме пределов этих функций.
3. Предел произведения функций равен произведению пределов этих функций.
4. Предел частного двух функций равен частному пределов этих функций.
Следствия
5. Постоянный множитель можно выносить за знак предела 
6. Если n – натуральное число, то 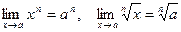 .
.
Замечательные пределы:
1) 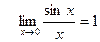 и
и 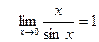 ;
;  и
и 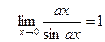 .
.
2) 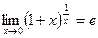 и
и 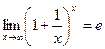 .
.
ПРИМЕР 1. Найти пределы функции:
а) 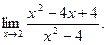 Решение: При
Решение: При 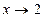 получаем неопределенность
получаем неопределенность 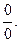 Сократим дробь
Сократим дробь
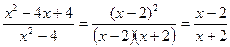 и вычислим
и вычислим 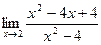 =
= 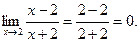
б) 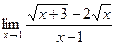 . Решение: При
. Решение: При 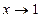 получаем неопределенность
получаем неопределенность 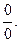 Сократим дробь, умножив числитель и знаменатель дроби на одно и тоже выражение, сопряженное числителю.
Сократим дробь, умножив числитель и знаменатель дроби на одно и тоже выражение, сопряженное числителю. 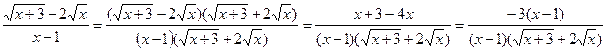 .
.
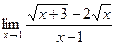 =
= 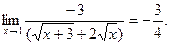
в) 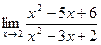 . Решение: При
. Решение: При 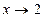 получаем неопределенность
получаем неопределенность 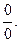 Сократим дробь, разложив числитель и знаменатель дроби на множители, найдя корни квадратного трехчлена.
Сократим дробь, разложив числитель и знаменатель дроби на множители, найдя корни квадратного трехчлена.
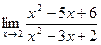 =
= 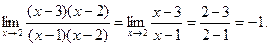
г) 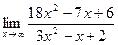 . При
. При  получаем неопределенность
получаем неопределенность 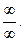
Решение: Сведем к бесконечно малым величинам, разделив каждое слагаемое числителя и знаменателя на наибольшую степень, т.е. х2.
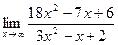 =
= 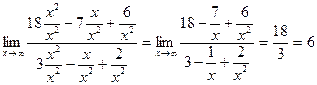 ,
,
так как при 
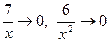 и т.д.
и т.д.
д) 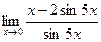 . Решение: Разобьем дробь на две дроби, применяя теоремы о пределах, и воспользуемся формулой первого замечательного предела
. Решение: Разобьем дробь на две дроби, применяя теоремы о пределах, и воспользуемся формулой первого замечательного предела
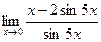 =
= 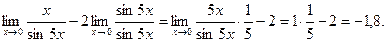
е) 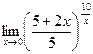 Решение: Разобьем дробь на две дроби и воспользуемся формулой второго замечательного предела.
Решение: Разобьем дробь на две дроби и воспользуемся формулой второго замечательного предела.
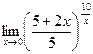 =
= 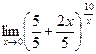 =
= 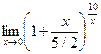 =
= 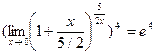 .
.
ж) 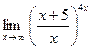 . Решение: Разобьем дробь на две дроби и воспользуемся одной из формул второго замечательного предела.
. Решение: Разобьем дробь на две дроби и воспользуемся одной из формул второго замечательного предела. 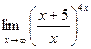 =
= 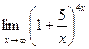 =
= 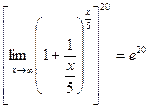 .
.
Date: 2015-05-22; view: 438; Нарушение авторских прав