
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

полного тензора напряжений массива пород
|
|
Поля тектонических напряжений гораздо менее однородны, чем поля гравитационных напряжений. Их параметры могут значительно изменяться как в пространстве, так и во времени. В частности, изменчивы ориентировка осей главных напряжений и их абсолютные значения. Поскольку в большинстве случаев тектонические напряжения действуют в горизонтальных или близких к ним направлениях, изменение тектонических напряжений по глубине может быть охарактеризовано вертикальным градиентом тектонических сил Dsт, выражающим зависимость максимального главного горизонтального сжимающего напряжения от глубины.
Градиент Dsт в общем случае является переменной величиной, зависящей от строения массива и рельефа земной поверхности.
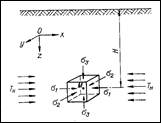
Рассматривая напряженное состояние какого-либо элементарного объема в массиве (рис. 4.4), подверженном действию горизонтальных тектонических сил, можно утверждать что одно из главных нормальных горизонтальных напряжений численно
|
Рис. 4.4 Схема к расчету параметров поля напряжений при действии горизонтальных тектонических сил.
равно:
s1 = Тн, (4.4)
где Тн - горизонтальное тектоническое напряжение в рассматриваемом массиве.
Для напряжений s3 и s2 справедливы следующие соотношения:
s3 = c Тн; s2 = y Тн, (4.5)
причем
n n
--------- > c³ 0; --------- > y ³ n. (4.6)
1 - n 1 - n
Поскольку гравитационные напряжения в массиве всегда имеют место, в случае действия тектонических сил напряжённое состояние массива будет определяться суммой двух тензоров:
Т s = Т s Г + Т sТ (4.7)
где Т sГ,Т sТ - тензоры напряжений, обусловленные соответственно действием гравитационного и тектонического полей напряжений.
В свою очередь Т sГ равняется
| s1Г | x g H | или при | g H | |||||||
| s2Г | или | x g H | гидростати- | g H | ||||||
| s3Г | g H | ческом поле | g H |
Тензор тектонических напряжений Т sТ для какой-либо точки массива, расположенной на глубине H от дневной поверхности, имеет вид
| s1Т | Т0 + DsтН | |||||
| s2Т | или | y (Т0 + DsтН) | ||||
| s3Т | c (Т0 + DsтН) |
где То -значение горизонтальных тектонических напряжений на уровне дневной поверхности (или другой плоскости отсчета глубины).
Как следует из выражения (4.7), тензор тектонических напряжений может быть получен как разность экспериментально определенного полного тензора напряжений и расчетного тензора гравитационных напряжений на той же глубине.
В заключение необходимо высказать ряд замечаний общего характера.
Прежде всего, рассматривая действие гравитационных и тектонических полей мы не упоминали влияния параметра “время” на состояние конкретных массивов пород.
Однако в литературе неоднократно высказывались мнения о влиянии реологических процессов на формирование начальных полей напряжений породных массивов. При этом в большинстве случаев считалось, что в результате релаксации напряжений за весьма длительный период существования массива начальное поле имеет тенденцию к выравниванию и таким образом негидростатические поля трансформируются в гидростатические, т.е. равнокомпонентные. Однако, результаты непосредственных измерений компонент напряжений в натурных условиях не подтверждают подобной тенденции, по-видимому подобное положение может проявляться только в отдельных конкретных ситуациях.
Если же вспомнить о иерархично-блочной структуре массивов горных пород, то логично было бы предположить, что подобную иерархично-блочную структуру должно иметь и начальное поле напряжений. При этом, поскольку гравитационное поле действует повсеместно и определяется плотностными свойствами и глубиной рассматриваемой точки от дневной поверхности, по-видимому именно тектоническая составляющая обусловливает иерархичность общего поля естественных напряжений массива пород.
Тогда, величины действующих начальных напряжений в каком-либо конкретном структурном блоке массива пород (а о точке массива в данном случае говорить уже некорректно) будут определяться его положением в системе других блоков более низкого ранга и параметрами напряжённого состояния на границах структурных блоков каждого из более низких рангов. Вполне естественно, что задача определения начального напряжённого состояния при такой постановке становится весьма сложной, хотя некоторые результаты, подтверждающие высказанные предположения, в последнее время уже появились.
В частности, по современным представлениям выделяются поля напряжений различного масштабного уровня или ранга: глобальные, региональные, локальные и частные (табл.4.2).
Характеристика полей напряжений различных рангов.
Таблица 4.2..
| Ранг | Наименование поля напряжений | Определяющие факторы |
| Глобальные | Общее увеличение объёма Земли Изменение формы и положения оси вращения планеты. Космические факторы. | |
| I | Региональные | Латеральные потоки астеносферы. Образование новых рифтов. Смена направления движения плит. Взаимодействие литосферных плит (субдукция, столкновение плит, скольжение или сдвиг плит). |
| II | Локальные | Рельеф поверхности. Вертикальные движения блоков. Разломы, складки, деформации пачек слоёв. |
| III | Частные | Трещиноватость, слоистость. Деформации слоя пород, раздувы, пережатия. Свойства пород. |
| IV | Точечные | Деформации зеёрен. Образование микротрещин. |
Глобальные поля напряжений характерны для крупнейших структур - типа континентов и океанических впадин, т.е. для структурных элементов самого низкого ранга.
Региональные поля напряжений соответствуют следующему типу структурных элементов - литосферным плитам и крупным коровым разломам.
Локальные и частные поля напряжений формируются в структурных блоках меньшего уровня, и, наконец точечные поля соответствуют уровню кристаллических зёрен или, другими словами, структурных неоднородностям самого высшего уровня.
Однако при этом необходимо заметить, что в настоящее время ещё недостаточно данных, чтобы уверенно говорить о количественных характеристиках выделенных рангов полей напряжений. Пока можно лишь утверждать, что по мере уменьшения структурных блоков или, другими словами, при переходе к более высоким порядкам структурных неоднородностей, поля напряжений становятся более неоднородными, а следовательно, возрастают величины касательных напряжений.
4.4. Особенности напряжённо-деформированного состояния грунтовых массивов.
Напряжённое состояние грунтовых массивов определяется только гравитационным полем напряжений. Вследствие этого вертикальная компонента по горизонтальным площадкам определяется, как и в случае массивов горных пород
H
s3 = S gi hi (4.8)
0
где gi - объемный вес i-го слоя пород; hi - мощность i-го слоя; Н - глубина рассматриваемой точки от дневной поверхности.
Однако в отличие от массивов горных пород напряжённо-деформированное состояние грунтов определяется не только деформируемостью твердых частиц (породного скелета), но и изменением объема пор при сжатии, которое сопровождается отжатием из грунта поровой воды.
В грунтовом массиве при его естественном состоянии гравитационное давление от массы пород PZ уравновешивается внутренним напряжением породного скелета Рэ0 и исходным давлением поровой жидкости Рн0:
PZ = γср Н = Рэ0 + Рн0, (4.9)
где γср — средняя плотность пород, т/м3; Н — высота столба пород над рассматриваемой точкой, м.
Исходное давление поровой жидкости равно
Рн0 = γв Н, (4.10)
где γв — плотность воды, т/м3.
Если давление поровой жидкости уменьшается или снимается вообще, величина напряжений в породном скелете Рэ0 увеличивается и может быть определена из выражения:
Рэ0 = PZ - Рн0 = γср Н – γв Н, (4.11)
Величины горизонтальных компонент поля напряжений в грунтовых массивах определяются в основном типом слагающих пород. В галечных, гравелистых и песчаных грунтовых массивах можно считать, что
s1 = s2 = x s3 = s3 (1 – sin j) / (1 + sin j) (4.12)
В глинистых грунтовых массивах величину бокового отпора можно полагать x = 1.
Всё сказанное свидетельствует о том, что проблема определения естественных или начальных полей напряжений массива горных пород является чрезвычайно важной для геомеханики и пока ещё достаточно далека от своего решения.
Date: 2015-05-22; view: 770; Нарушение авторских прав