Частицы и античастицы

Уравнение Шредингера не удовлетворяет требованиям теории относительности — оно не инвариантно по отношению к преобразованиям Лоренца. В 1928 г. английскому физику П. Дираку удалось найти релятивистское волновое уравнение. Из решения этого уравнения естественным образом, без каких-либо дополнительных предположений, получается спин и численное значение собственного магнитного момента электрона. Таким образом, выяснилось, что спин представляет собой величину одновременно и квантовую, и релятивистскую.

Уравнения Дирака позволило также предсказать существование античастицы электрона — позитрона. Из этого уравнения получаются для полной энергии свободной частицы не только положительные, но и отрицательные значения. Исследование уравнения показывает, что при заданном импульсе частицы р существуют решения уравнения, соответствующие энергиям:

Е =± 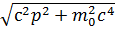. Между наименьшей положительной энергией (+ m ₀ с ²) и наибольшей отрицательной (— m ₀ с ²) имеется интервал значений энергии, которые не могут реализоваться. Ширина этого интервала равна

2 m ₀ с ² (рис.13.2). Таким образом, получаются две области собственных значений энергии: одна начинается с + m ₀ с ² и простирается до +∞, другая начинается с — m ₀ с ² и простирается до —∞. В неквантовой релятивистской механике энергия выражается через импульс и формально также может иметь отрицательные значения. Однако энергия изменяется непрерывно и поэтому не может пересечь запрещенную зону и перейти от положительных значений к отрицательным. В квантовой теории энергия может изменяться не только непрерывно, но и скачком, так что существование запрещенной зоны не может воспрепятствовать переходу частицы в состояния с отрицательной энергией. Частица с отрицательной энергией должна обладать весьма странными свойствами. Переходя в состояния со все меньшей энергией (т. е. с увеличивающейся по модулю отрицательной энергией), она могла бы выделять энергию, скажем, в виде излучения, причем, поскольку | E | ничем не ограничен, частица с отрицательной энергией могла бы излучить бесконечно большое количество энергии. Из соотношения Е=mс ² вытекает, что у частицы с отрицательной энергией масса будет также отрицательна. Под действием тормозящей силы частица с отрицательной массой должна не замедляться, а ускоряться, совершая над источником тормозящей силы бесконечно большое количество работы. Ввиду этих трудностей следовало, казалось бы, признать, что состояния с отрицательной энергией нужно исключить из рассмотрения как приводящие к абсурдным результатам. Это, однако, противоречило бы некоторым общим принципам квантовой механики. Поэтому Дирак предположил, что переходы электронов в состояния с отрицательной энергией обычно не наблюдаются по той причине, что все имеющиеся уровни с отрицательной энергией уже заняты электронами (электроны, как и другие частицы с полуцелым спином, подчиняются принципу Паули, который запрещает находиться в одном и том же состоянии более чем одной частице). Согласно Дираку вакуум есть такое состояние пространства, в котором все уровни отрицательной энергии заселены электронами, а уровни с положительной энергией свободны (рис.13.3, а). Поскольку заняты все без исключения уровни, лежащие ниже запрещенной полосы, электроны на этих уровнях никак себя не обнаруживают. Подобно этому в диэлектрике электроны, полностью заполняющие валентную зону, никак не реагируют на действие электрического поля. Если одному из электронов, находящихся на отрицательных уровнях, сообщить энергию, превышающую ширину запрещенной зоны, равную 2 m ₀ с ², то
этот электрон перейдет в состояние с положительной энергией и будет вести себя обычным образом, как частица с положительной массой и отрицательным зарядом. Вакансия («дырка»), образовавшаяся при этом в совокупности отрицательных уровней, должна вести себя как электрон, имеющий положительный заряд. Действительно, отсутствие частицы, обладающей отрицательными массой и зарядом, будет восприниматься как наличие частицы с положительной массой и положительным зарядом. Эта первая из предсказанных теоретически частиц была названа позитроном.

При встрече позитрона с электроном они аннигилируют (исчезают) — электрон переходит с положительного уровня на вакантный отрицательный). Энергия, соответствующая разности этих уровней, выделяется в виде излучения. На рис.13.3, б стрелка 1 изображает процесс рождения пары электрон — позитрон, а стрелка 2 — их аннигиляцию.

Прежде чем аннигилировать, электрон и позитрон образуют метастабильную связанную систему, аналогичную атому водорода, в котором протон заменен позитроном. Такое связанное состояние электрона и позитрона называется позитронием. В зависимости от значения результирующего спина этой системы различают парапозитроний (у которого S = 0, т. е. спины е^- и е⁺ антипараллельны) и ортопози-
троний (S = 1, спины е^- и е⁺ параллельны). Время жизни равно для парапозитрония ~ 10^-10с, для ортопозитрония ~ 10^-7с. Вследствие аннигиляции электрона и позитрона позитроний распадается на фотоны,
суммарная энергия которых равна 2 m ₀ с ² = 1,02 МэВ.

Теория Дирака была настолько «сумасшедшей», что большинство физиков отнеслось к ней весьма недоверчиво. Однако в 1932 г. американский физик К. Андерсон обнаружил позитрон в составе космических лучей. Рождение электронно-позитронных пар происходит при прохождении γ-фотонов через вещество. Это один из основных процессов, приводящих к поглощению γ-лучей веществом. Для соблюдения закона сохранения импульса в процессе рождения пары должна участвовать еще одна частица (ядро или электрон), которая воспринимает избыток импульса γ-фотона над суммарным импульсом электрона и позитрона. Следовательно, процесс запишется в виде уравнения:

γ+ Х → Х + е ^- + е ⁺, (13.1)

где X — ядро, в силовом поле которого происходит рождение пары. При аннигиляции требования закона сохранения импульса удовлетворяются тем, что возникают два или три γ-фотона, разлетающихся в разные стороны:

е ^-+ е ⁺→γ + γ(+ γ). (13.2)

Электронно-позитронные пары могут также возникать при взаимодействии γ-фотона с электроном:

γ + е ^- → е^-+е^-+ е⁺, (13.3)

и при столкновениях между двумя заряженными частицами, например электронами:

е^-+е^-→ е^-+е^-+ е^-+е⁺. (13.4)

Доля энергии, получаемая ядром X в ходе процесса (13.1), столь мала, что порог реакции образования пар (т. е. необходимая для этого минимальная энергия γ-фотона) практически равен 2 m ₀ с ² (масса электрона равна массе позитрона). Порог реакции (13.3) составляет 4 m ₀ с ², а реакции (13.4) — 7 m ₀ с ². Таким образом, требования одновременного сохранения энергии и импульса приводят к тому, что порог реакции (минимальная энергия исходных частиц) может оказаться заметно больше, чем суммарная энергия покоя рождающихся частиц.

Уравнение Дирака применимо не только к электронам и позитронам, но и к другим частицам со спином 1/2. Следовательно, для каждой такой частицы должна существовать античастица. По аналогии с (13.4) рождения пары протон —антипротон (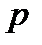 — 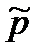) или нейтрон — антинейтрон (n — 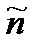) можно было ожидать при столкновении нуклонов достаточно большой энергии.

Антипротон отличается от протона знаком электрического заряда и собственного магнитного момента (у антипротона магнитный момент отрицателен, т. е. направлен противоположно механическому моменту). Главное же, что отличает антипротон от протона (и вообще частицу от античастицы), заключается в их способности к взаимной аннигиляции, в результате которой возникают другие частицы (в случае 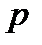— 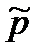преимущественно π-мезоны). Антипротон может аннигилировать при
встрече не только с протоном, но и с нейтроном. Совокупность возникающих частиц в отдельных актах аннигиляции различна.

При аннигиляции 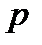— 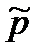в среднем рождается около пяти π-мезонов, из которых примерно три заряженных и два нейтральных.

В 1956 г. Б. Корком, Г. Ламбертсоном, О. Пиччони и В. Вензелем наблюдались антинейтроны, которые получались перезарядкой антипротонов, т. е. в результате процесса: .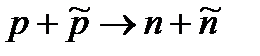

Антинейтрон отличается от нейтрона знаком собственного магнитного момента (у антинейтрона направление магнитного момента совпадает с направлением механического момента) и способностью аннигилировать при встрече с нуклоном (нейтроном или протоном). В результате аннигиляции рождаются новые частицы (главным образом π-мезоны).

Античастицы имеются не только у фермионов, но и у бозонов. Так, например, π⁺-мезон является античастицей по отношению к π^--мезону. Известны только четыре частицы, которые тождественны со своими античастицами (т. е. не имеют античастиц). Это — фотон, π°-мезон
и два К⁰-мезона (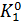 и 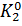). Такие частицы называются абсолютно нейтральными. Частицы, тождественные со своими античастицами, не способны к аннигиляции.

Если барионам, в том числе и нуклонам, приписать барионный заряд (или барионное число) В = +1, а антибарионам — барионный заряд

В = —1, то для всех процессов, протекающих с участием барионов и антибарионов, будет характерно сохранение барионного заряда.

Закон сохранения барионного заряда обусловливает стабильность самого легкого из барионов— протона. Другие законы сохранения (энергии, импульса, момента импульса, электрического заряда и т. п.) не запрещают, например, процесса 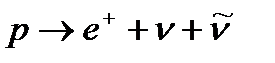, который в конечном итоге привел бы к аннигиляции атомов. Однако такой процесс сопровождался бы уменьшением барионного заряда на единицу и поэтому не наблюдается. Аналогично, закон сохранения электрического заряда обусловливает стабильность самой легкой заряженной частицы — электрона, запрещая процесс: .

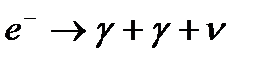Для объяснения особенностей протекания процессов с участием лептонов вводят квантовое число L - лептонный заряд или лептонное число. Лептонам приписывается L = +1, антилептонам L = —1, всем остальным частицам L = 0. Во всех без исключения процессах наблюдается сохранение суммарного лептонного заряда рассматриваемой системы.

Преобразование всех величин, описывающих физическую систему (волновых функций, уравнений и т. п.), при котором все частицы заменяются античастицами (например, электроны позитронами, а позитроны электронами и т. д.), называется зарядовым сопряжением. Какую из двух зарядово-сопряженных частиц считать частицей, а какую — античастицей, является делом чисто условным. Однако, сделав выбор для одной пары зарядово-сопряженных частиц, выбор для других пар нужно делать так, чтобы в наблюдающихся взаимодействиях сохранялись барионный и лептонный заряды. Принято считать электрон и протон частицами, а позитрон и антипротон — античастицами. При этом условии выбор для остальных барионов и лептонов делается однозначным. Результаты, к которым приводит учет требований сохранения В и L, приведены в табл. 13.1. Лептонное число электрона и нейтрино равно +1, а позитрона и антинейтрино —1. Поэтому электрон может возникать вместе с антинейтрино, а позитрон — вместе с нейтрино.

Таблица 13.1

	Частицы		Античастицы
Барионы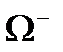
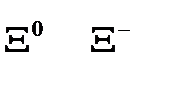
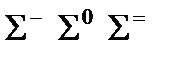
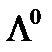
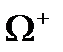
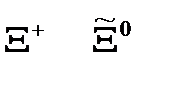
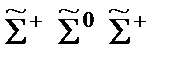
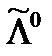
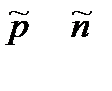
Мезоны	К + К 0
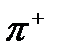
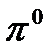
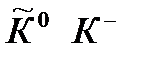
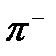
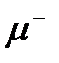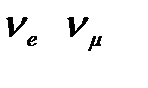
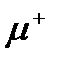Лептоны	е -		е +
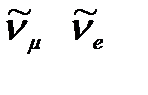
Фотон		γ

Приписав электрону L = +1, мы должны отрицательному мюону также приписать L = +1, т. е. считать частицей, а положительный мюон рассматривать как античастицу, и приписывать ему значение L = —1.

Date: 2015-05-19; view: 1222; Нарушение авторских прав