Законы сохранения в микромире

Важной проблемой в теории движения и протекания всевозможных реакций столкновений и превращений микрочастиц являются законы сохранения, которые утверждают постоянство некоторых параметров в природе и, в частности, в микромире. Законы классической физики чаще всего имеют вид законов изменения чего-нибудь, а не сохранения или постоянства, хорошим примером чего являются законы динамики Ньютона, которые описывают реакцию тел на действующие силы; другим примером могут служить законы электромагнетизма Фарадея-Максвелла.

Но постепенно законы сохранения приобрели главенствующее значение среди законов природы. Этому способствовали две причины: во-первых, связь таких законов с характером симметрии пространства-времени и, во-вторых, необходимость наведения порядка в хаосе, который наблюдался в процессах превращения микрочастиц в результате различных взаимодействий. Резюмируя, можно сказать, что старая физика интересовалась более законами дозволения, которые гласили, что может (и должно) произойти с телами в природе. Согласно же новой точке зрения, наиболее фундаментальными законами природы стали законы, которые носят характер запретов, определяя то, что не может происходить в природе. Заметим, что некоторые величины в природе абсолютно постоянны и не изменяются, а есть и такие, которые сохраняются лишь при определенных типах процессов, при других их постоянство нарушается.

Остановимся на перечислении и обсуждении семи законов сохранения, которые господствуют в современной микрофизике и являются абсолютно строгими - это законы сохранения:

1) энергии;

2) импульса;

3) момента количества движения (момента импульса);

4) электрического заряда;

5) электронного лептонного заряда;

6) мюонного и тау-лептонного заряда;

7) барионного заряда.

Первые три закона сохранения связаны со свойствами движения микрочастиц в пространстве-времени, следующие четыре закона должны быть отнесены к внутренним свойствам микрочастиц. Напомним, что первые четыре закона сохранения, приведенные в списке, были уже известны в макрофизике.

Рассмотрим некоторые реакции распадов микрочастиц, иллюстрирующие разные законы сохранения. Например, закон сохранения электрического заряда выполняется при таких реакциях распада:

,

,

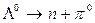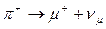а также в реакции на встречных пучках протонов в ускорителе микрочастиц:

.

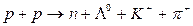Далее, закон сохранения электрического заряда объясняет тот факт, что элементарные частицы имеют заряд, кратный электронному заряду е. Дробные заряды в единицах е, например 0,65 е, затруднили бы подведение баланса заряда в превращениях и поддержании постоянства величины заряда. Наиболее важным следствием закона сохранения заряда является устойчивость электрона. Электрон - самая легкая микрочастица, она могла бы распадаться только на еще более легкие частицы: фотон, нейтрино, гравитон. Однако тогда произошло бы нарушение закона сохранения заряда. Если этот закон был не вполне строгим, то электроны должны были бы иметь конечное и малое время жизни. Но по имеющимся оценкам, оно практически бесконечно и составляет 10¹⁹ лет, т.е. электрон является устойчивой микрочастицей, как и протон.

В отличие от первых перечисленных выше четырех законов сохранения, которые были известны и в классической физике, последние три закона, приведенные в списке, были установлены при изучении превращений микрочастиц в последнее время. Например, число барионов (т.е. величина барионного заряда) сохраняется в реакция такого типа:

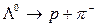и .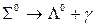

При столкновении двух протонов суммарное число барионов равно двум, и реакция имеет вид:

.

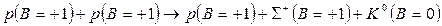Именно закон сохранения числа барионов дает для протона абсолютную устойчивость со временем - его время жизни в миллион миллиардов раз больше, чем возраст Земли т.е. 10²⁷ лет. Закон сохранения числа барионов выполняете когда в реакции взаимодействия участвуют и антибарионы с В = - 1, например, в такой реакции:

.

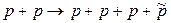Здесь слева стоят микрочастицы с В =+1 и В =+1, а справа с В =+1, В =+1 и В = +1, В =-1.

Законы сохранения одновременно электрического и лептонного зарядов, например, выполняются в реакции:

.

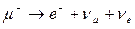Перейдем теперь к рассмотрению законов сохранения величин, являющихся свойствами движения микрочастиц в пространстве-времени. Так, закон сохранения энергии требует, чтобы суммы масс покоя в правой и в левой сторонах равенства различались и в правой части сумма была меньше, чем в левой. Примером таких реакций могут служить следующие процессы (здесь массы покоя даются в энергетических единицах МэВ)

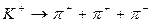
и для масс покоя:

.

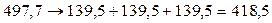Или:

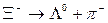
и для масс покоя

.

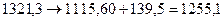Далее,

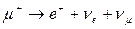
и для масс покоя

.

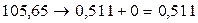Закон сохранения импульса можно проиллюстрировать реакцией распада покоящегося К ⁺ каона:

,

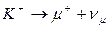при этом мюон и нейтрино разлетаются в разные стороны, как показано на рис. 2 (стрелками показаны импульсы разлетающихся в противоположные стороны частиц). Данный закон категорически запрещает, чтобы одна микрочастица превратилась в другую микрочастицу без появления еще одной. Например, невозможна такая реакция:

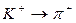
хотя здесь могут соблюдаться законы сохранения энергии и электрического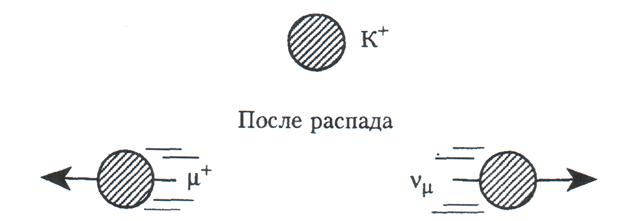

Рис. 2. Иллюстрация применения закона сохранения импульса к процессу распада покоящегося каона К⁺ на мюон μ⁺ и мюонное нейтрино ν_μ.

заряда. Однако разность масс покоя каона К⁺ и пиона π ⁺ (в энергетических единицах МэВ у каона она равна 439,71 и у пиона 139,5) должна превратиться в кинетическую энергию продукта распада, т.е. пиона, с которой обязательно связано появление у него импульса. Поэтому, чтобы сумма импульсов

по-прежнему равнялась нулю, должно быть два объекта распада, разлетающихся в разные стороны с противоположно направленными и равными по величине импульсами. Поскольку справа в реакции стоит только один пион π ⁺, то он будет двигаться и обладать ненулевым импульсом, что противоречит закону сохранения импульса, поскольку импульс покоящегося каона К ⁺ равен нулю. Если же приписать пиону π ⁺ импульс, равный нулю, то нарушается закон сохранения масс покоя или энергии, что невозможно. Проиллюстрируем еще применение закона сохранения момента количества движения. Пусть пион π ⁺, не имеющий спина, распадается на мюон μ ⁺ и нейтрино v_μ со спином, равным 1/2. Этот процесс возможен только при антипараллельных спинах мюона μ ⁺ и нейтрино v_μ, тогда суммарный момент количества движения равен нулю.

Приведем еще один пример распада покоящегося гиперона 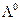со спином 1/2 (рис. 4а,б):

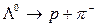
Такой распад может происходить двумя способами. При первом протон р и пион π^- не имеют орбитальных моментов, а спин протона параллелен спину гиперона (рис. 4а). Второй вариант процесса распада: спин протона антипараллелен спину гиперона, но пион имеет единичный момент количества движения, который направлен параллельно спину гиперона (рис. 4б). В обоих случаях суммарные моменты количества движения начальной и конечных частиц одинаковы.

Рис. 3. Иллюстрация применения закона сохранения момента количества движения для распада гиперона 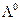: а)первый момент распада, когда спин гиперона 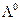протона p параллельны, а спин пиона π^- равен нулю; б)второй вариант распада: спин гиперона 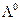и протона р антипараллельны, но есть единичный момент.

Первым из исторически известных нам процессов распада микрочастиц был бета-распад, он прекрасно иллюстрирует все обсуждаемые законы сохранения. Эта реакция, неоднократно приводимая выше, имеет вид:

,

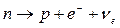она изображена на рис. 4. При бета-распаде сохраняется энергия, ибо сумма масс покоя протона (938, 956 МэВ), электрона (0,511 МэВ) и антинейтрино (0) меньше массы покоя нейтрона (939,550 МэВ). Сохраняется также импульс: три частицы разлетаются в разные стороны, причем избыток энергии будет распределяться между ними так, чтобы сумма трех векторов импульса обращалась в нуль (поскольку импульс нейтрона до распада ядра атома был равен нулю). Выполняется и закон сохранения момента количества движения, показанный на рис. 4, - электрон (е ^-) и протон (р) разлетаются в разные стороны с антипараллельными спинами, а спин антинейтрино направлен параллельно и равен по величине спину исходной микрочастицы, т.е. нейтрона. Электрические заряды протона и электрона нейтрализуются, антинейтрино имеет нулевой электрический заряд, - суммарный электрический заряд у продуктов реакции равен нулю. Электронный, мюонный и тау-типа лептонные заряды у протона и нейтрона отсутствуют, у электрона и антинейтрино отличны от нуля только электронные лептонные заряды, но они разного знака и поэтому в сумме дают нуль. Наконец, барионный заряд В =+1 у протона и нейтрона и равен нулю у электрона и антинейтрино.

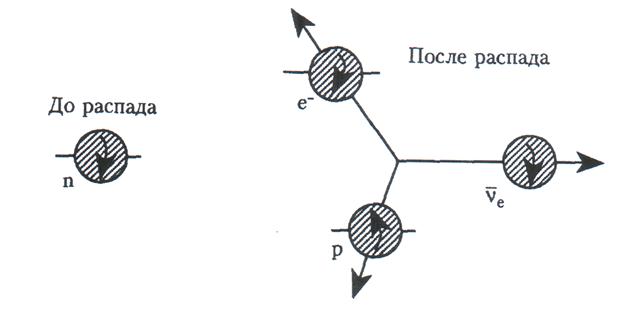
Рис. 4. Иллюстрация выполнения законов сохранения

Date: 2015-05-19; view: 8421; Нарушение авторских прав