Введение. Исполнитель Макарова Наталья Геннадьевна, студент 3 курса, группа ТН-10

КУРСОВАЯ РАБОТА

по дисциплине КВАНТОВАЯ МЕХАНИКА

на тему КВАНТОВАЯ ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ

Исполнитель Макарова Наталья Геннадьевна, студент 3 курса, группа ТН-10

Руководитель Вострокнутова Ольга Николаевна, ст. пр. каф. Физики

Работа допущена к защите «____» ___________20___г. _________

Работа защищена «____» ___________20___г. с оценкой ____________ ________

Магнитогорск

2012 г.

Содержание

1. Введение. 3

2. Уравнение Шрёдингера. 4

3. Квантовая частица в потенциальной яме. 7

3.1 Квантовая частица в потенциальной яме бесконечной глубины.. 9

3.2. Частица в одномерной потенциальной яме конечной глубины.. 11

4. Заключение. 17

5. Список используемой литературы.. 18

Введение

Квантовая механика — раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Поскольку постоянная Планка является чрезвычайно малой величиной по сравнению с действием повседневных объектов, квантовые эффекты в основном проявляются только в микроскопических масштабах. Если физическое действие системы намного больше постоянной Планка, квантовая механика органически переходит в классическую механику. В свою очередь, квантовая механика является нерелятивистским приближением (то есть приближением малых энергий по сравнению с энергией покоя массивных частиц системы) квантовой теории поля.

Классическая механика, хорошо описывающая системы макроскопических масштабов, не способна описать явления на уровне молекул, атомов, электронов и фотонов. Квантовая механика адекватно описывает основные свойства и поведение атомов, ионов, молекул, конденсированных сред, и других систем с электронно-ядерным строением. Квантовая механика также способна описывать поведение электронов, фотонов, а также других элементарных частиц, однако более точное релятивистски-инвариантное описание превращений элементарных частиц строится в рамках квантовой теории поля. Эксперименты подтверждают результаты, полученные с помощью квантовой механики.

Таким образом, квантовая механика является новым толчком, позволяющим открывать новые горизонты науки в целом. Данная работа направлена на раскрытие теоретических и практических аспектов одного из разделов квантовой механики.

2. Уравнение Шрёдингера

Основное уравнение квантовой механики является уравнение Шрёдингера, определяющее изменение состояния квантовых систем с течением времени. Относительно общего вида уравнения для 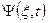можно лишь утверждать, что оно должно быть линейным и однородным (на основании принципа суперпозиции) и выражать первую производную 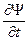волновой функции по времени через значение самой волновой функции в тот же момент времени 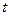. Последнее обстоятельство обусловлено тем, что волновая функция 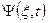полностью определяет состояние системы в момент времени 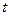, а, следовательно, и производную 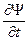в этот момент времени. В самом общем виде уравнение, удовлетворяющее указанным условиям, и носящем название временного уравнения Шрёдингера в конфигурационном пространстве, можно записать следующим образом:

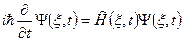, (1)

где 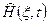— некоторый, подлежащий определению, линейный оператор, имеющий размерность энергии (учитывая введенный для удобства множитель 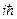в левой части уравнения (1)), также называемый оператор полной энергии или оператор Гамильтона (Гамильтонианом), которому соответствует следующая формула:

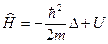. (2)

В микромире особая роль отводится системам со стационарным гамильтонианом, т. е. не зависящим от времени явно (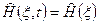), что соответствует, в частности, микрочастицам, движущимся в постоянных внешних полях, т. е гамильтониан не зависит от времени и совпадает с оператором полной энергии. В этом случае уравнение Шрёдингера

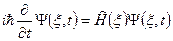(3)

имеет важные решения, получающиеся путем разделения переменных 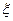и t:

. (4)

Подставляя (4) в (3) и обозначая постоянную разделения переменных через E, мы получаем:

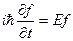, (5)

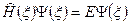. (6)

Первое уравнение решается сразу:

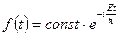. (7)

Что же касается второго уравнения, то, как видно, оно совпадает с уравнением для собственных функций оператора энергии 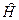. Если обозначить эти функции через , а собственные значения через 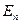(для определенности мы берем случаи дискретного спектра энергии), то окончательное решение (4) запишется в виде

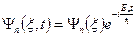, (8)

где функция 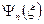должна удовлетворять уравнению

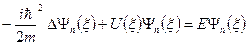, (9)

где 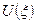— внешняя по отношению к частице потенциальная энергия в точке 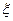; 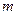— масса частицы; 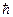— постоянная Дирака (редуцированная постоянная Планка), которая имеет вид

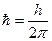, (10)

где 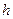— постоянная Планка.

Уравнение (9) получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для 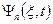(8).

Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

Выражение (8) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (8). Зависимость функции 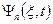от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (8) при одном выборе вида потенциальной функции 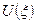совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (8) может быть решено аналитически лишь для небольшого числа частных типов функции .

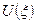Большое значение имеет интерпретация величины 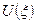в уравнении (8). Она производится следующим путём: временна́я зависимость функции 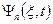в уравнении (8) имеет экспоненциальный характер, причём коэффициент при 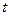в показателе экспоненты выбран так, что правая часть уравнения (9) содержит просто постоянный множитель 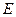. В левой же части уравнения(9) функция 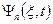умножается на потенциальную энергию 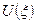. Следовательно, из соображений размерности вытекает, что величина 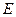должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что 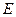представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера, 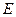действительно является полной энергией частицы при движении, описываемом функцией .

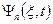Date: 2015-05-19; view: 385; Нарушение авторских прав