Собственные функции и собственные значения эрмитовых операторов. Случай дискретного и непрерывного спектра

Начнем с дискретного спектра, т.к. ему соответствует квадратично-интегрируемые функции. Задача на собственные функции и собственные значения для дискретного спектра:

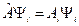(11.1)

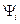-собственные функции

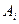- собственные значения

Так как 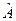эрмитов, то его собственные значения вещественны. Рассчитаем среднее 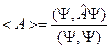. Если речь идет о физической величине, то 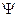это волновые функции, описывающие состояние системы. Если речь идет о математическом аппарате, то 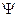- это любые функции. Как частный случай рассмотрим 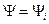, где 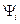- собственные функции оператора .

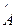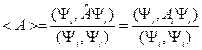
Так как 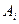- число, то его можно вынести за знак скалярного произведения, тогда:

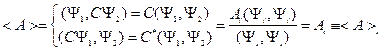
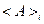- это среднее значение величины 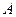в i -ом квантовом состоянии. Так как среднее – вещественно, то и собственные значения вещественны. У эрмитового оператора 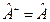собственные значения вещественны 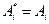(все эрмитовы операторы имеют вещественные спектры).

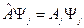(11.2)

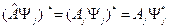
Умножая (11.1) скалярно на 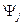слева, получим

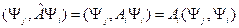(11.3)

Теперь (11.2) умножаем справа на 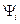, тогда

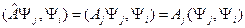(11.4)

Почленно из (11.3) вычтем (11.4):

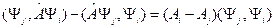(11.5)

т.к. 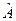- эрмитов (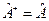), то 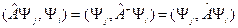. Из (11.5) имеем

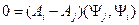(11.6)

Рассмотрим случай невырожденного спектра. Спектр вырожденный, если одному собственному значению соответствует несколько собственных функций. Например:

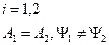
Невырожденный спектр – все собственные значения различные.

1) Рассмотрим (11.6) при 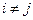, тогда , .

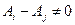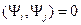2) Теперь пусть 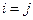. В этом случае скалярное произведение 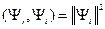. Обычно вводят нормировку .

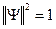Тогда случаи 1 и 2 дают условие ортонормированности:

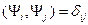
Утверждается, что собственные функции эрмитового оператора с дискретным спектром образуют полную систему функций, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Утверждение означает, что произвольную функцию можно разложить по собственным функциям эрмитового оператора как по базису.

Запишем это разложение:

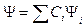, (11.7)

где индекс i пробегает по всем значениям, удовлетворяющим задаче (11.1).

Формулу (11.7) следует отличать от принципа суперпозиции

,

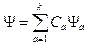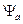где - вес состояния и суммирование ведется по произвольным a=1,…,k. Заметим, что если 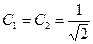(модель Юнга с ширмой и электроном), то .

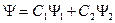Найдем коэффициенты 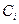из (11.7). Умножим скалярно (11.7) на 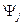, тогда имеем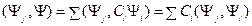

Применяя условие ортонормированности, получим:

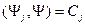
Тогда из (11.7) получаем

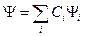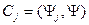, (11.7^/)

Далее

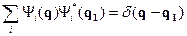
Из (11.7^/) также можно получить еще одно соотношение:

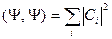- равенство Парсеваля (условие замкнутости).

Теперь рассмотрим случай непрерывного спектра.

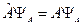
У собственной функции индексом является собственное значение. Собственные значения непрерывны, они сплошь заполняют соответствующую числовую ось. В этом случае собственные функции не нормируемы (квадратично не интегрируемы). Используем искусственную операцию – введем понятие собственных дифференциалов, по формуле:

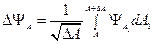
(11.8)

т. е. на числовой оси рассмотрим функции с равным весом на интервале 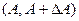. Собственные дифференциалы (11.8) квадратично-интегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций.

Условие ортонормируемости: .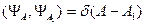

Здесь 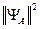дает расходящийся интеграл, т. е. равен 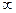. Но для собственных дифференциалов имеем:

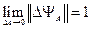
Собственные функции 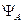обладают свойством полноты, т. е. они образуют базис, по которому может быть разложена любая функция:

,

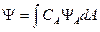По аналогии с дискретным спектром:

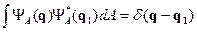
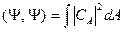- равенство Парсеваля

Date: 2015-05-19; view: 613; Нарушение авторских прав