Физический смысл квадрата модуля волновой функции Править

Волновая функция

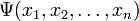
зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат еёмодуля

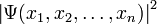
представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами

.

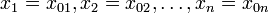Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.

Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.

Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциям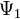и и 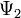, то она может пребывать и в состоянии, описываемом волновой функцией

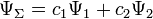
5) Неразрешимое противоречие этой модели заключалось в том, что электроны, чтобы не потерять устойчивость, должны двигаться вокруг ядра. В то же время они, согласно законам электродинамики, обязательно должны излучать электромагнитную энергию. Но в таком случае электроны очень быстро потеряли бы всю свою энергию и упали на ядро.

Следующее противоречие связано с тем, что спектр излучения электрона должен быть непрерывным, так как электрон, приближаясь к ядру, менял бы свою частоту. Опыт же показывает, что атомы излучают свет только определенных частот. Именно поэтому атомные спектры называют линейчатыми. Другими словами, планетарная модель атома Резерфорда оказалась несовместимой с электродинамикой Дж. К. Максвелла.

6) Докажем важное свойство ортогональности собственных функций квантовомеханических операторов. Есл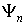и и 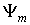- две собственные функции самосопряженного оператора 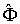, соответствующие различным собственным значениям и 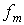, то они являются решениями следующих уравнений

.

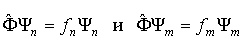(3.49)

.

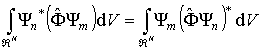(3.50)

Отсюда с учетом (3.49) получаем

.

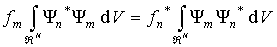(3.51)

Так как для самосопряженного оператора 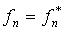, то (3.51) преобразуется к виду

.

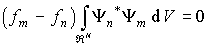(3.52)

Если 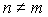, то 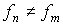, и из (3.52) получаем условие ортогональности собственных функций, соответствующих различным собственным значениям,

.

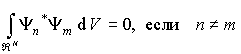(3.53)

Если волновые функци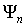и и 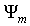считать нормированными на единицу, то условие ортогональности (3.53) собственных функций может быть записано как условие ортонормированности

,

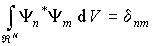(3.54)

где символ Кронекера 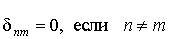, и .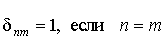

Date: 2015-05-19; view: 699; Нарушение авторских прав