Проверка статистических гипотез

Из принципа прак­тической достоверности, изложенного в предыдущем пунк­те, немедленно вытекает принцип практической невозмож­ности: события с очень малыми вероятностями можно в практических приложениях считать невозможными.

В качестве примера использования этого принципа на­помним правило трех сигм.

Вероятность того, что абсолютное отклонение нормально распределенной случайной величины превзойдет ее стан­дарт σ не более, чем в три раза, равна 0,9973. Значит, вероятность отклонения, большего 3 σ, равна 0,0027. С прак­тической точки зрения столь малой вероятностью можно пренебречь, что и приводит к правилу трех сигм.

Принципы практической достоверности и практической невозможности представляют собой, в сущности, одно и то же утверждение, примененное к противоположным событиям. Поэтому, вместо того чтобы говорить о практи­ческой достоверности некоторой доверительной оценки, можно говорить о практической невозможности отклонений, превышающих эту оценку. Если для нормально распределен­ной случайной величины в качестве доверительной вероят­ности взять 95%, то соответствующей доверительной оценкой абсолютного отклонения будет неравенство

Δξ ≤ 1,960.

Отклонения, большие чем 1,96 σ, нужно теперь считать прак­тически невозможными. Разумеется, такая оценка более «рискована», чем правило трех сигм, поэтому ею можно поль­зоваться лишь при малом числе предстоящих испытаний (чаще всего при одном испытании).

Допустим теперь, что отклонения Δξ, большие, чем не­которое доверительное число, признаны нами практически невозможными. Этот вывод был, очевидно, сделан на осно­вании некоторого теоретического распределения, которое, по тем или иным соображениям, мы считаем распределением величины ξ. Производя наблюдение, мы получим реальное значение отклонения Δξ. И может оказаться, что это реаль­ное значение превосходит доверительную оценку. Теперь сделаем из этого вывод.

Первое, что может прийти на ум — это влияние случая. Ведь доверительная оценка не является абсолютно досто­верной; возможно, здесь в первом же испытании сыграла роль та ничтожно малая (но существующая!) вероятность, которой мы пренебрегли в доверительной оценке. Однако при таком допущении пришлось бы отказаться от принци­па практической достоверности, который уже в тече­ние многих столетий надежно проверен человеческой практикой.

Поэтому более естественным будет второе предположе­ние: несоответствие принятого нами теоретического распре­деления реальному распределению величины ξ. Это несоот­ветствие может быть коренным (не тот тип распределения) или может быть связано с неправильным определением па­раметров распределения. Таким образом, принцип практи­ческой невозможности удается использовать в этом примере как один из критериев проверки гипотезы о распределении величины ξ.

Принцип практической невозможности может быть ис­пользован в самых различных задачах, где возникает необхо­димость проверять, случайно или неслучайно появилось то или иное событие. При этом всякий раз практическая не­возможность события полностью отвергает случайность его появления, заставляя пересмотреть исходные предпосылки вычисления вероятности.

Эти рассуждения ясно вырисовывают разницу исполь­зования теории вероятностей для изучения предстоящих или уже осуществившихся событий. По отношению к пред­стоящим событиям главное – это надежное предвидение, поэ­тому здесь мы интересуемся лишь событиями с большими вероятностями. Из осуществившихся же событий нас инте­ресуют в первую очередь события с малой вероятностью. Чем меньше расчетная вероятность уже осуществившегося события, тем больше его «неслучайность» и тем важнее эту «неслучайность» раскрыть. Событие как бы сильнее прико­вывает к себе внимание наблюдателя, становится для него более значимым.

Использование принципа практической невозможности для доказательства неслучайного появления события с ма­лой вероятностью называется принципом значимости. Наи­большее значение вероятности, несовместимой со случай­ностью события, называется уровнем значимости. Иными словами, уровень значимости есть максимум таких вероят­ностей, при которых события можно считать практически невозможными. Но событие, противоположное практически невозможному, является практически достоверным. Поэ­тому принятые нами уровень значимости и уровень досто­верности должны в сумме давать единицу.

Теперь можно дать более строгое определение значимо­сти событий. Событие А называется значимым, если его вероятность Р(А) меньше, чем принятый уровень значимо­сти. Чем выше уровень значимости, тем он «жестче», ибо тем большее число событий нельзя рассматривать как случай­ные. Уровень значимости — это как бы величина ячеек «сита», сквозь которое отсеиваются неслучайные события. Наи­более употребительны уровни значимости 0,05; 0,02; 0,01; реже 0,10 или 0,001. Чтобы лучше «почувствовать» уровень значимости, можно пользоваться аналогией между вероят­ностью и частотой, считая, что уровень значимости, выра­женный в процентах, показывает, сколько раз в ста испы­таниях мы рискуем ошибиться, объявив изучаемое событие неслучайным. Так, наиболее употребительный в данной книге 5%-ный уровень значимости допускает ошибку в пяти случаях из ста. Поскольку каждую проверку гипотезы мож­но считать одним испытанием, то такой уровень вполне до­пустим при единичных проверках.

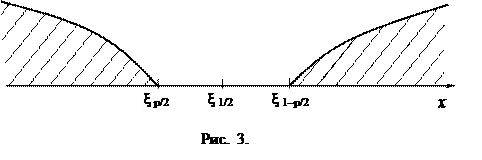Чаще всего принцип значимости применяется для про­верки так называемых статистических гипотез. Эти гипо­тезы имеют самые различные формулировки, но, в конеч­ном счете, являются гипотезами о распределении той или иной случайной величины. Проверка каждой такой гипо­тезы осуществляется следующим образом.

Выбирается уровень значимости р, ему соответствует доверительная вероятность 1 – р. По этой вероятности, используя гипотезу о распределении величины ξ, находят квантильные доверительные границы, как правило симметричные, т.е. ξ _р/2 и ξ _{1– р/2}. Числа ξ _р/2 и ξ _{1– р/2} называются кри­тическими значениями гипотезы; значения х, меньшие, чем ξ _р/2, и большие, чем ξ _{1– р/2}, образуют критическую область гипотезы (рис. 3). Для многих широко используемых на практике распределений составлены таблицы критических значений при различных уровнях значимости.

Следующим этапом находят реальное значение ξ _о изу­чаемой случайной величины (обычно его вычисляют по выборке). Если найденное значение ξ _о попадает в критическую область, то, по нашей гипотезе оно является практически невозможным. Но так как оно все-таки появилось, то долж­на быть отвергнута гипотеза. Если же ξ _о попадает между ξ _р/2 и ξ _{1– р/2}, то гипотеза вполне допускает такое значение в качестве случайного (на данном уровне значимости); поэтому нет никаких оснований ее отвергать.

Мы видим, что первое суждение (гипотеза неверна) гораздо более категорично, чем второе (гипотеза не отвер­гается, но и не утверждается, что она верна). И это не уди­вительно — в обоих случаях для проверки гипотезы используется лишь одно значение ξ _о. Но если для опровер­жения гипотезы достаточно одного противоречащего при­мера, то доказать правильность гипотезы нельзя даже с помощью тысячи подтверждающих примеров — опровер­гающим может оказаться еще не найденный нами тысяча первый. Конечно, и подтверждающие примеры не беспо­лезны для научного познания, ибо каждый такой пример есть испытание, увеличивающее вероятность того, что гипотеза правильна.

Принимая решение по результатам проверки, мы можем допустить ошибку. Возможные ошибки различаются по своему характеру. Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероят­ность такой ошибки не выше уровня значимости, следова­тельно, достаточно мала. Ошибка второго рода состоит в том, что гипотеза принимается, а на самом деле она не вер­на. Вероятность ошибки второго рода зависит от характера проверяемой гипотезы, от способа проверки и от многих других причин, что сильно усложняет ее оценку. Ясно только, что эта вероятность тем меньше, чем «жестче» при­нятый уровень значимости, ибо при этом увеличивается число отвергаемых гипотез.

Одну и ту же статистическую гипотезу можно исследо­вать с помощью различных случайных величин. Каж­дый такой способ исследования называется критерием значимости. Для проверки гипотезы стараются из всех возможных критериев выбрать тот, у которого при заданном уровне значимости меньше вероятность ошибки второго рода.