
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Доверительные интервалы и доверительные вероятности
|
|
Выше неоднократно отмечалось, что выборочные параметры могут служить приближенными оценками соответствующих генеральных параметров. При этом ограничивались простым утверждением, что погрешность такой оценки тем меньше, чем больше объем выборки. Теперь настало время выяснить, каким образом оценивается подобная погрешность.
Все выборочные параметры являются случайными величинами, следовательно, и их отклонения от генеральных параметров (погрешности) также будут случайными. Таким образом, вопрос об оценке этих отклонений носит вероятностный характер: а именно, можно лишь указать вероятность той или иной погрешности. Фактически мы решаем при этом задачу, в которой необходимо найти вероятность того, что некоторая случайная величина Δν (в нашем случае — отклонение выборочного параметра ν от исследуемого генерального) не превосходит по абсолютной величине некоторого заданного числа ε, Т. е. находится в пределах от – ε до ε. Эта задача легко решается, если известна функция распределения F(x) или плотность распределения f(x) величины Δν:
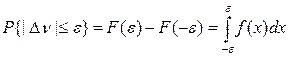 (2)
(2)
Распределение отклонения Δν есть смещенное распределение самого параметра ν. У этих распределений одинаковые дисперсии и все соответствующие моменты, различаются у них лишь математические ожидания. Иногда распределение Δν удается довольно точно (в пределах точности всех производимых вычислений) определить по элементам выборки, иногда это распределение вообще зависит только от объема выборки n и его можно вывести теоретически. Во всяком случае, знание этого распределения является обязательным условием для проведения соответствующего анализа.
Итак, допустим, что распределение Δν известно; в частности, известно M(Δν). Если бы при этом было известно математическое ожидание самого параметра ν, то величина l = Mν – M (Δν) дала бы точное значение генерального параметра. Однако Mν, как правило, неизвестно. Поэтому задачу о генеральном параметре решают следующим образом: находят из опыта (по выборке) одно значение ν o выборочного параметра ν и принимают его за приближенное значение генерального параметра l. Полученное выше неравенство (2) позволяет оценить это приближение.
Действительно, задаваясь некоторым положительным числом ε, мы можем найти вероятность Р того, что | Δν | = | ν — l | ≤ ε. Поскольку νo есть одно из допустимых значений случайной величины ν, то вероятность неравенства |ν o— l | = ε также равна Р.
Мы получаем формулу
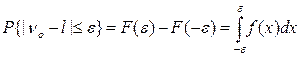 (3)
(3)
позволяющую сравнивать найденное значение выборочного параметра с неизвестным генеральным параметром.
Неравенство | ν — l | ≤ ε может быть переписано в виде νo — ε ≤ l ≤ νo + ε, что дает более наглядную оценку неизвестному генеральному параметру l; вероятность нового неравенства по-прежнему равна Р. Мы сталкиваемся здесь с неравенством иного типа, чем раньше, при изучении случайных величин, а именно, неизвестная (но не случайная) величина l оценивается случайными границами, ибо определенное по выборке значение νo является, вообще говоря, случайным. Подобная ситуация постоянно встречается в математической статистике, где для оценки любого параметра генеральной совокупности используются выборочные, а значит, случайные величины.
Итак, любая статистическая оценка есть оценка вида виде ν' ≤ l ≤ ν'', где ν' и ν'' – некоторые случайные величины. Придавая ν' и ν конкретные значения, мы сможем вычислять вероятность соответствующей оценки. Наиболее удобно в качестве границ ν' и ν'' брать квантили одной какой-либо случайной величины ν. Вероятность оценки ν p ≤ l ≤ ν q находится тогда очень легко и равна q – р.
Можно решать и обратную задачу: по заданной вероятности определить границы. Эта задача имеет бесчисленное множество решений — например, вероятности р соответствует любая оценка вида
 ν α ≤ l ≤ ν р+α ,
ν α ≤ l ≤ ν р+α ,
где 0 < α < 1 – р. При обработке наблюдений для оценок берут, как правило, симметричные квантили. В этом случае вероятности р соответствует оценка
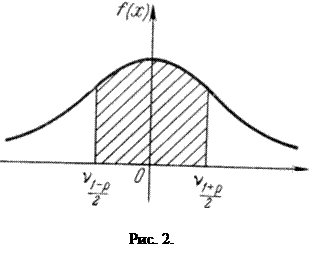
ν(1 – р)/2 ≤ l ≤ ν(1 + р)/2
Связь между квантильными границами и соответствующей вероятностью хорошо видна, если воспользоваться графиком плотности распределения величины ν (рис. 2). Квантили ν (1-p)/2 и ν (1+p)/2 находятся на одинаковом расстоянии от начала координат соответствующие им ординаты отсекают площадь, равную р (на рис. 2 заштрихована).
На практике это выглядит так, например, исследуя грунт, мы должны дать ответ, можно или нельзя здесь строить плотину; вряд ли строителей удовлетворит ответ: «Стройте с вероятностью 0,9». Более того, на основании наблюдений человечество сумело за всю историю науки сделать немало важных выводов, правильность которых подтверждена всем дальнейшим прогрессом. Хотя все эти выводы держатся лишь на случайных оценках!
И еще одно соображение: производя различные измерения, мы привыкли всегда указывать определенный, достоверный результат измерения. Если же мы и указываем погрешность, то это опять-таки вполне определенная, достоверная величина, причем небольшая, в то время как квантильные границы оценок могут быть сколь угодно большими.
Возникшее противоречие между теорией и практикой оказывается легко устранимым. Во всех перечисленных случаях результаты действительно являются достоверными. Однако при этом речь идет о так называемой практической достоверности, в отличие от абсолютной (или теоретической).
Событие называется абсолютно достоверным, если оно появляется при любом осуществлении комплекса основных факторов. Абсолютную достоверность нельзя установить никакой самой длительной проверкой, ее можно вывести лишь теоретически, путем логических умозаключений. Сюда относятся в основном математические истины и некоторые выводы других точных наук.
Большинство привычных достоверных событий при ближайшем рассмотрении не оказываются достоверными абсолютно. Нельзя, например, считать абсолютно достоверным тот факт, что подброшенная монета упадет или гербом, или цифрой — ведь у монеты есть и другие состояния равновесия (скажем, на ребре). Даже строго математически доказанные теоремы не всегда можно считать абсолютно достоверными, так как сюда примешивается возможность ошибки доказавшего теорему математика; могут ошибаться и те, кто проверял доказательство.
Таким образом, безупречное с научной точки зрения понятие абсолютной достоверности оказывается совершенно неприемлемым с практической точки зрения. Однако отбрасывать это понятие нельзя. Вероятность того, что событие А с вероятностью р осуществится во всех п испытаниях, равна рп. Но при р<1 (как бы ни было р близко к 1) обязательно рп →0 при n → ∞. А это значит, что проводя достаточно большое число испытаний, мы обязательно получим такое испытание, в котором событие А не произойдет. Если же вспомнить геометрическое определение вероятности, то мы столкнемся с событиями, вероятность которых даже равна 1 и которые, тем не менее, в отдельном испытании могут не произойти.
Итак, вопрос о том, какие результаты исследования можно считать практически достоверными, оказывается далеко не простым. Все в конечном счете зависит от того, сколь велико число дальнейших применений этого результата, а также сколь велика опасность единичной ошибки. Так, например, вероятность ясной погоды 0,9 достаточна для того, чтобы выйти из дому без зонтика; однако если 0,9 — это вероятность того, что у некоторого вещества не будет самопроизвольного взрыва, вряд ли вы станете небрежно хранить это вещество.
Из всего сказанного ясно, что событие А с вероятностью р ≈ 1 может считаться практически достоверным, если число п всех реально проводившихся ранее и проводимых в будущем испытаний над этим событием невелико, т. е. вероятность рп мало отличается от 1. Определение, как мы видим, весьма расплывчатое и к тому же несет в себе психологический элемент (оптимизм или скептицизм самого исследователя). Поэтому лучше всего регулярно указывать вероятность (уровень достоверности) каждого получаемого результата.
Отметим еще одно обстоятельство. Вероятность большинства реальных событий заранее неизвестна и вычисляется опять-таки с помощью испытаний. Поэтому каждое реально проведенное испытание, при котором появилось событие А, с одной стороны, Приближает то «роковое» испытание, в котором событие А может не появиться, а с другой стороны, увеличивает вероятность события А и, значит, отодвигает «роковое» испытание. Именно это обстоятельство и позволяет нам быть уверенными в появлении абстрактно не достоверных событий, осуществлявшихся уже в большом числе предыдущих испытаний.
Использование принципа практической достоверности позволяет не доводить окончательную вероятность оценки до 1 (что дало бы бесконечный интервал в качестве границ), а считать окончательной менее вероятную оценку. Принимаемый при этом уровень достоверности называется доверительной вероятностью. В зависимости от конкретных обстоятельств в качестве доверительной вероятности берут 0,95; 0,98; 0,99; реже 0,90 или 0,999.
Соответствующие доверительной вероятности квантильные границы называются доверительными границами, образуемый ими интервал — доверительным интервалом (или доверительной оценкой ).
Найдем, например, доверительную оценку генерального среднего а по одному наблюдению хо = 3, если известно, что генеральная совокупность имеет нормальное распределение со стандартом σ = 0,9. В качестве доверительной вероятности возьмем 0,95.
Как показано в начале пункта, соответствующая оценка имеет вид xo – ε ≤ l ≤ xo + ε, где ε есть оценка абсолютного отклонения. Иными словами, в качестве доверительных границ можно взять симметричные квантили υ0,025 и υ0,975 нормального распределения со средним хo = 3 и стандартом σ = 0,9. Используя формулу (1) предыдущего пункта, найдем, что
υ0,025 = 3 + 0,9 (—1,96) = 1,236,
υ0,975 = 3 + 0,9 *1,96) = 4,764
(здесь число и0,975 = l,96 найдено из таблицы). Окончательно получим, что
1,236 ≤ а ≤ 4,764.
Возможно, полученный доверительный интервал нас не устроит. Однако любое его сужение повлечет снижение доверительной вероятности, что нежелательно. Поэтому единственный путь улучшения оценок — снижение соответствующей дисперсии (путем улучшения методики, уточнения действующих факторов и т. д.).
Date: 2015-05-19; view: 1050; Нарушение авторских прав