Зонная теория твердых тел

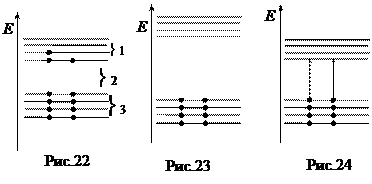Из рис. 21 видно, что в кристалле Na зона 3 S заполнена наполовину. Поэтому электроны могут переходить с одного уровня на другой в пределах этой зоны. Энергетическая схема металла представлена на рис. 22. По принципу Паули на каждом уровне может быть не более 2 электронов. Переход электронов в пределах зоны проводимости (1) с одного уровня на другой обеспечивает хорошую прово­димость металлов; (2) – запрещенная зона. У некоторых металлов заполненная зона (3) и зона проводимости перекрываются.

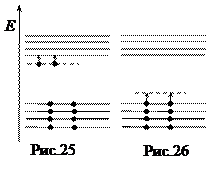
В диэлектриках (рис.23) ширина запрещенной зоны так вели­ка, что никаким воздействием нельзя перевести электроны в зону проводимости. Поэтому идеальный диэлектрик не проводит электрический ток. У полупроводника с собственной проводимостью (рис.24) ширина запрещенной зоны меньше. Под воздействием тепла или света электроны могут переходить в зону проводимости, создавая электронную проводимость (n -типа). При переходе электронов в зону проводимости в заполненной зоне остаются вакансии-дырки. Переход электронов в заполненной зоне на место образовавшихся вакансий можно рассматривать как движе­ние положительно заряженных дырок (проводимость р -типа). Таким образом, полупроводник с собственной проводимостью обладает двумя типами проводимости: п и р -типов. Проводи­мость одного типа можно получить в примесных полупровод­никах. На рис. 25 представлена энергетическая схема полу­проводника с проводимостью n -типа, а на рис. 26 – р -типа. В примесных полупроводниках с проводимостью п типа около зоны проводимости располагается энергетическая зона донорных примесей (пунктир). Электроны с донорных уровней переходят в зону проводимости даже при комнатной темпера­туре, обеспечивая проводимость п - типа. При этом дырки в заполненной зоне не образуются. В примесных полупровод­никах с проводимостью р - типа происходит переход электро­нов из заполненной зоны на акцепторные уровни примеси. При этом электроны в зоне проводимости не появляются.

Квантовые статистики изучают системы, состоящие из большого числа частиц. При описании столкнове­ния двух частиц говорят о вероятности их нахождения в области столкновения, ибо в квантовой механике нет понятия траектории. Это можно записать следующим образом: 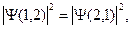где волновая функция системы зависит от координат обеих частиц. Последнее равенство может выполняться, ес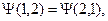ли или 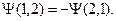В первом случае Y называют симметричной, во втором – антисимметричной. Иначе: волновая функция, системы из двух частиц либо симметрична, либо антисимметрична относительно перестановки этих частиц. Симметрия или антисимметрия волновой функции является свойством системы частиц одного сорта. В соответствии с этим частицы делятся на бозоны - частицы, описываемые симметричными волновыми функциями, и фермионы - частицы с антисимметричными волновыми функциями. Бозоны (фотоны, p - мезоны и т.д.) обладают целым спином. Фермионы (электроны, протоны, нейтроны) - полуцелым спином. Фермионы и бозоны совершено по-разному себя ведут. Например, число бозонов, находящихся на одном энергетическом уровне, может быть любым, в то время как для фермионов выполняется принцип Паули. Система бозонов подчиняется квантовой статистике Бозе-Эйнштейна, система фермионов – статистике Ферми-Дирака.

Статистика Ферми-Дирака. Уровень Ферми. Статистике Ферми-Дирака подчиняются частицы со спином 1/2. Для этих частиц справедлив принцип Паули – две частицы не могут находиться в одном и том же энергетическом состоянии. Рассмотрим металл при Т = 0 К. На рис. 27 изображена так называемая потенциальная яма для валентных электронов в металле, т.е. зона проводимости металла со вписанными в нее энергетическими уровнями. Электроны будут заполнять наиболее низкие энергетические уровни, верхний заполненный уровень называетсяуровнем Ферми при абсолютном нуле температур (рис. 27), где E_F (0) - энергия Ферми. Она специфична для каждого металла. На рис. 28 представлена функция распределения электронов по энергиям при Т= 0 К. Если температура металла отлична от 0 К, то электроны обнаруживаются и на уровнях выше E_F (0).

Функция распределения Ферми-Дирака имеет вид

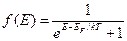. (91)

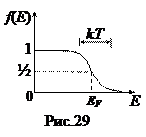Если Е = E_F, то f (E) = ½, т.е. при Т ¹ 0 уровень Ферми – это энергетический уровень, вероятность заполнения которого равна ½ (рис. 29). Вероятность заполнения уровней с Е > E_F, быстро уменьшается с ростом Е, т.к. изменения функции распределения происходят в узком энергетическом диапазоне (~ kT). Анализ формулы (91) показывает, что существует небольшая зависимость уровня Ферми от температуры.

В областях больших энергий Е–Е_F» kT единицей в знаменателе формулы можно пренебречь и получить

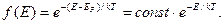(92)

Последняя формула представляет собой распределение Больцмана классической физики. В боль­шинстве полупроводников при комнатной температуре элек­тронный газ подчиняется классической статистике, в то время как в металлах пользоваться классической статистикой нельзя даже при температуре плавления. В полупроводниках с собственной проводимостью уровень Ферми располагается посередине запрещенной зоны, а в примесных полупроводниках несколько смещен к соответ­ствующим примесным уровням.

Работа выхода. Металл представляет для электронов проводимости потенциальную яму. Чтобы покинуть металл, электроны должны обладать энергией, достаточной для преодоления потенциального барьера на поверхности. Барьер обусловлен: а) тем, что случайное удаление электронов приводит к возник­новению в металле избыточного положительного заряда; б) наличием электронного облака у поверхности. В итоге образуется так называемый двойной слой, в котором на элек­троны действуют силы, направленные внутрь металла. Работа, совершаемая против этих сил, при удалении электрона из металла идет на увеличение потенциальной энергии электрона, т.е. потенциальная энергия электронов проводимости внутри металла меньше, чем вне металла на глубину ямы 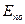. 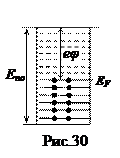Потенциальная энергия электрона связана с потенциалом той точки, где находится электрон, формулой 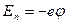, т.е. знаки Е_n и j противоположны. Следовательно, потенциал внутри металла больше, чем потенциал вблизи поверхности. Сообщение металлу положительного заряда приводят к увеличению потенциала как на поверхности, так и внутри металла, а следовательно, к уменьшению Е_n, а сообщение отрицательного заряда уменьшает j и увеличивает Е_n. Для удаления электрона из металла ему нужно сообщить различную энергию в зависимости от того, на каком уровне он находится. Наименьшая энергия для удаления из металла необходима электронам уровня Ферми (рис. 30). Эта энергия называется работой выхода. Она равна

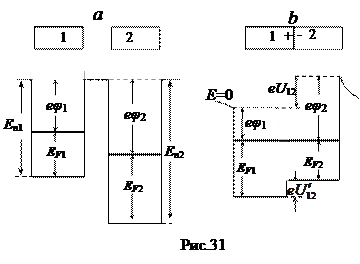
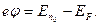
Контактная разность потенциалов. Термоэлектричество. Если два металла привести в соприкосновение, то при хорошем электрическом контакте между ними возникнет разность потенциалов, которую называют контактной. Рассмотрим графики потенциальной энергии двух металлов 1 и 2 до установления между ними контакта (рис. 31, а) и после (рис. 31, б). Пусть уровень Ферми в металле 1 лежит выше, чем в металле 2. Тогда при контакте электроны с верхних уровней 1 будут переходить на более низкие свободные уровни 2. При этом 1 зарядится положительно, а 2 – отрицательно, поэтому потенциальная энергия электронов в 1 уменьшается, а в 2 увеличивается. Условие равновесия при контакте - одинаковое положение уровней Ферми. При этом имеют место два скачка потенциала:

1 потенциальная энергия электронов вблизи 1 на 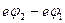меньше, чем вблизи 2. Следовательно, потенциал у 1 будет больше, чем у 2 на величину

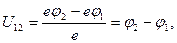
где U₁₂ - внешняя контактная разность потенциалов.

2 между внутренними точками возникает внутренняя контактная разность потенциалов

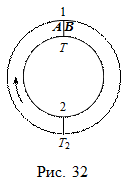
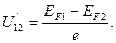
Наличие внутренней контактной разности потенциалов объясняет термоэлектрические явления. Рассмотрим цепь, состоящую из двух металлов А и В при наличии спаев 1 и 2 (рис. 32). Пусть температуры спаев различны: 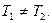Опыт показывает, что в такой системе возникает термоэлектродвижущая сила и протекает ток (эффект Зеебека). На явлении термоэлектричества основано измерение температуры термопарами, которые представляют собой спай двух металлов. Термопара константан-медь имеет эдс= 20 мВ при D Т = 500 К.

р-n переход возникает на границе двух полупроводников с различным типом проводимости вследствие диффузии носителей тока через контакт. В каждом полупроводнике с примесной проводимостью наряду с основными носителями, определяющими тип проводимости, имеется небольшое коли­чество неосновных носителей противоположного знака.

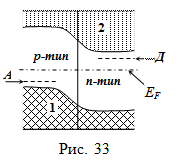
Энер­гетически схема двух полупроводников с различной проводи­мостью, находящихся в контакте, представлена на рис. 33. Как и в случае контакта металлов при контакте полупроводников (вертикальная линия) уровень Ферми располагается на одинаковой высоте. Изгибание границ, энергетических зон обусловлено различ­ными потенциалами областей с различной проводимостью в состоянии равновесия. Верхняя граница основной зоны (1) дает ход потенциальной энергии электронов, 2 – зона проводимости для электронов.

На рис. 34 представ­лена схема контакта двух полупро­водников с различными типами проводимости (рис.34, а), при подключении контакта в пропускном (рис.34, б) и запорном направлениях (рис.34, в). При контакте двух полупроводников в отсутствие внешнего напряжения ток основных носителей (I_ос) мал, так как трудно преодолеть потенциальный барьер, а ток неосновных носителей (I_неос), беспрепятственно проходящих через потенциальный барьер, мал так как их очень мало. При подключении напряжения, как показано на рис. 34, б, происходит уменьшение высоты потенциального барьера и его ширины. Это приводит к значительному увеличению тока основных носителей. Ток неосновных носителей по-прежнему мал из-за их малого количества. Такое подключение напряжения называется пропускным. Подключение напряжения (рис. 34, в) - запорное. При этом происходит увеличение высоты потенциального барьера и его ширины. Ток основных носителей становится даже меньше, чем без подключения напряжения. Полупроводниковые выпрямители, работа которых основана на односторонней проводимости р-n перехода, дают некоторый ток при отрицательных значениях напряжения, при больших обратных напряжениях происходит пробой, ток при этом возрастает.

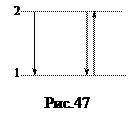ЛАЗЕРЫ

Вынужденное излучение. Рассмотрим два энергетических уровня в некоторой атомной системе (рис. 47). При переходе атома из одного энергетического состояния в другое поглощается или испускается квант излучения, величина которого

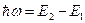. (93)

Поглощая энергию, атом переходит на более высокий энергетический уровень. Далее возможны два варианта возвращения атома в более низкое энергетическое состояние: самопроизвольное (это – спонтанный переход ), или спровоцированное встречей атома с фотоном, энергия которого равна разности (93). В последнем случае переход называется вынужденным, а фотон, испущенный атомом, оказывается в точности таким же, как и налетевший. В результате этого в одном направлении летят уже два одинаковых фотона.

Для отдельного атома вероятность вынужденного испускания из возбужденного состояния Е ₂ равна вероятности поглощения в нижнем состоянии Е ₁. Рассмотрим атомную систему, состоящую из большого числа возбужденных атомов. При термодинамическом равновесии количество атомов N_i, находящихся в состоянии с энергией Е_i, называется населенностью этого уровня энергии и определяется распределением Больцмана, в соответствии с которым населенность N_i экспоненциально убывает по мере роста i. Значит, N ₂ < N ₁ и вещество в целом поглощает электромагнитное излучение, несмотря на то, что для отдельного атома вероятность испускания фотона равна вероятности его поглощения. Действительно, вероятность поглощения фотона системой в целом пропорциональна N ₁, а вероятность испускания пропорциональна числу N ₂, которое меньше, чем N ₁, следовательно, поглощение преобладает. Поглощение может уступить место усилению электромагнитной волны при прохождении ее сквозь вещество, если удается создать условия, при которых N ₂ > N ₁. Такое неравновесное состояние вещества называется инверсной населенностью, а перевод системы в это состояние – накачкой. Появление в этой системе фотона с энергией (93) инициирует лавинообразное рождение вторичных фотонов, летящих в заданном первичным фотоном направлении. Получение такой лавины и является основной идеей лазерной генерации. Для возникновения как можно большего числа вторичных фотонов нужно, чтобы большая часть атомов вещества, называемого активной средой, находились в возбужденном состоянии (на рис. 47, в состоянии с энергией E ₂). Если в активной среде создана инверсная населенность, то любой фотон с энергией равной разности энергий Е ₂- Е ₁, вызывает лавинообразные переходы на нижележащий уровень, в ходе которых формируется лазерный луч. Направленность излучения и его усиление достигаются тем, что активная среда помещается между двумя зеркалами с общей оптической осью, одно из которых делается полупрозрачным. Такая система называется оптическим резонатором.

Впервые принцип усиления света за счет вынужденного излучения был предложен советским ученым Фабрикантом в 1940 г. Первые усилители, работающие в диапазоне сантиметровых волн (мазеры), были созданы в 1953 г. советскими физиками Басовым и Прохоровым и, независимо от них, американскими физиками Таунсом и Вебером.

Твердотельные лазеры. Рассмотрим энергетическую схему рубинового лазера. Рубин – это окись алюминия (Al₂O₃) с ионами хрома в качестве примеси. На рис. 48 представлены энергетические уровни ионов хрома, которые и являются рабочими для создания лазерного излучения. Генерация осуществляется по 3-х уровневой схеме. Кроме основного и возбужденного уровней в системе существует еще и промежуточный третий уровень – метастабильный, время жизни которого значительно больше (~10^-3 с), чем в возбужденном (~10^-8 с). В результате на метастабильном уровне накапливаются многие атомы, чем и создается инверсная населенность.

Для оптической накачки используется ксеноновая лампа-вспышка, работающая в импульсном режиме. При поглощении энергии лампы ионы Cr⁺⁺⁺ переходят в возбужденное состояние, время жизни в котором порядка 10^-8 с. Из этого состояния происходит переход на метастабильный уровень. При таком переходе часть энергии отдается кристаллической решетке. Инверсная заселенность создается за счет разницы времени жизни возбужденного и метастабильного уровней. Любой самопроизвольный переход с метастабильного уровня на основной (l =694,3 нм) вызывает лавинообразные переходы с такой же длиной волны.

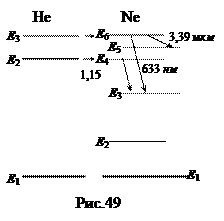Газовые лазеры. Большинство газовых лазеров работают по более сложной схеме, например, гелий-неоновый лазер (рис.49).

Date: 2015-05-19; view: 736; Нарушение авторских прав