
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Некоторые следствия соотношения неопределенностей
|
|
Закон Стефана-Больцмана устанавливает связь между энергетической светимостью и температурой тела: энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры
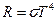 , (9)
, (9)
где s=5,67×10-8 Вт / м 2× К 4. Если (9) записать в виде 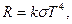 где 0 <k< 1, то, зная k, можно вычислять
где 0 <k< 1, то, зная k, можно вычислять 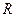 для тел, не являющихся абсолютно черными.
для тел, не являющихся абсолютно черными.
Спектральная плотность энергетическойсветимости (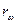 или
или 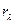 ) может быть введена не только для интервала частот (4), но и для интервала длин волн:
) может быть введена не только для интервала частот (4), но и для интервала длин волн:
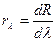 . (10)
. (10)
Закон смещения Вина: длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна абсолютной температуре тела
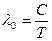 , (11)
, (11)
где С =2,9×10-3 м×К. На рис. 3 в соответствии с (11) l 02 >l 01, Þ Т 1 >Т 2. Площадь под кривой численно равна энергетической светимости абсолютно черного тела при соответствующей температуре.
Формулы Рэлея-Джинса и Планка. Чтобы найти вид функции 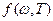 Рэлей и Джинс исходили из классической теоремы о равном распределении внутренней энергии по степеням свободы, где на каждое электромагнитное колебание приходится в среднем энергия kТ (по 0,5 kT на электрическую и магнитную энергию волны). Полученная формула
Рэлей и Джинс исходили из классической теоремы о равном распределении внутренней энергии по степеням свободы, где на каждое электромагнитное колебание приходится в среднем энергия kТ (по 0,5 kT на электрическую и магнитную энергию волны). Полученная формула
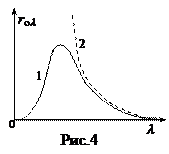
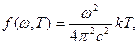 (12)
(12)
согласуется с опытом только при больших длинах волн (малых частотах). На рис. 4 представлены опытная зависимость r о l, (кривая 1) и кривая 2, полученная из формулы (12). Интегрирование формулы (12) в пределах от 0 до ¥ дает для энергетической светимости бесконечно большие значения, что иронично называется "ультрафиолетовой катастрофой". На самом деле при малых длинах волн не верна классическая формула (12). Чтобы получить согласующуюся с экспериментом формулу для f (w,Т) Планку пришлось ввести гипотезу, коренным образом противоречащую представлениям классической физики. В качестве модели Планк использовал полость с зеркальными стенками, внутри которой находятся осцилляторы, которые являются элементарными излучателями и поглотителями электромагнитного излучения. Планк допустил, что осциллятор обладает дискретным спектром значений энергии и может изменить свою энергию только на величину, кратную 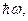 где
где  - постоянная Планка. В итоге была получена формула Планка
- постоянная Планка. В итоге была получена формула Планка
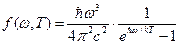 . (13)
. (13)
При малых w (больших l) эта формула переходит в формулу Рэлея-Джинса (12). Из формулы Планка можно получить экспериментальные законы Стефана-Больцмана (интегрированием формулы (13) в пределах от 0 до ¥) и смещения Вина (если выразить универсальную функцию Кирхгофа в виде 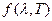 и решить задачу на нахождение экстремума). Гипотеза Планка о том, что электромагнитное излучение испускается и поглощается в виде квантов
и решить задачу на нахождение экстремума). Гипотеза Планка о том, что электромагнитное излучение испускается и поглощается в виде квантов 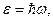 и вывод формулы (13) явились первым шагом в становлении квантовой физики.
и вывод формулы (13) явились первым шагом в становлении квантовой физики.
КВАНТОВАЯ ПРИРОДА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
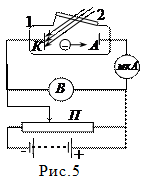 Фотоэффект. Законы фотоэффекта. Внешним фотоэффектом называется испускание электронов под действием электромагнитного излучения видимого и УФ -диапазона (рис. 5). Излучение попадает в откачанный баллон 1 через кварцевое окно 2. Напряжение между катодом (К) и анодом (А) регулируется с помощью потенциометра (П). Электроны, испускаемые фотокатодом, замыкают цепь, и микроамперметр фиксирует ток. Зависимость величины фототока I от напряжения U приведена на рис. 6. Начиная с некоторого напряжения U фототок достигает насыщения (Iн). С этого момента все электроны, испускаемые катодом, достигают анода. Интересно, что даже при малых отрицательных значениях U, не превышающих величину задерживающего потенциала U з, фототок отличен от 0. Следовательно, кинетическая энергия некоторых фотоэлектронов оказывается достаточной для того, чтобы электроны попадали на анод. Величину U з можно определить из условия:
Фотоэффект. Законы фотоэффекта. Внешним фотоэффектом называется испускание электронов под действием электромагнитного излучения видимого и УФ -диапазона (рис. 5). Излучение попадает в откачанный баллон 1 через кварцевое окно 2. Напряжение между катодом (К) и анодом (А) регулируется с помощью потенциометра (П). Электроны, испускаемые фотокатодом, замыкают цепь, и микроамперметр фиксирует ток. Зависимость величины фототока I от напряжения U приведена на рис. 6. Начиная с некоторого напряжения U фототок достигает насыщения (Iн). С этого момента все электроны, испускаемые катодом, достигают анода. Интересно, что даже при малых отрицательных значениях U, не превышающих величину задерживающего потенциала U з, фототок отличен от 0. Следовательно, кинетическая энергия некоторых фотоэлектронов оказывается достаточной для того, чтобы электроны попадали на анод. Величину U з можно определить из условия:
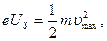
 где e - заряд, т - масса,
где e - заряд, т - масса, 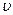 max - максимальная скорость фотоэлектрона. Максимальной скоростью обладают электроны, выбиваемые с поверхности металла. Опытным путем были установлены следующие законы фотоэффекта.
max - максимальная скорость фотоэлектрона. Максимальной скоростью обладают электроны, выбиваемые с поверхности металла. Опытным путем были установлены следующие законы фотоэффекта.
1. Фототок насыщения, возникающий при падении на фотокатод монохроматического потока излучения, пропорционален величине этого потока - закон Столетова
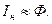
2. Максимальная скорость фотоэлектронов не зависит от величины потока, вызывающего фотоэффект, а определяется частотой падающего на фотокатод излучения
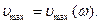
3. Для каждого металла существует некоторая минимальная частота wmin и соответственно максимальная длина волны lmax падающего излучения, при которых еще имеет место фотоэффект. Эту длину волны lmax называют красной границей фотоэффекта.
Уравнение Эйнштейна для фотоэффекта. Фотоны. На основании волновой теории максимальная скорость электронов должна определяться не частотой излучения, падающего на фотокатод, а величиной соответствующего потока. Развивая идеи М. Планка, А.Эйнштейн в 1905 г предпринял успешную попытку объяснения законов фотоэффекта. В соответствии с этой теорией энергия 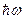 каждого кванта должна расходоваться на работу выхода электрона из металла (A) и сообщение фотоэлектрону кинетической энергии. Формула Эйнштейна для фотоэффекта имеет вид
каждого кванта должна расходоваться на работу выхода электрона из металла (A) и сообщение фотоэлектрону кинетической энергии. Формула Эйнштейна для фотоэффекта имеет вид
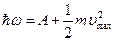 . (14)
. (14)
Из этой формулы следует выполнение второго и третьего законов фотоэффекта. Найдем выражение для красной границы фотоэффекта (для этого кинетическую энергию положим равной нулю). Минимальную энергию кванта, при которой еще возможен фотоэффект, определим из формулы (14):
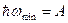 , Þ
, Þ 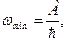 Þ
Þ 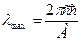 . (15)
. (15)
Квант (фотон) имеет скорость c =3×108 м/с, масса покоя его равна 0. Импульс фотона
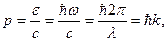 (16)
(16)
где k - волновое число. Фотон движется в направлении распространения электромагнитной волны.
Эффект Комптона состоит в том, что при рассеянии рентгеновских лучей с длиной волны l о, в рассеянном излучении присутствуют не только l о, но и большие длины волн l >l о. Согласно классической теории при рассеянии не должно быть изменения длин волн. Опыты Комптона показали, что эффект является результатом взаимодействия падающих на вещество рентгеновских фотонов со «свободными», т.е. слабее всего связанными электронами атомов. При этом смещение длины волны D l = l - l о зависит только от угла рассеяния q и не зависит от рассеивающего вещества. Законы сохранения энергии и импульса (рис. 7) для взаимодействия рентгеновского кванта со свободным электроном имеют вид
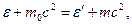 (17)
(17)
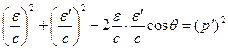 (18)
(18)
 где
где 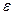 и
и 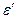 - энергии,
- энергии, 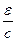 и
и 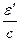 - импульсы падающего и рассеянного фотонов;
- импульсы падающего и рассеянного фотонов; 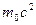 - энергия свободного электрона, масса которого ≈ массе покоя m 0;
- энергия свободного электрона, масса которого ≈ массе покоя m 0; 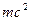 и
и 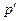 - энергия и импульс электрона после взаимодействия с фотоном. Связь между энергией и импульсом релятивистского электрона (см. инварианты теории относительности) имеет вид
- энергия и импульс электрона после взаимодействия с фотоном. Связь между энергией и импульсом релятивистского электрона (см. инварианты теории относительности) имеет вид
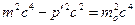 . (19)
. (19)
Из (17) найдем 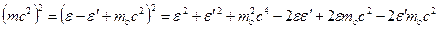 ; Из (18)
; Из (18)
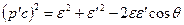 и подставим в (19). После сокращений получим
и подставим в (19). После сокращений получим
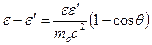 (20)
(20)
Переходя к длинам волн, получим величину сдвига длины волны в эффекте Комптона
 , или
, или 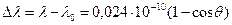 , м.
, м.
Величина D l весьма мала, и обнаружить ее можно только для рентгеновских лучей. Для видимого диапазона 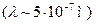 измерить столь малое изменение длины волныпрактически невозможно. Наличие несмещенной компоненты в рассеянном излучении обусловлено внутренними электронами атомов рассеивающего вещества. Такие электроны уже нельзя считать свободными. Их энергия связи сравнима с энергией рентгеновских фотонов. В этом случае обмен энергией и импульсом рентгеновского фотона происходит с атомом как целым. Поскольку масса атома значительно превышает массу электрона, комптоновское смещение фотонов на таких атомах ничтожно, и длина рассеянной волны совпадает с длиной волны падающего излучения.
измерить столь малое изменение длины волныпрактически невозможно. Наличие несмещенной компоненты в рассеянном излучении обусловлено внутренними электронами атомов рассеивающего вещества. Такие электроны уже нельзя считать свободными. Их энергия связи сравнима с энергией рентгеновских фотонов. В этом случае обмен энергией и импульсом рентгеновского фотона происходит с атомом как целым. Поскольку масса атома значительно превышает массу электрона, комптоновское смещение фотонов на таких атомах ничтожно, и длина рассеянной волны совпадает с длиной волны падающего излучения.
СТРОЕНИЕ АТОМА
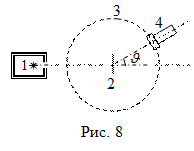
Модель атома Томсона. Опыты Резерфорда по рассеянию a-частиц. Одну из первых моделей атома, согласно которой положительный заряд равномерно распределен по всему объему атома, в который вкраплены электроны, предложил Томсон. Для проверки правильности этой модели в 1911-1913 гг. Резерфорд выполнил серию работ по рассеянию a -частиц (рис.8). Узкий пучок a -частиц от источника 1 падал на тонкую фольгу 2. На экране 3 в местах попадания a -частиц происходили вспышки, которые можно было наблюдать в микроскоп 4. Микроскоп можно было располагать под разными углами J. Вся установка находилась в откачанном объеме для предотвращения столкновений a -частиц с молекулами воздуха. Если справедлива модель Томсона (в атоме нет образований сравнимых по массе и величине заряда с a -частицей), то послепрохождения металлической фольги a -частицы не должны были менять свое направление. Действительно, почти все a -частицы не отклонялись от первоначального направления, однако некоторые регистрировались под углами J¹ 0, в том числе примерно 0,01 % частиц отклонялись на углы J > 90°. Следовательно, основная масса атома сконцентрирована в весьма малом (по сравнению с самим атомом) положительно заряженном ядре размером ~10-14 м (оценка Резерфорда), поэтому большинство a -частиц пролетает, не встречаясь с ядрами, и не меняет своего направления. По Резерфорду в центре атома находится положительно заряженное ядро, а вокруг ядра вращаются электроны. Однако в соответствии с классической электродинамикой, электрон, двигаясь с центростремительным ускорением вокруг ядра, должен излучать энергию и, в конце концов, упасть на ядро, т.е. атомы должны быть неустойчивыми системами, что противоречит опыту. Модель Резерфорда не могла разрешить это противоречие.
 Постулаты Бора. Датский физик Н.Бор в 1913 г. создал теорию атома, в основе которой лежат два постулата:
Постулаты Бора. Датский физик Н.Бор в 1913 г. создал теорию атома, в основе которой лежат два постулата:
1. Электроны в атомах могут находиться только на определенных стационарных орбитах, при этом не происхо дит ни излучения, ни поглощения энергии.
Условием стационарности орбит по Бору является квантование орбитального момента импульса электрона:
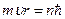 , где n = 1,2,3,…(21)
, где n = 1,2,3,…(21)
где m - масса электрона, 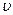 - его скорость, r - радиус орбиты.
- его скорость, r - радиус орбиты.
2. Излучение и поглощение энергии атомом происходит при переходе электрона с одной стационарной орбиты на другую. При этом величина кванта излучения или поглощения равна разности энергий соответствующих стационарных состояний:
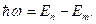
 (22)
(22)
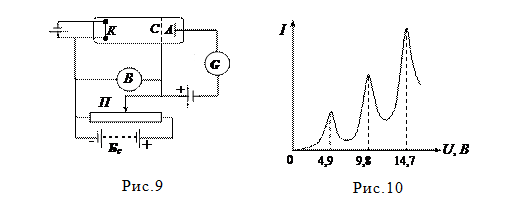 |
Первым доказательством существования дискретных энергетических уровней у атомов является опыт Франка и Герца (рис. 9). В трубке при пониженном давлении находятся пары ртути. Батарея Бс создает небольшое задерживающее поле (-0,5 В) между сеткой (С) и анодом (А). Ток регулируется потенциометром П. На рис. 10 представлена зависимость силы тока от напряжения между катодом и сеткой. Наличие максимумов объясняется следующим образом. При U =4,9 В энергия электронов равна 4,9 эВ. Пока энергия электронов меньше этой величины столкновения между ними и атомами ртути носят упругий характер, энергия электронов при этом не меняется, с ростом U растет I. При достижении электроном энергии 4,9 эВ и больше столкновения перестают быть упругими. Электроны отдают атомам ртути энергию 4,9 эВ. Оставшейся энергии может не хватить для достижения ими анода. Следовательно, разность между двумя дискретными уровнями атома ртути составляет 4,9 эВ. При энергии электронов 9,8 эВ они могут дважды не упруго столкнуться с атомами ртути и т.д.
Теория Бора атома водорода и водородоподобных ионов. Водородоподобными ионами называются ионы, имеющие один электрон, в частности, Не+, Li++, Ве+++.. При движении электрона по орбите имеет место второй закон Ньютона:
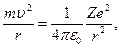 (23)
(23)
где е - заряд электрона, Zе - заряд ядра. Если (23) дополнить формулой (21) из первого постулата Бора, то можно определить радиус орбиты, скорость электрона на орбите, энергию электрона. Из (23) после сокращения на 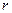 , следует
, следует
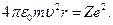 (24)
(24)
Поделим (24) на (21): 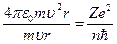 , Þ
, Þ 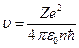 . (25)
. (25)
(25)®(23)® 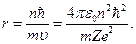 (26)
(26)
Полная энергия электрона на орбите складывается из кинетической и потенциальной энергии, причем потенциальная энергия отрицательна.
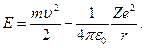 (27)
(27)
Из (23) следует 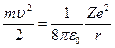 ® (27). Тогда полная энергия равна
® (27). Тогда полная энергия равна
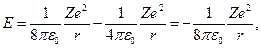 (28)
(28)
(26)®(28) ®
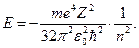 (29)
(29)
Таким образом, полная энергия электронов в стационарных состояниях является отрицательной. Для атома водорода  =1.
=1.
Закономерности в атомных спектрах. Недостатки теории Бора. Теория атома Бора позволила объяснить происхождение спектров атома водорода и водородоподобных ионов. Согласно Бору, частоты электромагнитных волн, излучаемых атомами, определяются разностью энергий стационарных состояний до и после излучения. К концу XIX было установлено, что атомные спектры состоят из отдельных линий, которые могут быть объединены в серии. Так, например, в спектре водорода фиксируется пять серий. В ультрафиолетовой области спектра наблюдается серия Лаймана, частоты линий которой подчиняются соотношению
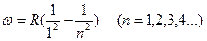 (30)
(30)
где R - постоянная Ридберга. Для серии Бальмера (видимая область спектра) выполняется соотношение 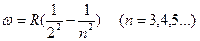 . (31)
. (31)
Для частот линий всех серий справедлива формула
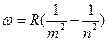 ,
, 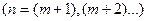 (32)
(32)
 При n ®¥, w ®
При n ®¥, w ® 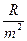 . Это значение частоты называется границей серии. Теория Бора хорошо объясняет приведенные выше закономерности. На рис. 11 представлены энергетические уровни атома водорода и переходы, соответствующие сериям Лаймана (a) и Бальмера (b) и Пашена (c). При больших значениях n уровни практически расположены непрерывно. Несмотря на успехи теории Бора, ей присущи и недостатки: 1) она не является ни последовательно классической, ни последовательно квантовой; 2) не объясняет устойчивости атома; 3) не позволяет создать теорию других атомов. Таким образом, теория Бора является только одним из этапов в создании более общей теории.
. Это значение частоты называется границей серии. Теория Бора хорошо объясняет приведенные выше закономерности. На рис. 11 представлены энергетические уровни атома водорода и переходы, соответствующие сериям Лаймана (a) и Бальмера (b) и Пашена (c). При больших значениях n уровни практически расположены непрерывно. Несмотря на успехи теории Бора, ей присущи и недостатки: 1) она не является ни последовательно классической, ни последовательно квантовой; 2) не объясняет устойчивости атома; 3) не позволяет создать теорию других атомов. Таким образом, теория Бора является только одним из этапов в создании более общей теории.
Гипотеза де Бройля. Вследствие двойственного характера электромагнитного излучения, особому микрообъекту фотону свойственен квантово-волновой дуализм: в одних опытах он проявляет квантовые (корпускулярные) свойства (фотоэффект, эффект Комптона), а в других - волновые (интерференция, дифракция). В 1924г. де Бройль предположил, что описанный выше дуализм присущ любым микрообъектам, например, электронам. Энергия и импульс фотона определяются формулами
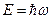 ; (33)
; (33)

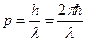 . (34)
. (34)
Гипотеза де Бройля заключалась в том, что любому движущемуся микрообъекту могут быть сопоставлены длина волны и частота, выраженные из формул (33) и (34), т.е.
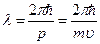 ;
; 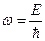 . (36)
. (36)
Например, для электрона, ускоренного в полях обычных электронных приборов (U ~1-104) B, скорость можно определить из формулы 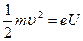 , Þ
, Þ
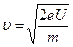 ® (36), Þ
® (36), Þ 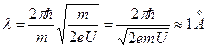 , (37)
, (37)
что ≈ длине волны рентгеновских лучей. Если размер приборов l~ 10 см, то l<<1, и волновые свойства пучка электронов в таких условиях не проявятся. Поэтому волновые свойства электронов стали искать на периодических структурах порядка межатомных расстояний, т.е. на кристаллических решетках. Так, в опыте Девиссона и Джермера (1927 г.) электроны отражались от поверхности монокристалла никеля (рис. 12) и затем попадали в цилиндр Фарадея (Ф), присоединенный к гальванометру. Большинство рассеянных электронов наблюдалось при угле j= 50о (и ускоряющем напряжении 54 В), указывающем на отражение от атомных плоскостей кристалла Ni, отстоящих друг от друга на расстояния  = 0,215 нм. Этот максимум можно истолковать, как максимум первого порядка от плоской дифракционной решетки с таким же периодом
= 0,215 нм. Этот максимум можно истолковать, как максимум первого порядка от плоской дифракционной решетки с таким же периодом 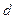 . Вычисление
. Вычисление 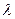 по формуле дифракционной решетки для первого максимума,
по формуле дифракционной решетки для первого максимума, 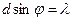 , дает величину
, дает величину 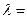 0,165 нм, а
0,165 нм, а
длина волны, вычисленная по формуле (37), оказалась равной 0,167 нм. Совпадение этих значений является прямым доказательством гипотезы де Бройля.
 Другим опытом, подтверждающим гипотезу де Бройля, являются опыты по дифракции электронов на поликристаллической структуре металлической фольги (Тартаковский, Томсон). Оказалось, что полученная таким образом дифракционная картина (рис.13), эквивалентна рентгенограмме, полученной при дифракции рентгеновских лучей на той же структуре. Поскольку через металлическую фольгу проходило одновременно большое количество электронов, можно было говорить о волновых свойствах пучка электронов. Однако в 1949 г. в СССР Биберман, Сушкин и Фабрикант провели опыты при последовательном прохождении отдельных электронов через фольгу. При достаточно большой экспозиции была получена весьма похожая дифракционная картина, чем было доказано, что отдельный электрон обладает волновыми свойствами. Таким образом, экспериментально была подтверждена гипотеза де Бройля.
Другим опытом, подтверждающим гипотезу де Бройля, являются опыты по дифракции электронов на поликристаллической структуре металлической фольги (Тартаковский, Томсон). Оказалось, что полученная таким образом дифракционная картина (рис.13), эквивалентна рентгенограмме, полученной при дифракции рентгеновских лучей на той же структуре. Поскольку через металлическую фольгу проходило одновременно большое количество электронов, можно было говорить о волновых свойствах пучка электронов. Однако в 1949 г. в СССР Биберман, Сушкин и Фабрикант провели опыты при последовательном прохождении отдельных электронов через фольгу. При достаточно большой экспозиции была получена весьма похожая дифракционная картина, чем было доказано, что отдельный электрон обладает волновыми свойствами. Таким образом, экспериментально была подтверждена гипотеза де Бройля.
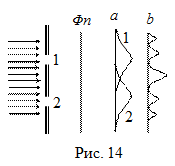
 Свойства микрообъектов. Микрообъект может проявлять как квантовые (корпускулярные), так и волновые свойства. Но, строго говоря, микрообъект не является в классическом представлении ни частицей, ни волной. Отличие микрообъекта от волны состоит, например, в том, что он всегда обнаруживается как целое, нельзя наблюдать пол-электрона. Волну же с помощью полупрозрачного зеркала можно разделить на части. Микрообъект отличается и от макрочастицы тем, что к нему в общем случае не применимо понятие траектории. Это поясняет эксперимент, в котором параллельный пучок электронов падает на ширму с двумя щелями (рис. 14). Эксперимент аналогичен опыту Юнга для волн. Сначала закроем щель 2. Почернение на фотопластинке Фп представлено кривой 1(а). Закрыв щель 1, получим кривую 2 (а). Если открыть обе щели, то результат почернения (б) - не является наложением кривых 1 и 2, но подобен картине при интерференции волн от двух когерентных источников. Интересно, что попытка экспериментально определить, через какую именно щель проходит электрон, разрушает интерференционную картину. Следовательно, на движение электрона каким-то образом оказывают влияние обе щели, что не совместимо с представлением о траектории движения электрона. Волны де Бройля отличаются от объективно существующих электромагнитных волн. Например, невозможно заранее указать место на фотопластинке, в которое попадет электрон. Это вносит в рассуждения вероятностный характер. Поэтому волны де Бройля называют волнами вероятности. Интенсивность сопоставляемой микрообъекту волны в некоторой точке оказывается пропорциональной вероятности найти частицу в окрестности той же точки.
Свойства микрообъектов. Микрообъект может проявлять как квантовые (корпускулярные), так и волновые свойства. Но, строго говоря, микрообъект не является в классическом представлении ни частицей, ни волной. Отличие микрообъекта от волны состоит, например, в том, что он всегда обнаруживается как целое, нельзя наблюдать пол-электрона. Волну же с помощью полупрозрачного зеркала можно разделить на части. Микрообъект отличается и от макрочастицы тем, что к нему в общем случае не применимо понятие траектории. Это поясняет эксперимент, в котором параллельный пучок электронов падает на ширму с двумя щелями (рис. 14). Эксперимент аналогичен опыту Юнга для волн. Сначала закроем щель 2. Почернение на фотопластинке Фп представлено кривой 1(а). Закрыв щель 1, получим кривую 2 (а). Если открыть обе щели, то результат почернения (б) - не является наложением кривых 1 и 2, но подобен картине при интерференции волн от двух когерентных источников. Интересно, что попытка экспериментально определить, через какую именно щель проходит электрон, разрушает интерференционную картину. Следовательно, на движение электрона каким-то образом оказывают влияние обе щели, что не совместимо с представлением о траектории движения электрона. Волны де Бройля отличаются от объективно существующих электромагнитных волн. Например, невозможно заранее указать место на фотопластинке, в которое попадет электрон. Это вносит в рассуждения вероятностный характер. Поэтому волны де Бройля называют волнами вероятности. Интенсивность сопоставляемой микрообъекту волны в некоторой точке оказывается пропорциональной вероятности найти частицу в окрестности той же точки.
Критерий классического описания. В каких случаях можно ограничиться классическим описанием, а когда микрообъект ведет себя принципиально квантовым образом? Обобщение экспериментальных фактов приводит к следующему критерию. Если в данной физической системе значение некоторой физической величины с размерностью момента импульса сравнимо с постоянной Планка  , то поведение этой системы может быть описано только в рамках квантовой теории. Если же значение указанной величины очень велико по сравнению с
, то поведение этой системы может быть описано только в рамках квантовой теории. Если же значение указанной величины очень велико по сравнению с  , то поведение системы с высокой точностью описывается законами классической физики.
, то поведение системы с высокой точностью описывается законами классической физики.
Соотношение неопределенностей. Особые свойства микрообъектов, выражают сформулированные в 1927 г. В.Гейзенбергом соотношения неопределенностей: невозможно одновременное и точное определение координаты и импульса (или скорости) микрообъекта. Это утверждение математически можно записать в виде неравенств:
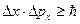 ;
;  ;
; 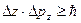 (38)
(38)
где D х, D y, D z - неопределенности в определении координат частицы; Dpx, Dpy, Dpz - неопределенности в определении соответствующихпроекций ее импульса.
Соотношение неопределенностей для энергии и времени записывается следующим образом:
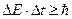 (39)
(39)
где D Е - неопределенность энергии микрообъекта, a D t - время существования в состоянии с этой энергией. Например, если атом находится в возбужденном состоянии, то D Е - естественная ширина энергетического уровня, соответствующего этому состоянию, а D t - время жизни атома в возбужденном состоянии. Неопределенности обусловлены не недостаточной точностью измерительных приборов, а сущностью самих микрообъектов.
 Покажем, что произведение неопределенностей имеет порядок величины постоянной Планка. Пусть микрообъект проходит через щель шириной D х (рис. 15), Þ неопределенность его координаты в момент прохождения щели равна D х. Оценим D рх, допустив, что частица на экране окажется в пределах первого дифракционного максимума (угол j определяет направление на первый минимум, Þ
Покажем, что произведение неопределенностей имеет порядок величины постоянной Планка. Пусть микрообъект проходит через щель шириной D х (рис. 15), Þ неопределенность его координаты в момент прохождения щели равна D х. Оценим D рх, допустив, что частица на экране окажется в пределах первого дифракционного максимума (угол j определяет направление на первый минимум, Þ 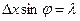 ). Тогда
). Тогда 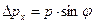 , Þ
, Þ 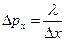 , Þ
, Þ
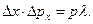 (40)
(40)
Подставляя длину волны де Бройля (36) → (40), получим 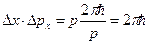 , что с точностью до порядка величины в правой части, совпадает с (38). Подставляя в (38) px=mux, получим
, что с точностью до порядка величины в правой части, совпадает с (38). Подставляя в (38) px=mux, получим 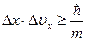 , Þ чем больше m, тем меньше неопределенность координаты и скорости. Поэтому для макрообъектов соотношения неопределенности учитывать не нужно.
, Þ чем больше m, тем меньше неопределенность координаты и скорости. Поэтому для макрообъектов соотношения неопределенности учитывать не нужно.
Некоторые следствия соотношения неопределенностей
1. К микрообъектам неприменимо понятие траектории. Это вытекает из того, что Dх¹ 0. Однако в некоторых случаях, например при движении электронов в электромагнитных полях в вакуумных устройствах (электронно-лучевая трубка), Dх мало и практически можно говорить о траектории электронов.
2. Доказательство стабильности атома (электрон не падает на ядро). Радиус атома водорода ~10-10 м, следовательно, для электрона в атоме водорода D x =10-10 м. Если бы электрон упал на ядро, размеры которого 10-14 м, то для него Dx=10-14 м. Учитывая, что  = 1,054·10-34 Дж·с, из (38) получим
= 1,054·10-34 Дж·с, из (38) получим
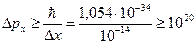 кг×м/с.
кг×м/с.
При этом импульс электрона должен иметь, по крайней мере, такой же порядок, а такому импульсу соответствует энергия электрона, при которой он должен вылететь из атома наружу.
Волновая функция. Развитием гипотезы де Бройля стало сопоставление движению микрообъекта волновой функции 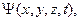 сделанное Шредингером. Свободное движение микрообъекта с определенной энергией и импульсом было предложено описывать волновой функцией, соответствующей плоской волне де Бройля. Эта функция имеет вид
сделанное Шредингером. Свободное движение микрообъекта с определенной энергией и импульсом было предложено описывать волновой функцией, соответствующей плоской волне де Бройля. Эта функция имеет вид
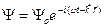 , (41)
, (41)
где 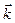 - волновой вектор (
- волновой вектор (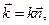
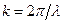 - волновое число,
- волновое число, 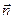 - нормаль к волновому фронту),
- нормаль к волновому фронту), 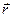 - радиус-вектор частицы. Поскольку микрообъекту свойственен корпускулярно-волновой дуализм, волновая функция не может иметь прямого физического смысла. Однако М. Борном была дана статистическая интерпретация
- радиус-вектор частицы. Поскольку микрообъекту свойственен корпускулярно-волновой дуализм, волновая функция не может иметь прямого физического смысла. Однако М. Борном была дана статистическая интерпретация 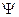 -функции, согласно которой квадрат ее модуля определяет вероятность (dP) того, что частица будет обнаружена в пределах некоторого объема dV.
-функции, согласно которой квадрат ее модуля определяет вероятность (dP) того, что частица будет обнаружена в пределах некоторого объема dV.
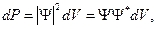 (42)
(42)
где Ψ* - комплексно сопряженная функция по отношению к Ψ; 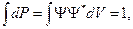 ибо этот интеграл определяет вероятность того, что микрообъект находится в одной из точек всего объема V, т.е. вероятность достоверного события. Условие, налагаемое на волновую функцию
ибо этот интеграл определяет вероятность того, что микрообъект находится в одной из точек всего объема V, т.е. вероятность достоверного события. Условие, налагаемое на волновую функцию
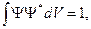 (43)
(43)
есть условие нормировки, а функция, удовлетворяющая этому условию, называется нормированной. Из (42) следует, что
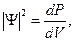 (44)
(44)
т.е. квадрат модуля волновой функции представляет собой плотность вероятности нахождения микрообъекта в соответствующем месте пространства.
Из смысла волновой функции следуют ее свойства: однозначность, конечность и непрерывность во всей области изменения, а также тот факт, по 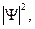 можно предсказать вероятность обнаружения микрообъекта в окрестности любой точки пространства.
можно предсказать вероятность обнаружения микрообъекта в окрестности любой точки пространства.
Принцип суперпозции состояний является одним из фундаментальных положений волновой теории. Из классической механики известно, что при суперпозиции волновых функций получается новая волновая функция. Кроме того, существует состояние покоя, в котором волновая функция равна нулю во всех точках пространства. В квантовой механике результат суперпозиции волновых функций будет существенно иным. Если, например, система может находиться в двух состояниях с энергиями Е1 и Е2, которые описываются волновыми функциями 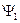 и
и 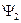 соответственно, то в результате суперпозиции этих состояний возможно состояние с волновой функцией
соответственно, то в результате суперпозиции этих состояний возможно состояние с волновой функцией
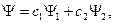 (45)
(45)
которая с вероятностью 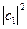 описывает состояние с энергией Е1 и с вероятностью
описывает состояние с энергией Е1 и с вероятностью 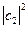 описывает состояние с энергией Е2. Набор всех
описывает состояние с энергией Е2. Набор всех 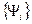 для любой физической величины (например, энергии) есть полная система собственных функций. Волновую функцию любого состояния можно разложить по собственным функциям:
для любой физической величины (например, энергии) есть полная система собственных функций. Волновую функцию любого состояния можно разложить по собственным функциям:
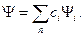 (46)
(46)
Уравнение Шредингера. В 1926 г. Шредингер написал основное уравнение для квантово-механического описания материи. Применение этого уравнения позволяет получить набор стационарных энергетических состояний в атомах, объяснить природу химической связи. Рассмотрим один из возможных путей получения уравнения Шредингера (это не вывод, поскольку уравнение Шредингера является основным постулатом квантовой физики). Параллельному пучку микрообъектов, движущихся вдоль оси X, в соответствии с (41) можно сопоставить волновую функцию
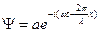 . (47)
. (47)
По де Бройлю свободному движению частиц соответствует плоская волна с частотой
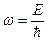 (48)
(48)
и длиной волны
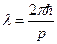 . (49)
. (49)
(48), (49) ®(47) ® 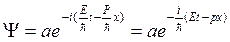 (50)
(50)
Найдем первую производную от этой функции по времени и вторую по координате
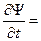
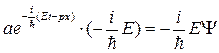 , Þ
, Þ 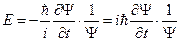 , (51)
, (51)
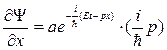 , Þ
, Þ 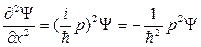 , Þ
, Þ
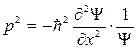 . (52)
. (52)
Подставим (51) и (52) в выражение 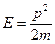 и получим уравнение Шредингера для свободной частицы, движущейся вдоль оси х:
и получим уравнение Шредингера для свободной частицы, движущейся вдоль оси х:
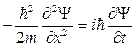 . (53)
. (53)
Если направление движения частиц не совпадает с осью х, то вместо (53) нужно написать
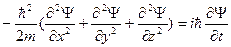 , или
, или 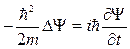 . (54)
. (54)
Это уравнение называется уравнением Шредингера для свободной частицы, т.е. частицы, не находящейся в потенциальном поле. В этом случае можно разделить временную и пространственную части волновой функции, т.е. представить ее в виде произведения
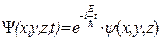 . (55)
. (55)
Подставляя (55) ® (54) получим 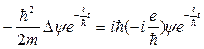 , что после сокращения приводится к виду
, что после сокращения приводится к виду 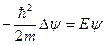 , или
, или 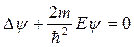 . (56)
. (56)
Уравнение (56) называется уравнением Шредингера для стационарных состояний свободной частицы. В общем случае стационарными состояниями называются состояния, для которых Е и | 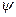 | не зависят от времени. При движении частицы в потенциальном поле
| не зависят от времени. При движении частицы в потенциальном поле
 (57)
(57)
где Е - полная энергия частицы, Ек - ее кинетическая энергия, U - ее потенциальная энергия. Для свободной частицы Е=Ек, следовательно, в общем случае
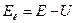 . ( 58 )
. ( 58 )
Подставляя Ек (58) ® (56) вместо Е, получим уравнение Шредингера для стационарных состояний частицы, движущейся в потенциальном поле
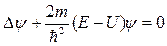 . (59)
. (59)
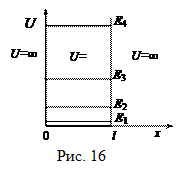 Частица в бесконечно глубокой одномерной потенциальной яме. Пусть частица может двигаться только вдоль оси х (рис. 16) и не может выйти за пределы ямы. При этом U = 0, если 0 £ х £ l и U = ¥, если х< 0 и х>l. Для одномерного случая из (59) получим
Частица в бесконечно глубокой одномерной потенциальной яме. Пусть частица может двигаться только вдоль оси х (рис. 16) и не может выйти за пределы ямы. При этом U = 0, если 0 £ х £ l и U = ¥, если х< 0 и х>l. Для одномерного случая из (59) получим
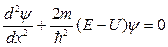 , (60)
, (60)
и для области внутри ямы
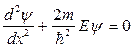 . (61)
. (61)
Обозначим 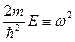 и подставим в (61):
и подставим в (61):
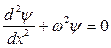 (62)
(62)
Это уравнение формально похоже на уравнение гармонических колебаний, только производная взята не по времени, а по координате. Поэтому решение уравнения (62) можно искать в виде
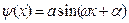 (63)
(63)
Отметим еще раз, что за пределами ямы частица оказаться не может. Поэтому вероятность обнаружить частицу вне ямы равна 0. Следовательно, из условия непрерывности волновой функции можно утверждать, что и на границах должны выполняться условия
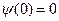 , (64)
, (64)
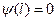 . (65)
. (65)
Рассмотрим совместно (64) и (65).
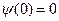 Þ
Þ 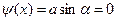 , Þ
, Þ 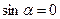 , Þ
, Þ 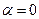 ; (66)
; (66)
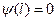 , Þ
, Þ 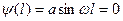 , Þ
, Þ 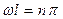 , где
, где 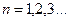 (67)
(67)
Взять n = 0 в формуле (67) нельзя, так как при этом волновая функция тождественно равна 0 и частица в яме отсутствует. Из (67) следует, что
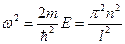 , Þ
, Þ 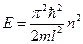 .
.
Таким образом, энергия частицы в бесконечно глубокой яме квантуется и собственные значения этой энергии зависят от целого числа 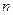 :
:

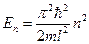 ,
, 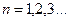 (68)
(68)
Разность энергий двух соседних уровней увеличивается с ростом 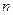 :
:
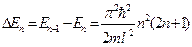 , (69)
, (69)
(см. рис. 21). Подставляя в (63) 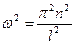 , получим собственные волновые функции
, получим собственные волновые функции
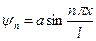 . (70)
. (70)
Величину а найдем из условия нормировки: 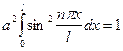 . В данном случае
. В данном случае

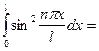
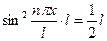 , где чертой отмечено среднее квадрата синуса, Þ
, где чертой отмечено среднее квадрата синуса, Þ 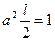 , Þ
, Þ
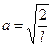 . (71)
. (71)
Подставляя (71)→ (70), получим нормированныесобственные волновые функции
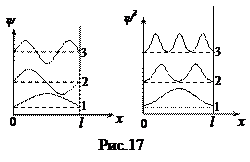
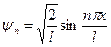 . (72)
. (72)
На рис. 17 представлены графики изменения волновой функции и квадрата ее модуля для первых трех значений n. Рассмотрим |ψ|2 для п= 2. Наибольшая вероятность обнаружить частицу имеем при x = l / 4 и x = 3 l / 4, однако при х = l/ 2 |ψ|2 = 0. Значит, в центре ямы и на её краях вероятность найти частицу близка к нулю (при n =2). Таким образом, частице в бесконечно глубокой яме нельзя приписать траекторию.
Квантовый гармонический осциллятор. В квантовой теории понятие силы теряет смысл, поэтому квантовый гармонический осциллятор определим как поведение микрообъекта массы 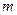 с потенциальной энергией
с потенциальной энергией 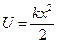 , такой же, как у классического осциллятора. Заметим, что график зависимости
, такой же, как у классического осциллятора. Заметим, что график зависимости 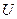 от х – парабола. Введем обозначение
от х – парабола. Введем обозначение 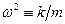 , тогда потенциальную энергию можно записать так
, тогда потенциальную энергию можно записать так
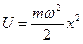 . (73)
. (73)
Запишем одномерное уравнение Шредингера для объекта с таким видом потенциальной энергии, т.е. уравнение Шредингера для квантового гармонического осциллятора
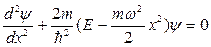 . (74)
. (74)
Мы не будем приводить решение этого уравнения из-за его сложности, однако отметим, что конечные, однозначные и непрерывные его решения могут иметь место только при собственных значениях энергии, равных
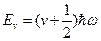 ,
, 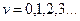 (75)
(75)
 Схема энергетических уровней квантового гармонического осциллятора представлена на рис.18. Видно, что уровни отстоят друг от друга на одинаковую величину. Минимальная энергия
Схема энергетических уровней квантового гармонического осциллятора представлена на рис.18. Видно, что уровни отстоят друг от друга на одинаковую величину. Минимальная энергия 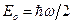 ¹ 0! То, что минимальная энергия квантового гармонического осциллятора не равна нулю (частица не может лежать на дне ямы) связано с принципом неопределенности. Если бы энергия равнялась нулю, то частица покоилась бы, и ее импульс и координата имели бы определенные значения, что противоречит принципу неопределенности. Детальный расчет показывает, что для квантового осциллятора допустимы лишь переходы между соседними стационарными уровнями энергии, при которых квантовое число v изменяется на единицу
¹ 0! То, что минимальная энергия квантового гармонического осциллятора не равна нулю (частица не может лежать на дне ямы) связано с принципом неопределенности. Если бы энергия равнялась нулю, то частица покоилась бы, и ее импульс и координата имели бы определенные значения, что противоречит принципу неопределенности. Детальный расчет показывает, что для квантового осциллятора допустимы лишь переходы между соседними стационарными уровнями энергии, при которых квантовое число v изменяется на единицу
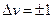 . (76)
. (76)
Это условие называется правилом отбора для квантового гармонического осциллятора.
 Колебания молекул. В атомной физике к осциллятору сводятся задача о колебаниях молекул и многие другие важные задачи. На рис. 19 представлена типичная потенциальная кривая взаимодействия атомов для двухатомной молекулы, где r – расстояние между атомами. Вид кривой U (r) показывает, что атомы могут совершать колебания относительно равновесного расстояния
Колебания молекул. В атомной физике к осциллятору сводятся задача о колебаниях молекул и многие другие важные задачи. На рис. 19 представлена типичная потенциальная кривая взаимодействия атомов для двухатомной молекулы, где r – расстояние между атомами. Вид кривой U (r) показывает, что атомы могут совершать колебания относительно равновесного расстояния 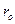 между ядрами атомов и у молекулы должны существовать дискретные уровни энергии. Эти уровни также описываются формулой (75), но теперь
между ядрами атомов и у молекулы должны существовать дискретные уровни энергии. Эти уровни также описываются формулой (75), но теперь 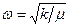 , где приведенная масса молекулы
, где приведенная масса молекулы 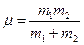 . Нижняя часть потенциальной кривой совпадает с параболой (пунктир), поэтому нижние уровни эквидистантны, как у квантового гармонического осциллятора. Поэтому весь колебательный спектр должен состоять из одной линии в соответствии с правилами отбора (76). На самом деле спектр является колебательно-вращательным. По мере увеличения амплитуды (и интенсивности) колебаний накапливается их отклонение от гармоничности: уровни сгущаются с ростом квантового числа v и в формулу (75) необходимо вводить поправку на ангармоничность. Спектры – незаменимый источник информации для структурных исследований в физике и химии, так как они исключительно чувствительны к особенностям строения молекул и межмолекулярным взаимодействиям.
. Нижняя часть потенциальной кривой совпадает с параболой (пунктир), поэтому нижние уровни эквидистантны, как у квантового гармонического осциллятора. Поэтому весь колебательный спектр должен состоять из одной линии в соответствии с правилами отбора (76). На самом деле спектр является колебательно-вращательным. По мере увеличения амплитуды (и интенсивности) колебаний накапливается их отклонение от гармоничности: уровни сгущаются с ростом квантового числа v и в формулу (75) необходимо вводить поправку на ангармоничность. Спектры – незаменимый источник информации для структурных исследований в физике и химии, так как они исключительно чувствительны к особенностям строения молекул и межмолекулярным взаимодействиям.
Атом водорода по Шредингеру. Атом водорода состоит из протона и электрона, где масса протона в 1836 раз больше массы электрона. Поэтому в первом приближении можно считать, что электрон движется в поле неподвижного протона. Уравнение Шредингера для электрона в атоме водорода имеет вид
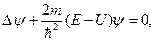 (77)
(77)
где потенциальная энергия электрона в поле протона равна 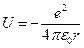 . (78)
. (78)
Так как U = U (r), а не от х, у, z, то и уравнение Шредингера нужно записать в сферических координатах. Связь между сферическими и прямоугольными координатами известна: 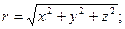
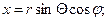
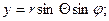
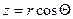 . Решение уравнения Шредингера в этом случае можно искать в виде
. Решение уравнения Шредингера в этом случае можно искать в виде 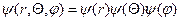 . Нормальное состояние атома водорода сферически симметрично, значит, волновая функция зависит только от r. В этом случае оператор Лапласа в сферических координатах записывается просто:
. Нормальное состояние атома водорода сферически симметрично, значит, волновая функция зависит только от r. В этом случае оператор Лапласа в сферических координатах записывается просто:
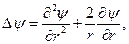 (79)
(79)
а само уравнение Шредингера после подстановки (79, 78) ®(77), выглядит так
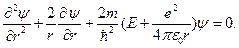 (80)
(80)
Сферически симметричную волновую функцию будем искать в виде
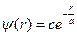 . (81)
. (81)
Отметим, что такая функция имеет конечное значение при r =0, а при r ®¥, 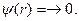 Находим первую и вторую производные (81) по r.
Находим первую и вторую производные (81) по r.

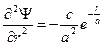 . (82)
. (82)
Подставим (81,82)®(80) Þ 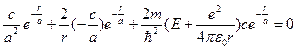 ; сокращаем и группируем:
; сокращаем и группируем:
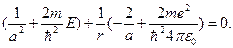
Это равенство должно выполняться при любых r, поэтому обе скобки должны в отдельности равняться нулю. Поэтому, решая систему, найдем величины а и Е:
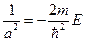
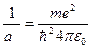
| 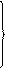
| Þ | 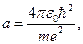
| (83) | |||
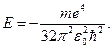
| (84) |
Сравнивая (83) и (84) с формулами (26) и (29), видим, что они эквиваленты радиусу первой боровской орбиты атома водорода и энергии электрона на ней, т.е. можно записать:
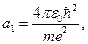
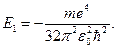 (85)
(85)
Вероятность нахождения электрона в шаровом слое радиуса r и толщиной dr, равна
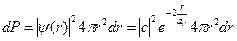 ,
,
где 4pr2dr – это объем шарового слоя радиуса r.
Следовательно, для рассматриваемого основного состояния атома водорода расстояния от электрона до протона распределены с плотностью вероятности
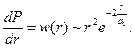
При этом если r = 0, то w(r) = 0 и если r®¥, то w(r) ®0. Таким образом, имеется определенная вероятность обнаружить электрон на любом расстоянии от ядра от 0 до ¥. Вычислим расстояние, на котором эта вероятность достигает максимума:
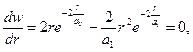
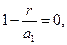 Þ
Þ 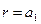 , (86)
, (86)
Следовательно, наибольшая вероятность соответствует расстоянию, равному радиусу первой боровской орбиты. Однако нужно иметь в виду, что в данном случае получилась сфера радиуса а1, а не плоская орбита по Бору. Существенно, что мы не получили при такой постановке задачи квантования энергии. Однако при допущении пребывания электрона только в области, ограниченной объемом атома, квантование автоматически получается из уравнения Шредингера (80). А именно: обнаруживается, что требованиям однозначности, конечности и непрерывности 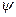 -функции можно удовлетворить при любых положительных значениях энергии, но в области отрицательных значений – только при дискретных значениях
-функции можно удовлетворить при любых положительных значениях энергии, но в области отрицательных значений – только при дискретных значениях
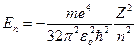 ,
, 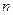 =1, 2, 3, …,
=1, 2, 3, …,
что совпадает с формулой (29) в теории Бора и эксперименту. Именно этот случай соответствует связанным состояниям электрона в атоме, причем вместо орбиты по Бору объект описывается вполне квантовой 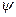 -функцией. Выяснилось также, что собственные функции
-функцией. Выяснилось также, что собственные функции 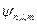 уравнения Шредингера (80) зависят от трех чисел, называемых квантовыми, которые описывают состояние электрона в атоме.
уравнения Шредингера (80) зависят от трех чисел, называемых квантовыми, которые описывают состояние электрона в атоме.
Квантовые числа. Состояние электрона в атоме водорода характеризуется тремя квантовыми числами: п, l, т.
п - главное квантовое число. Оно определяет дискретные значения энергии электрона в атоме. Для атома водорода
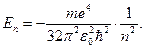 (87)
(87)
Это квантовое число может принимать следующие значения: n = 1, 2, 3,…
l - орбитальное квантовое число. Оно характеризует орбитальный момент импульса электрона:
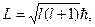 (88)
(88)
где l = 0,1,2,3,...(n -1). Из (88) следует, что орбитальный момент импульса электрона квантуется.
т - магнитное квантовое число - характеризует величину проекции 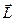 на направление внешнего магнитного поля:
на направление внешнего магнитного поля:
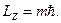 (89)
(89)
m имеет следующие значения: m = 0, ±1, ±2,...,± l.
 Пространственное квантование. Cледовательно, при данном значении l проекция орбитального момента импульса электрона на направление внешнего магнитного поля может принимать 2 l+ 1 значение, кратное
Пространственное квантование. Cледовательно, при данном значении l проекция орбитального момента импульса электрона на направление внешнего магнитного поля может принимать 2 l+ 1 значение, кратное  . Это связано с тем, что сам вектор
. Это связано с тем, что сам вектор 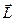 может иметь только определенную ориентацию в пространстве относительно направления внешнего магнитного поля
может иметь только определенную ориентацию в пространстве относительно направления внешнего магнитного поля 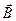 . Этот факт называется пространственным квантованием. На рис. 20 представлены возможные ориентации вектора
. Этот факт называется пространственным квантованием. На рис. 20 представлены возможные ориентации вектора 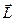 относительно направления внешнего магнитного поля.
относительно направления внешнего магнитного поля.
В 1925 г. Гоудсмит и Уленбек предположили, что наряду с орбитальным моментом импульса электрона существует собственный момент импульса электрона - спин и связанный с ним собственный магнитный момент. Электрон можно рассматривать как частицу, вращающуюся вокруг собственной оси. При таком вращении возникает собственный момент импульса. Можно ввести четвертое квантовое число ( спиновое) – тS, которое характеризует проекцию собственного момента импульса электрона на направление внешнего магнитного поля.

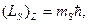 (90)
(90)
где LS - собственный момент импульса электрона. Квантовое число mS может принимать только два значения mS = ±1/2. В 1921 Штерн и Герлах опытным путем обнаружили пространственное квантование. Опыты ставились для определения магнитных моментов атомов первой группы таблицы Менделеева.
|
Принцип Паули: в атомной системе не может быть двух электронов с одинаковым набором четырех квантовых чисел. Найдем, исходя из этого принципа, количество электронов, находящихся в состоянии при данном значении главного квантового числа п. Так как магнитное квантовое число имеет 2 l+ 1 значение, спиновое - 2 значения, а орбитальное квантовое число меняется от 0 до п- 1, то искомое количество электронов равно
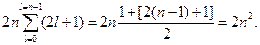
Из принципа Паули следует, что на одной атомной орбитали с соответствующими n, l и m могут находиться максимум два электрона с ms = + ½ и ms = - ½.
Многоэлектронные атомы. Чтобы построить многоэлектронный атом, нужно мысленно последовательно заселить все электронные орбитали, начиная с наиболее близких к ядру.
Введем некоторые обозначения, которые помогут компактно записывать электронные состояния. Электроны с различными значениями l обозначаются следующим образом:
l = 0, 1, 2, 3 ...
s p d f …
Комбинация главного квантового числа с буквой, характеризующей орбитальный момент импульса электрона, позволяет записывать состояния электронов. Например, 2 s (n= 2, l= 0); 4 d (n=4, l= 2). Электроны атома, имеющие одинаковое главное квантовое число, образуют слои: п = 1 – К-слой, п = 2 – L-слой, n = 3 – М-cлой, п = 4 – N-слой и т.д.
Отметим, что у многоэлектронных атомов в отсутствие внешнего магнитного поля энергия электронов зависит только от квантовых чисел n и l и не зависит от m.
В 1869 г. Д.И. Менделеев открыл периодический закон изменения химических и физических свойств элементов в зависимости от их порядкового номера, который определяется числом электронов в атоме. Проведем заполнение электронных состояний некоторых атомов в соответствии с принципом Паули (таблица).
Из таблицы видно, что сходство свойств элементов определяется характером заполнения электронных оболочек. Например, свойства интертных газов Не, Ne, Кr или щелочных металлов Li, Na, К.
| Номер | Элемент | К-слой | L | M | N | ||||||
| элемента | S-эл-ны | s | p | s | p | d | s | p | d | f | |
| H He Li Be B Ne | |||||||||||
| Na Mg Ar | |||||||||||
| K Ca Sc Kr |
Из таблицы также следует, что в некоторых случаях энергетически более выгодным оказывается заполнение последующих слоев при не полностью заполненных предыдущих (K, Ca), т.е. нарушается идеализированная схема заполнения орбиталей в соответствии с последовательно увеличивающейся энергией электронов. В дальнейшем это явление удалось объяснить теоретически включением в рассмотрение взаимодействия электронов между собой и с полем ядра. Отметим, что квантовая механика дала теоретическое объяснение открытию Д.И. Менделеева.
Date: 2015-05-19; view: 629; Нарушение авторских прав