Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Узлы стоячей волны
|
|
Стоячие волны
Волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Уравнение стоячей волны
Складываем волны
и 
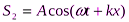
S=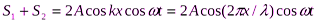 
(учли, что k = 2π/λ)— уравнение стоячей волны.
Пучности стоячей волны
Точки, в которых амплитуда максимальна (Aст = 2Аcos(2πx/λ)). Это точки среды, для которых
2πx/λ=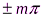 
(m=0,1,2,….)
Координаты пучностей
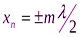(m = 0,1, 2,:..).
Узлы стоячей волны
Точки, в которых амплитуда колебаний равна нулю (Aст = 0). Это точки среды, для которых
(m = 0,1, 2,:..).
Координаты узлов
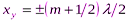(m = 0,1, 2,...).
Расстояния пучность—пучность и узел—узел равны λ/2, а расстояние пучность—узел равно λ /4.
Образование стоячих волн наблюдают при
интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность, если более плотная — узел. Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если волна отражается от менее плотной среды, то изменения фазы не происходит, и у границы колебания складываются с одинаковыми фазами — получается пучность.
Уравнение стоячей волны и его анализ
Частным случаем интерференции волн, являются стоячие волны.
Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию.
Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приводится в колебательное движение.
При наложении двух когерентных бегущих плоских волн вида
и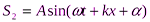 
где α-разность фаз волн в точках плоскости x=0, образуется плоская синусоидальная стоячая волна, описываемая уравнением
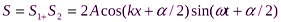
Амплитуда стоячей волны в отличие от амплитуды бегущих волн является периодической функцией координаты x.
Аст.=2А[cos*(k*x+α/2)]
Точки,в которых амплитуда стоячей волны равна 0, называются узлами, а точки где амплитуда двойная –пучности.
Положение узлов и пучностей находится из условий
k*x+α/2=(2m+1)π/2 (узлы)
k*x+α/2=m*n (пучности),где m=0,1,2…
Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн.
В бегущей волне фаза колебаний зависит от координаты x рассматриваемой точки. В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), так как аргумент синуса в уравнении стоячей волны не зависит от координаты x. При переходе через узел фаза колебаний изменяется скачком на π,так как при этом cos(k*x+α/2) изменяет свой знак на противоположный.
| <== предыдущая | | | следующая ==> |
| Испытание и наладка тепловых сетей | | | Мышление богатых |
Date: 2015-05-19; view: 15978; Нарушение авторских прав