Практическое задание к вопросу № 2. Умозаключения

Вопросы для самостоятельного изучения

по разделу «Элементы математической логики»

Вопрос № 1. Теоремы.

1.1. Понятие «теорема». Структура теоремы.

1.2. Виды теорем.

Вопрос № 2. Умозаключения.

1.3. Умозаключения и сопутствующие понятия.

1.4. Дедуктивное умозаключение.

1.5. Недедуктивное умозаключение.

а) неполная индукция

б) аналогия

+

Практическое задание (см. стр. 3).

Вопрос № 3. Доказательство.

1.1. Понятие доказательства.

1.2. Структура доказательства.

1.3. Виды доказательства.

1.4. Методы доказательства.

+

Практическое задание (см. стр. 4).

Вопрос № 4. Математические понятия. Определения понятий.

1.1. Объем и содержание понятия. Закон обратного отношения между объемом и содержанием понятия.

1.2. Отношения между понятиями.

1.3. Определение понятий.

Комментарии к вопросам для самостоятельного изучения

1) Каждый разобранный вопрос для самостоятельного изучения приносит в рейтинг студента 1 балл (по разделу «Элементы математической логики» всего 4 балла)

2) Теоретические вопросы должны быть законспектированы в тетради для лекций.

3) Сообщение по каждому подвопросу приносит 2 балла (2-3 минуты). Сообщение должно быть представлено в электронном и печатном виде (прислать предварительно на эл. адрес [email protected] - шрифт Times New Roman, 14 кегль, абзацный отступ 1 см, межстрочный интервал одинарный; наличие правильно оформленного титульного листа)

4) Практическое задание по вопросу приносит в рейтинг максимум 5 баллов (условия задач + решение в отдельной тетради в клетку)

Практическое задание к вопросу № 2. Умозаключения.

1. Даны утверждения: А(х): «Число х чётное», В(х): «Запись числа х оканчивается цифрой 4». Находятся ли они в отношении следования?

2. Запись числа оканчивается цифрой 8. Следует ли из этого, что данное число делится а) на 2; б) на 4?

3. В четырёхугольнике ABCD диагонали равны и в точке пересечения делятся пополам. Верно ли, что ABCD: а) ромб; б) квадрат; в) прямоугольник?

4. В четырёхугольнике ABCD все стороны равны. Достаточно ли этого для того, чтобы утверждать, что ABCD: а) квадрат; б) ромб?

5. В четырёхугольнике ABCD два угла прямые. Достаточно ли этого для того, чтобы утверждать, что ABCD – прямоугольник?

6. Выделите посылки и заключение:

1) Если число натуральное, то оно целое; если число целое, то оно рациональное. Следовательно, если число натуральное, то оно рациональное.

2) Если число натуральное, то оно целое; число 138 – натуральное. Следовательно, оно целое.

3) Всякое натуральное число целое; число 138 – целое. Следовательно, оно натуральное.

4) Всякое натуральное число целое; число 0,2 не является целым. Следовательно, оно не является и натуральным.

5) Если треугольник равнобедренный, то углы при основании равны; треугольник АВС – равнобедренный. Следовательно, углы при основании у него равны.

6) Во всяком равнобедренном треугольнике углы при основании равны; углы при основании треугольника АВС не равны. Следовательно, треугольник АВС не является равнобедренным.

7) Во всяком равнобедренном треугольнике углы при основании равны; треугольник АВС – не равнобедренный. Следовательно, углы при основании не равны.

7. Проанализируйте схему каждого умозаключения из упр. 6. Есть ли среди них умозаключения, не являющиеся дедуктивными?

8. Даны начала умозаключений:

1) Если четырёхугольник – прямоугольник, то в нём диагонали равны. Четырёхугольник ABCD – …

2) Равные треугольники имеют равные площади. Треугольники АВС и KLM …

3) Для того, чтобы ромб был квадратом, достаточно. Чтобы в нём был прямой угол. Ромб ABCD …

Закончите умозаключения так, чтобы они были дедуктивными, используя правило

а) заключения б) отрицания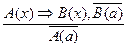

9. Используя круги Эйлера, проверьте, правильны ли умозаключения:

1) Всякий квадрат является прямоугольником; четырёхугольник ABCD не квадрат. Следовательно, он не является прямоугольником.

2) Некоторые прямоугольники – квадраты; все квадраты – правильные многоугольники. Следовательно, некоторые прямоугольники являются правильными многоугольниками.