Столкновения частиц. Диаграммы импульсов

Зіткнення частинок.

Діаграма імпульсів.

Підготувала студентка

2-го курсу магістратури

кафедри молекулярна фізика

Лаврик Юлія Михайлівна

Столкновения частиц. Диаграммы импульсов.

Будем считать:

1) исходная K -система отсчета инерциальная,

2) система из двух частиц замкнутая,

3) импульсы (и скорости) частиц до и после столкновения соответствуют достаточно большим расстояниям между ними; при этом потенциальной энергией взаимодействия можно просто пренебречь.

Величины, относящиеся к системе после столкновения, будем отмечать "крышечкой" сверху (например 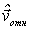- вектор относительной скорости после столкновения), а величины в С -сиcтеме штрихом.

Выделяют три вида столкновения частиц: абсолютно неупругое, абсолютно упругое и промежуточный случай - неупругое.

В результате абсолютно неупругого столкновения обе частицы "слипаются" и далее движутся как единое целое. Пусть две частицы, массы которых 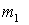и 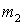имеют в K -системе до столкновения скорости и 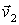. После столкновения образуется частица с массой 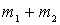, что прямо следует из аддитивности массы в ньютоновой механике. Скорость 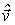образовавшейся частицы можно найти сразу из закона сохранения импульса:

.

Ясно, что скорость 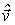равна скорости центра масс системы.

В С -системе этот процесс выглядит наиболее просто: до столкновения обе частицы движутся навстречу друг другу с одинаковыми значениями импульсов 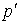, а после столкновения образовавшаяся частица оказывается неподвижной. При этом суммарная кинетическая энергия 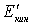частиц целиком переходит во внутреннюю энергию 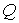образовавшейся частицы, то есть 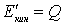. Отсюда найдем

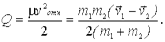
Таким образом, величина 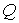для данной пары частиц зависит только от их относительной скорости.

В результате абсолютно упругого столкновения внутренняя энергия частиц не меняется, а поэтому не меняется и кинетическая энергия системы. Рассмотрим два частных случая: центральное и нецентральное упругие столкновения.

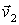1. При центральном столкновении обе частицы до и после столкновения движутся по одной и той же прямой, так как у обеих частиц скорости направлены вдоль прямой, соединяющей их центры масс. Пусть до столкновения скорости частиц в K -системе отсчета равны и (частицы движутся или навстречу друг другу, или одна частица догоняет другую). Определим скорости этих частиц после столкновения.

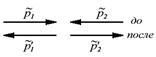
Столкновение частиц в системе центра масс

Рассмотрим этот процесс в С -системе, где до и после столкновения обе частицы имеют одинаковые по модулю и противоположные по направлению импульсы. Более того, так как суммарная кинетическая энергия частиц до и после столкновения одинакова, также как и их приведенная масса, то, импульс каждой частицы в результате столкновения изменит только направление на противоположное, не меняясь при этом по модулю, т. e 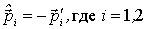. Аналогично, и скорости каждой частицы в С -системе будут противоположны:

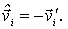
2. Нецентральное столкновение возникает, когда при столкновении скорость хотя бы одной из частиц не лежит на прямой, соединяющей их центры масс. Ограничимся случаем, когда одна из частиц покоится до столкновения. Пусть в K -системе отсчета частица массы 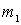с импульсом p испытала упругое нецентральное столкновение с покоившейся частицей массы 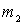. Рассмотрим этот процесс также сначала в С -системе. Здесь, как и в предыдущем случае, обе частицы в любой момент времени до и после столкновения имеют одинаковые по модулю и противоположные по направлению импульсы. Кроме того, импульс каждой частицы изменится по модулю в результате столкновения, т. е.

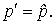
Однако направление разлета частиц теперь будет иным. Оно будет составлять с первоначальным направлением движения некоторый угол 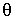, зависящий от закона взаимодействия частиц и их взаимного расположения в процессе столкновения.

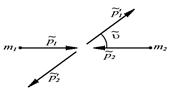
Нецентральный удар частиц

Теперь найдем импульс каждой частицы в K -системе отсчета после столкновения. С помощью формул преобразования скоростей при переходе от С к K -системе получим:

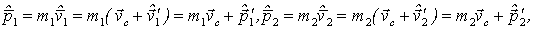
(4.20)

где 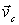-скорость -системы относительно K -системы отсчета. Сложив отдельно левые и правые части этих равенств с учетом того, что 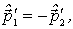получим

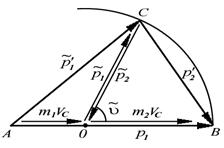
Векторная диаграмма импульсов при столкновении

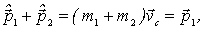
как и должно быть в соответствии с законом сохранения импульса.

Построим теперь векторную диаграмму импульсов. Сначала изобразим вектор 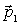отрезком АВ (рис. 4.8), затем векторы 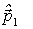и 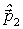, каждый из которых представляет собой, согласно (4.20), сумму двух векторов. Заметим, что это построение справедливо вне зависимости от угла 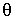. Отсюда следует, что точка С (рис. 4.8) может находиться только на окружности радиуса 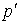с центром в точке О, которая делит отрезок А В на две части в отношении

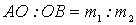. Более того, в рассматриваемом случае, когда частица массы 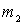покоится до столкновения, эта окружность проходит через точку В - конец вектора 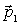, ибо отрезок 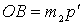. Действительно,

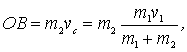
где 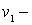скорость налетающей частицы. А тaк как в рассматриваемом случае 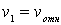, то,

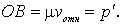
Таким образом, для построения векторной диаграммы импульсов, соответствующей упругому столкновению двух частиц (одна из которых первоначально покоилась), необходимо:

сначала изобразить отрезок АВ, равный импульсу налетающей частицы;

затем через точку B - конец вектора - провести окружность радиуса

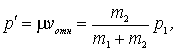
центр которой - точка О - делит отрезок АВ на две части в отношении .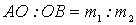

Эта окружность будет геометрическим местом точек всех возможных положений вершины С треугольника импульсов АВС, стороны АС и СВ которого и представляют собой возможные импульсы частиц в K- системе отсчета после столкновения.

В зависимости от соотношения масс частиц точка A - начало вектора 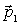может находиться внутри данной окружности, на ней или снаружи. При этом во всех трех случаях угол 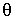может принимать все значения от 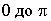. Возможные же значения угла рассеяния налетающей частицы 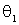и угла разлета частиц 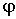будут такими как указано в таблице:

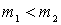
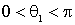
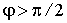
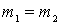
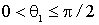
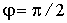
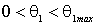
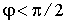
Здесь 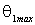- предельный угол. Он определяется формулой

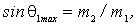
которая непосредственно следует из рис. 4.9 в.

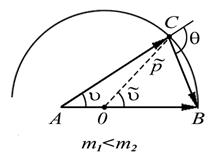
Диаграмма импульсов для случая легкого налетающего тела

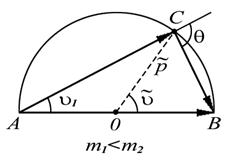
Диаграмма импульсов для равных масс сталкивающихся тел

Кроме того, обнаруживается еще один интересный факт. В последнем случае () под одним и тем же углом 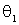возможно рассеяние частицы

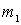как с импульсом АС, так и с импульсом AD, т. е. в этом случае решение неоднозначно. Аналогично обстоит дело и с частицей .

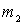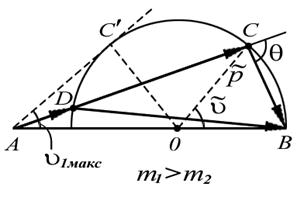
Диаграмма импульсов для случая тяжелого налетающего тела

Из этой же векторной диаграммы импульсов можно найти связь между углами 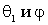. Она дается формулой

.

Этим исчерпываются сведения, которые можно получить о данном процессе столкновения, исходя из одних только законов сохранения импульса и энергии.

Неупругое столкновение - это такое столкновение, в результате которого внутренняя энергия разлетающихся частиц или же одной из них изменяется, а, следовательно, изменяется и суммарная кинетическая энергия системы. Соответствующее приращение кинетической энергии системы можно обозначить через Q. В зависимости от знака Q неупругое столкновение называют экзоэнергетическим (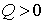) или эндоэнергетическим (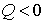). В первом случае кинетическая энергия системы увеличивается, во втором - уменьшается. При упругом столкновении, разумеется, .

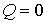Решим задачу об определении возможных импульсов частиц после неупругого столкновения.

Этот вопрос наиболее просто решается в С -системе. Согласно условию, приращение суммарной кинетической энергии системы в данном процессе

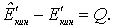
Так как в данном случае 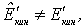то это означает, что импульсы частиц после столкновения изменятся по модулю. Импульс каждой частицы после столкновения 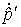легко найти, заменив 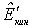в его выражением 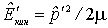. В результате получим

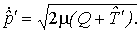
Теперь рассмотрим тот же вопрос в K -системе отсчета, где частица массы 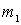с импульсом 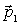испытывает столкновение с покоящейся до столкновения частицей массы 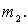Для определения возможных случаев разлета частиц после столкновения здесь также полезно воспользоваться векторной диаграммой импульсов. Ее построение аналогично тому, как это было сделано для упругого столкновения. Импульс налетающей частицы 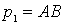делят точкой О на две части, пропорциональные массам частиц

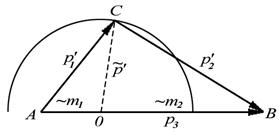
Диаграмма импульсов для неупругого столкновения

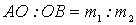(). Затем из точки О проводят окружность радиуса, определяемого формулой. Эта окружность и является геометрическим местом точек всех возможных положений вершины С треугольника импульсов А ВС, стороны АС и СВ которого равны импульсам соответствующих частиц после столкновения.

Отметим, что теперь в отличие от упругого столкновения точка В - конец вектора 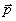- не лежит на окружности, а именно: при Q > 0 эта точка находится внутри окружности, а при Q < 0 - вне ее. Рис. 4.9 соответствует последнему случаю - эндоэнергетическому столкновению.

Итак, пусть необходимо осуществить такое эндоэнергетическое столкновение, в котором внутренняя энергия частиц способна получить приращение не меньше некоторого значения 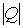. При каком условии такой процесс окажется возможным?

Этот вопрос наиболее просто решается также в С- системе, где ясно, что суммарная кинетическая энергия частиц до столкновения 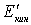во всяком случае должна быть не меньше 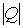, т.е. 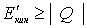. Отсюда следует, что существует минимальное значение 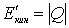, при котором кинетическая энергия системы целиком пойдет на увеличение внутренней энергии частиц и частицы после столкновения остановятся в С -системе.

Рассмотрим этот же вопрос в К -системе отсчета, где частица массы 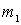налетает на покоящуюся частицу массы 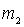. Так как в С -системе при частицы после столкновения останавливаются, то этo значит, что в K -системе при соответствующей пороговой кинетической энергии налетающей частицы 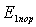обе частицы после столкновения будут двигаться как единое целое, причем с суммарным импульсом, равным импульсу 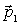налетающей частицы, и кинетической энергией . Поэтому пороговое значение кинетической энергии будет равно

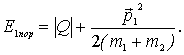
А так как , то, исключив из этих двух уравнений значение импульса налетающей частицы , получим

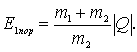
Это и есть та пороговая кинетическая энергия налетающей частицы, начиная с которой данный эндоэнергетический процесс становится энергетически возможным.

Date: 2015-05-19; view: 5562; Нарушение авторских прав