Оператор перестановки частиц. Тождественные частицы. Симметричные и антисимметричные состония. Принцип Паули

Будем называть одинаковыми частицы, имеющие одинаковые массы, заряды, спины и т.д. Такие частицы в равных условиях ведут себя одинаковым образом, теряют свою индивидуальность. Поэтому выполняется принцип тождественности частиц: состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц местами, нельзя различить ни в каком эксперименте и такие состояния следует рассматривать как одно и то же физическое состояние.

Рассмотрим систему из N невзаимодействующих частиц, обладающих спином. Волновая функция такой системы имеет вид 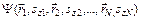. Введем обозначения: 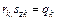, тогда в новых обозначениях волновая функция примет вид: 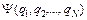. Введем оператор 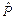перестановки двух частиц местами. Переставим, например, первую и вторую частицы:

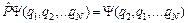. (1)

С другой стороны, по определению оператора:

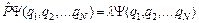. (2)

Подействуем на 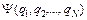оператором 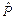дважды, тогда с учетом (1) получим 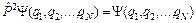, (3)

с учетом (2), получим:

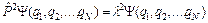(4)

Как следует из (3) и (4), должно выполняться равенство:

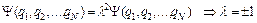
Опр. Функции, сохраняющие свое значение при перестановке аргументов, называются симметричными: 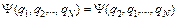. Функции, изменяющие знак при перестановке аргументов, называются антисимметричными: .

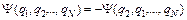В релятивистской квантовой механике доказывается, что частицы с целым спином должны иметь симметричные волновые функции, а частицы с полуцелым спином – антисимметричные. Электроны имеют полуцелый спин, поэтому описываются антисимметричными волновыми функциями.

Частицы с целым спином называются бозонами, с полуцелым – фермионами. Примером бозона является фотон, примерами фермионов – электроны, протоны, нейтроны.

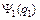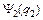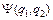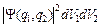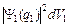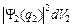Рассмотрим систему из двух невзаимодействующих тождественных фермионов. Каждый из них описывается своей волновой функцией и . Построим из этих функций волновую функцию двух фермионов . Величина определяет вероятность совместного состояния двух фермионов, а величины и – вероятности для состояний для отдельных фермионов. Теорема об умножении вероятностей независимых событий будет выполняться, если двухчастичную волновую функцию записать в виде:

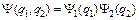. (5)

В силу тождественности фермионов эту функцию можно записать и в виде:

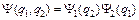. (6)

Так как волновая функция двух фермионов должна быть антисимметричной и следует учесть два варианта представления (5) и (6), то запишем двухчастичную функцию в виде:

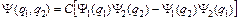, (7)

где С – нормировочный множитель. Функцию (7) можно записать в виде определителя: 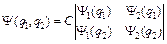. (8)

По аналогии с (8) можно записать волновую функцию для N невзаимодействующих фермионов:

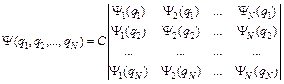. (9)

Рассмотрим случай, когда два фермиона находятся в одинаковых состояниях. Это означает, что среди набора волновых функций две будут одинаковые, например и 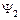. Тогда в определителе (9) два столбца будут совпадать и определитель будет равен нулю. Т.е. такое состояние системы невозможно. Отсюда следует принцип Паули: два тождественных фермиона не могут находиться в одном квантовом состоянии.

Если рассмотреть систему из двух невзаимодействующих бозонов, то двухчастичная волновая функция бозонов запишется в виде:

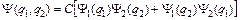. (10)

По аналогии с (10) волновая функция N невзаимодействующих бозонов будет иметь вид:

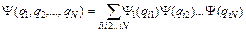, (11)

где суммирование производится по всем перестановкам индексов i1i2….

Многоэлектронный атом. Оператор Гамильтона многоэлектронного атома. Приближение невзаимодействующих частиц. Качественно объяснение структуры периодической таблицы химических элементов.

Полная энергия электронной оболочки многоэлектронного атома состоит из нескольких слагаемых, и отображающий её многоэлектронный гамильтониан атома также включает в себя несколько слагаемых. Это следующие операторы:

Принципы заполнения атомно-орбитальных уровней и построение основных электронных конфигураций: 1) водородоподобие (одноэлектронное приближение в атоме), 2) минимум энергии, 3) принцип Паули, 4) максимальный суммарный спин (1-е правило Хунда). Примеры основных электронных конфигураций легких атомов. Возбужденные атомные конфигурации.

Схема приближенного представления энергии электронного отталкивания в виде энергии экранирования ядра.

Все двухэлектронные слагаемые отталкивания в гамильтониане оболочки атома образуют двумерный косоугольный массив. Их следует просуммировать и приближённо представить суммой, слагаемые которой распределены по отдельным частицам. В таком приближении многоэлектронный гамильтониан примет аддитивный вид. На этом основании можно ввести приближение независимых электронов-"одноэлектронное" приближение.

Date: 2015-05-19; view: 1048; Нарушение авторских прав