Find the Russian equivalents of the following expressions (a-m) in the text above

1. встречаться в природе

2. подвергаться распаду

3. проникающая способность

4. замедлять и снижать

5. cубатомные частицы

6. превращать(ся), преобразовывать(ся)

7. проведенное исследование

8. заряженный положительно

9. траектория

10. увеличиваться на 1

11. приходить в возбужденное состояние

12. избыточная энергия

13. излучать/ выделять

1.3. Find synonyms to the following words in the text above:

1.4. Work in pairs or small groups. Prepare short reports on the following topics connected with radioactive decay:

· Decays with emission of nucleons

· Different modes of beta decay

· Transitions between states of the same nucleus

TEXT 2

Read the text and decide which heading fits each paragraph. There is 1 extra heading that you do not need to use.

1. Measuring half-life

2. Count rate

3. Decay constant

4. Predicting Type of Decay

5. Spontaneous decay

6. Decay graphs and equations

7. Randomness and decay

8. Decay constant and half-life

9. Activity

Radioactive Decay

1____________

Listen to a Geiger counter that is detecting the radial ion from a weak source, so that the count rate is about one count per second. You will notice, of course, that the counts do not come reg­ularly. The counter beeps or dicks in a random, irregular manner. If you try to predict when the next clicks will come, you are unlikely to be right.

You can see the same effect if you have a rate meter, which can measure faster rates. The needle fluctuates up and down. Usually a ratemeter has a control for setting the 'time constant' - the time over which the meter averages out the fluctuations. Usually this can be set to 1 s or 5s. The fluctuations are smoothed out more on the 5s setting.

So it is apparent that radioactive decay is a ran­dom, irregular phenomenon. But is it completely unpredictable? Well, not really. We can measure the average rate of decay. We might measure the number of counts detected in 1000 s, and then calculate the average number per second. We can­not be sure about the average rate, either, because the number of counts in 1000 s will fluctuate, too. So all of our measurements of radioactive decay are inherently uncertain and imprecise.

2 _____________

Radioactive decay occurs within the nucleus of an atom. A nucleus emits radiation, and the atom becomes an atom of a different substance. This is a spontaneous process, which means that we cannot predict, for a particular nucleus, when it will happen. If we sit and stare at an individual nucleus, we cannot see any change that will tell us that it is getting ready to decay. And if it doesn't decay in the first hour when we are watching it, we cannot say that it is any more likely to decay in the next hour. What is more, we cannot affect the probability of an individual nucleus decaying, for example by changing its temperature.

This is slightly odd because it goes against our everyday experience of the way things around us change. We observe things changing. They gradu­ally age, die, rot away. But this is not how things are on the scale of atoms and nuclei. Many of the atoms of which we are made have existed for bil­lions of years and will still exist long after we are gone. The nucleus of an atom does not age.

If we look at a large number of atoms of a radioactive substance, we will see the number of undecayed nuclei gradually decreases. However, we cannot predict when an individual nucleus will decay, each nucleus “makes up its own mind” when to decay, independently from its neighbors. This is because neighboring nuclei do not interact with one another (unlike neighboring atoms). The nucleus is a tiny fraction of the size of the atom, and the nuclear forces do not extend very faroutside the nucleus. So one nucleus can not affect a neighboring nucleus by means of the nuclear force. Being inside a nucleus is a bit like living in a detached house in the middle of nowhere: you can just see out into the garden, hut everything is darkness beyond, and the next house is 1000 km away.

The fact that individual nuclei decay sponta­neously, and independently of their neighbors and of environmental factors, accounts for the random pattern or clicks that we hear from a Geiger counter and the fluctuations of the needle on the ratemeter dial.

3 _____________

Because we cannot say when individual nuclei will decay, we have to start thinking about large numbers of nuclei. Then we can talk about the average number of nuclei that we expect to decay in a particular time interval; in other words, we can find out the average decay rate. Although we cannot make predictions for individual nuclei, we can say that certain nuclei are more likely to decay than others. For example, a nucleus of carbon-12 is stable; carbon-14 decays gradually over thousands of years; carboin-15 nuclei last, on average, a few seconds.

So, because of the spontaneous nature of radioactive decay, we have to make measurements on large numbers of nuclei and then calculate averages. One quantity we can determine is the probability that an individual nucleus will decay in a particular time interval. For example, suppose we observe one million nuclei of a particular radio-isotope. After one hour, 200000 have decayed. Then the probability that an individual nucleus will decay in 1 h is 0.2 or 20%, since 20% of the nuclei have decayed in this time. (Of course, this is only on approximate value, since we might repeat the experiment and find that only 199000 decay. The more times we repeat the experiment, the more reliable our answer will be.)

The probability that an individual nucleus will decay per unit time interval is called the decay constant, symbol λ (lambda). For the example above, we have:

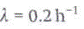
decay constant

Note that, because we are measuring the probability of decay per unit time interval. λ has units of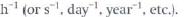

4 ___________

The activity of a radioactive sample is the rate at which nuclei decay. Activity is measured in decays per second 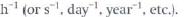An activity of one decay per second is one Becquerel (1 Bq):

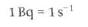
Clearly, the activity of a sample depends on the decay constant λ of the radio-isotope under consideration. The greater the decay constant (the probability that an individual nucleus decays per unit time interval), the greater is the activity of the sample. It also depends on the size of the sam­ple. For a sample of N undecayed nuclei, we have A= λ N

5 _____________

Although we are often interested in finding the activity of a sam­ple of radioactive material, we cannot usually measure this directly. This is because we can­not easily detect all of the radia­tion emitted. Some will escape past our detectors, and some may be absorbed within the sample itself. So our measure­ments give a received count rate R that is significantly lower than the activity A. If we know how efficient our detecting sys­tem is, we can deduce A from R. If the level of background radia­tion is significant, then it must be subtracted to give the cor­rected count rate.

6 ____________

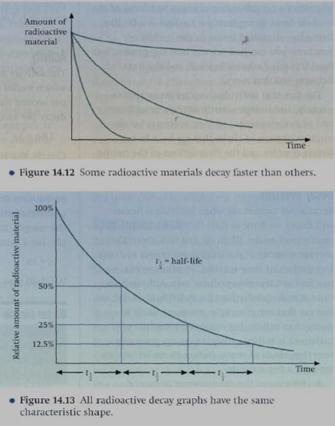
Radioactive substances gradually diminish as time goes by. The atomic nuclei emit radiation and become different substances. The pattern of radioactive decay is an example of a very important pat­tern found in many different situations, a pattern called exponen­tial decay. Figure 14/12 shows the decay graphs for three different radio-isotopes, each with a different rate of decay.

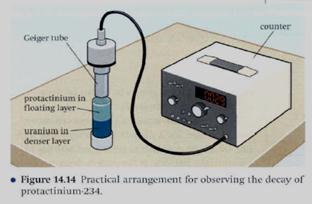
Although the three graphs look different, they all have something in common - their shape. They are curved lines having a special property. If you know what is meant by the half-life of a radio-isotope, then you will understand what is special about the shape of these curves. The half-life t ½ of a radio-isotope is the average (or mean) time taken for half of the nuclei in a sample to decay (Figure 14/13). It takes the same amount of time again for half of the remainder to decay, and a third half-life for half of the new remainder to decay.

In principle, the graph never reaches zero; it just gets closer and closer. (In practice, when only a few undecayed nuclei remain, it will cease to be a smooth curve and will eventually reach zero.) We use the idea of half-life, because we cannot say when a sample will have completely decayed.

7 _____________

If you are to measure the half-life of a radioactive substance in the laboratory, you need to choose something that will not decay too quickly or too slowly. In practice, the most suitable radio-isotope is protactinium-234, which decays by emitting ir­radiation. This is produced in a bottle containing uranium (Figure 14/14). By shaking the bottle, you can separate the protactinium into the top layer of solvent in the bottle. The Geiger counter allows you to measure the decay of the protactinium.

After recording the number of counts in consec­utive 10-second intervals over a period of a few minutes, you can then draw a graph, and use it to find the half-life of protactinium-234.

8 _____________

A radio-isotope that decays rapidly has a short half-life t ½. Its decay constant must be high, since the probability per unit time of an individual nucleus decaying must be high. Hence there is a connection between half-life and decay constant. They are inversely related by the expression

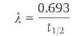
(The constant 0.693 comes in to this because 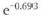= ½, approximately.)

Thus if we know either t ½ or λ, we can calcu­late the other. For a nuclide with a very long half-life, we might not wish to sit around waiting to measure the half-life: it is easier to determine λ by measuring the activity (and using A= λ N), and then deduce t ½.

Note that the units of λ and t ½ must be compatible; for example, λ in s‾¹ and t ½ in s.

2.2. Work in pairs. Using information from the text say a few words about:

1. Geiger counter

2. Time constant

3. Decay constant

4. Exponen­tial decay

5. Half-life of a radio-isotope

2.3. Match the notions and their definitions:

1. ion a) the microwave radiation pervading the universe that exhibits a corresponding blackbody temperature of 2.7 K and that is the principal evidence supporting the big bang theory

2. ratemeter b) a form of a chemical element which sends out radiation

3. fluctuations c) a line defined by an equation so that the coordinates of its points are functions of a single independent variable or parameter

4. radio-isotope d) an instrument that indicates the counting rate of an electronic counter

5. detector e) a decrease that follows an exponential function

6. constant f) a number or quantity that does not vary

7. background radia­tion g) an atom or a molecule with a positive or negative electric charge caused by its losing or gaining one or more electrons

8. exponen­tial decay h) a piece of equipment for discovering the presence of smth, such as metal, smoke, explosives or changes in pressure or temperature

9. curve i) frequent changes in size, amount, quality, etc., especially from one extreme to another

Date: 2015-05-18; view: 511; Нарушение авторских прав