Основные положения метода конечных элементов

Метод конечных элементов основан на аппроксимации искомой непрерывной функции (электрического потенциала, векторного магнитного потенциала и др.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых конечными элементами (КЭ). В качестве функции конечного элемента используют полином.

Основные положения метода конечных элементов удобно рассмотреть на решении двумерных краевых задач, которые делятся на плоскопараллельные и осесимметричные.

Плоскопараллельные краевые задачи используют декартову систему координат 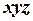, причем предполагается, что геометрия расчетных областей, свойства сред и параметры, характеризующие источники поля неизменны в направлении оси 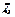. Вследствие этого описание геометрии электротехнического устройства, задание свойств, граничных условий и источников поля можно проводить плоскости 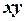, называемой плоскостью модели.

Осесимметричные задачи решаются в цилиндрической системе координат 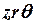. Порядок следования осей выбирается для общности с плоскопараллельными задачами. Физические свойства и источники поля предполагаются не зависящими от угловой координаты. Работа с моделью проводится в плоскости .

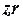Применение метода конечных элементов начинается с разбиения области моделирования 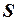на конечные элементы, причем их число, размеры и расположение произвольны. Конечные элементы могут представлять собой треугольники. Стороны треугольников должны совпадать с границами раздела сред с различными свойствами.

Если воспользоваться примером плоскопараллельной задачи расчета магнитного поля постоянного тока методом конечных элементов, то внутри каждого элемента векторный магнитный потенциал 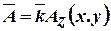можно представить в виде интерполяционного полинома первой степени

.

Конечный элемент, внутри которого функция 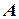представлена интерполяционным полиномом первой степени, называется двумерный симплекс-элемент (рис. 1.1). Это треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине. В треугольнике, как правило, используется последовательная нумерация узлов против часовой стрелки, начиная от некоторого узла с номером 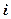, который выбирается произвольно. Узловые значения искомой величины 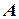обозначаются через 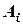, 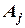и 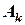, а координаты трех узлов соответственно есть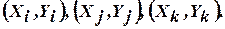

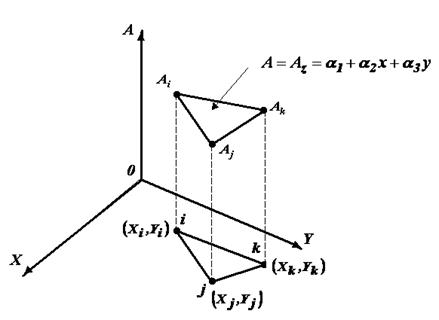
Рис. 1.1. Двумерный симплекс - элемент

В узлах конечного элемента выполняются следующие условия:

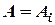при , ,

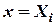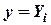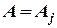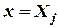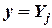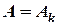при , ,

при , .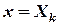

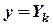Подстановка этих условий в интерполяционный полином приводит к системе уравнений

,

,

.

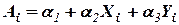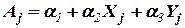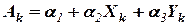В результате решения системы уравнений можно определить коэффициенты

,

,

.

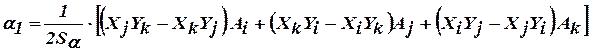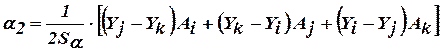Определитель системы связан с площадью треугольника 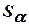соотношением

.

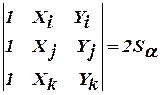Подставляя значения 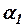, 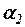и 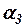в интерполяционный полином, можно записать выражение для функции 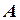через три функции формы, по одной для каждого узла

.

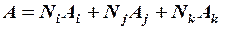В матричном виде

где 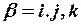– номера узлов (вершин) треугольника.

Для каждого узла функция формы (пробная функция) выглядит следующим образом:

,

,

,

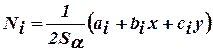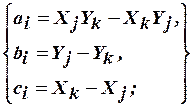
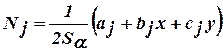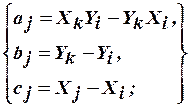
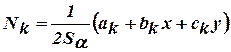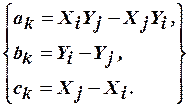
Значение функции формы 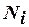в узле с номером :

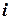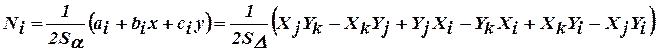
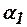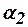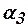Выражение в скобках представляет собой величину определителя системы уравнений относительно , и , поэтому в узле с номером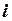

.

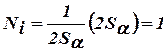Можно доказать, что 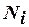равно нулю в узлах с номерам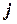и и 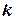, так же как и во всех точках прямой, проведенной через эти узлы.

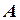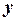Величина определяется внутри конечного элемента функциями формы, линейными по и , поэтому градиенты этой величины в направлениях 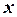и 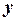будут постоянны. Например, градиент в направлении определяется соотношением

.

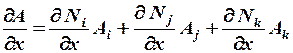Учитывая, что

, ,

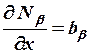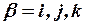можно записать

.

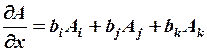В этом выражении коэффициенты 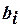, , 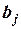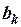являются постоянными (они фиксированы, если заданы узловые координаты). Узловые значения искомой функции 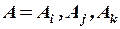также не зависят от пространственных координат, поэтому частная производная на конечном элементе имеет постоянное значение.

Постоянство градиента внутри каждого элемента означает, что необходимо использовать очень малые по величине конечные элементы, чтобы аппроксимировать быстро меняющуюся функцию .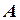

Решение краевых задач теории поля методом конечных элементов производится на основе вариационного исчисления. С вариационной точки зрения решение дифференциального уравнения в частных производных с заданными граничными условиями эквивалентно нахождению минимума функционала, составленному из энергетических соотношений поля.

Для плоскопараллельного магнитного поля постоянного задача решение уравнения Пуассона относительно векторного магнитного потенциала 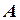в методе конечных элементов можно заменить задачей определения функции 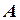, доставляющей минимум функционалу вида:

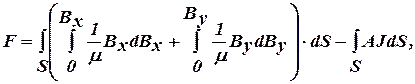
где 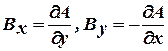- составляющие вектора магнитной индукции поля, распределенного в области 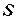по осям и .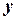

Записав условие минимума функционала, являющегося функцией значений 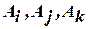на каждом конечном элементе, получим систему алгебраических уравнений для определения значений 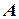в вершинах (узлах) треугольников, которыми покрывается расчетная область :

,

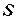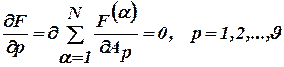где 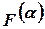- вклад треугольника 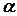в общий функционал, 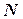- число треугольников (конечных элементов), 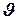- число неизвестных (вершин треугольников).

Для каждого треугольника можно получить выражения:

Аналогичным образом определятся

,

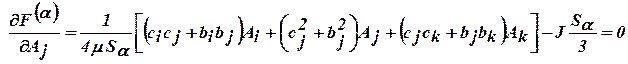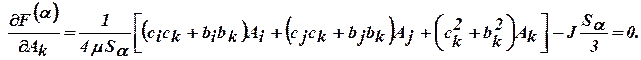
На основе полученных уравнений для каждого конечного элемента (треугольника) образуется система алгебраических уравнений, решение которой дает значения векторного магнитного потенциала 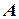в вершинах треугольников. Система алгебраических уравнений будет линейной, если в кусочно-однородных подобластях магнитная проницаемость среды принимается постоянной величиной, то есть задается 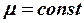, в противном случае – система алгебраических уравнений является нелинейной.

Классическим методом решения системы линейных алгебраических уравнений является метод Гаусса. Это метод последовательного исключения неизвестных, когда с помощью элементарных преобразований система уравнений приводится к системе треугольного вида, из которого последовательно, начиная с последних (по номеру) неизвестных находятся все остальные.

Наиболее известным методом решения системы нелинейных алгебраических уравнений является метод Ньютона. Этот метод основан на принципах простой итерации. При этом решение системы нелинейных алгебраических уравнений заменяется последовательным решением системы линейных алгебраических уравнений на каждой итерации методом Гаусса.

В методе конечных элементов для решения краевой задачи расчета поля применяются также другие способы. Преимуществом этих способов является то, что отправной точкой для них служит непосредственно само дифференциальное уравнение, и кроме того они исключают необходимость вариационной формулировки физической задачи поиска функционала из энергетических соотношений. Среди способов наиболее известным является метод Галеркина. Этот метод предусматривает приближенное решение дифференциального уравнения, описывающее поле, распределенного области 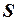. При этом должно выполняться следующее условие: разность между приближенным и точным решениями должна быть ортогональна функциям формы, используемым при аппроксимации.

Применение метода Галеркина в сочетании с методом конечных элементов, например, для расчета плоскопараллельного магнитного поля переменных синусоидальных токов приводит к уравнениям вида

,

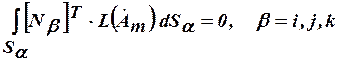где 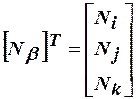- транспонированная матрица функций формы;

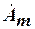- искомая величина (комплексная амплитуда векторного магнитного потенциала, имеющая в плоскопараллельной задаче одну составляющую в направлении оси 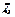), которая представлена соотношением

.

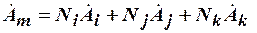В подынтегральном выражении уравнение

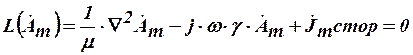
является дифференциальным уравнением, определяющим значения искомой величины 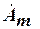в вершинах треугольника с номерами .

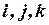Для плоскопараллельной задачи расчета магнитного поля переменных синусоидальных токов

,

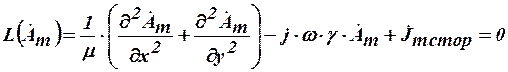где 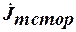- комплексная амплитуда плотности сторонних токов, ориентированных в направлении оси 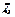; 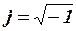- мнимая единица.

В результате интегрирования уравнений вида

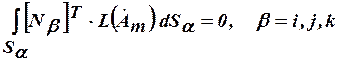
на каждом конечном элементе 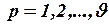можно получить систему алгебраических уравнений для определения комплексных значений векторного магнитного потенциала во всех узлах (вершинах) 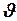треугольников, покрывающих расчетную область .

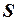Применение метода конечных элементов для задач электростатики и электрического поля постоянных токов в проводящей среде осуществляется аналогичным образом, но при этом искомой функцией является электрический потенциал , значения которого в вершинах треугольников подлежат определению решением системы алгебраических уравнений.

Date: 2015-05-18; view: 2323; Нарушение авторских прав