
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Электромагнитное поле и уравнения Максвелла
|
|
К основным понятиям теории электромагнитного поля относятся: электрическое поле, магнитное поле и электромагнитное поле.
Электрическое поле является составной частью электромагнитного поля. Оно создается совокупностью электрических зарядов. Электрическое поле обладает способностью воздействовать на помещенный в него электрический заряд механической силой, прямо пропорциональной величине этого заряда. Если заряды, создавшие электрическое поле, неподвижны, то поле называется электростатическим.
Магнитное поле является составной частью электромагнитного поля. Оно создается совокупностью движущихся зарядов. Магнитное поле обладает способностью воздействовать на помещенный в него проводник с током механической силой, прямо пропорциональной силе тока.
Электромагнитное поле есть совокупность электрического и магнитного полей в их взаимной связи. Изменение во времени одного из полей (электрического или магнитного) влечет за собой изменение другого поля. При угасании одного поля, исчезает и другое. Если существует взаимная связь между электрическим и магнитным полями, то существует и электромагнитное поле.
При рассмотрении электромагнитного поля используются следующие его характеристики:
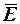 - вектор напряженности электрического поля;
- вектор напряженности электрического поля;
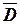 - вектор электрического смещения;
- вектор электрического смещения;
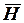 - вектор напряженности магнитного поля.
- вектор напряженности магнитного поля.
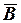 - вектор индукции магнитного поля;
- вектор индукции магнитного поля;
Причем векторы 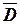 и
и 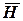 не зависят от физической природы материальной среды и ее свойств, что существенно облегчает задачу расчета электромагнитного поля Векторы
не зависят от физической природы материальной среды и ее свойств, что существенно облегчает задачу расчета электромагнитного поля Векторы 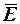 и
и 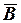 , наоборот, зависят от свойств материальной среды, и являются силовыми характеристиками поля.
, наоборот, зависят от свойств материальной среды, и являются силовыми характеристиками поля.
Задача расчета электромагнитного поля заключается в определении характеристик поля в каждой точке рассматриваемой части пространства, где поле существует.
Для исследования электромагнитного поля применяются законы электротехники, которые могут быть представлены в двух формах записи: интегральной и дифференциальной. Интегральная форма записи законов электротехники применяется для конечных контуров, площадей, объемов проводящих сред и диэлектриков.
В интегральной форме записи эти законы имеют вид:
· Закон Ома 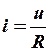 .
.
· Закон Джоуля-Ленца 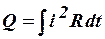 .
.
· Первый закон Кирхгофа 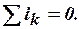
· Второй закон Кирхгофа 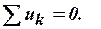 .
.
· Закон электромагнитной индукции 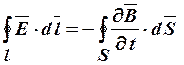
· Закон полного тока 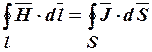 .
.
· Теорема Гаусса 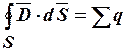 .
.
Дифференциальная форма записи законов электротехники применяется для определения характеристик электромагнитного поля:
· Закон Ома 

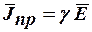 .
.
· Закон Джоуля - Ленца 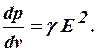
· Первый закон Кирхгофа 
· Второй закон Кирхгофа 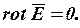
· Закон полного тока 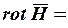
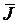 .
.
· Закон электромагнитной индукции 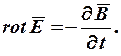
· Теорема Гаусса 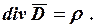
Приведенные уравнения законов электротехники являются инвариантными по отношению к любой выбранной (прямоугольной, цилиндрической или сферической) системе координат.
На основе законов электротехники составляется полная система уравнений Максвелла, с помощью которой в общем случае описываются все электромагнитные поля.
Полную систему уравнений Максвелла записывают в дифференциальной и интегральной форме.
 Дифференциальная форма Интегральная форма
Дифференциальная форма Интегральная форма
где 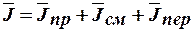 - вектор плотности полного тока, имеющая три составляющих:
- вектор плотности полного тока, имеющая три составляющих: 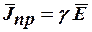 - вектор плотности тока проводимости;
- вектор плотности тока проводимости; 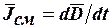 - вектор плотности тока смещения;
- вектор плотности тока смещения; 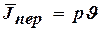 - вектор плотности тока переноса;
- вектор плотности тока переноса; 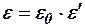 - абсолютная диэлектрическая проницаемость среды,
- абсолютная диэлектрическая проницаемость среды, 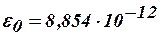
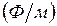 – электрическая постоянная вакуума (воздуха),
– электрическая постоянная вакуума (воздуха), 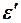 - относительная диэлектрическая проницаемость среды;
- относительная диэлектрическая проницаемость среды; 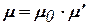 - абсолютная магнитная проницаемость среды;
- абсолютная магнитная проницаемость среды;  (Гн/м) - магнитная постоянная вакуума (воздуха).
(Гн/м) - магнитная постоянная вакуума (воздуха).
Эти уравнения являются исходными при изучении теории электромагнитного поля.
Если свойства среды, определяемые коэффициентами 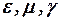 , неизменны, то все записанные уравнения будут линейными. Этому условию соответствует принцип суперпозиции, согласно которому поле, образованное несколькими источниками, представляет собой сумму полей каждого из источников, существующих в тех же условиях отдельно.
, неизменны, то все записанные уравнения будут линейными. Этому условию соответствует принцип суперпозиции, согласно которому поле, образованное несколькими источниками, представляет собой сумму полей каждого из источников, существующих в тех же условиях отдельно.
При изучении электромагнитных полей различных типов стараются ввести понятие потенциальной функции  (потенциала) поля, которая является скалярной характеристикой векторного поля, например, под потенциалом электростатического поля понимается скалярная энергетическая характеристика, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.
(потенциала) поля, которая является скалярной характеристикой векторного поля, например, под потенциалом электростатического поля понимается скалярная энергетическая характеристика, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.
Для потенциала также выполняется принцип суперпозиции (наложения): результирующий потенциал системы источников поля складывается из потенциалов отдельных источников.
Электромагнитные поля разбиваются на классы. Простейшими являются неизменные во времени поля – статические (электростатические и магнитостатические), а также стационарные переменные поля, изменяющиеся во времени по синусоидальному закону.
Для электростатических полей, обусловленных действием неподвижных электрических зарядов, справедливы уравнения:
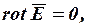
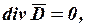
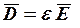 .
.
Потенциальная функция  связана с напряженностью поля
связана с напряженностью поля 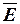 соотношением:
соотношением:
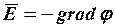 .
.
В декартовой системе координат
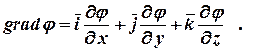
В цилиндрической системе координат
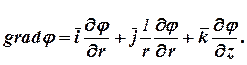
В однородной среде 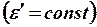 для потенциала справедливо уравнение Пуассона
для потенциала справедливо уравнение Пуассона
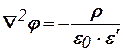
и в частности, где отсутствуют свободные заряды 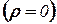 , уравнение Лапласа
, уравнение Лапласа
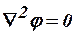 .
.
Уравнение Пуассона в декартовой системе координат:
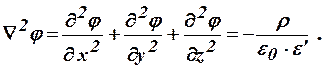
Уравнение Пуассона в цилиндрической системе координат
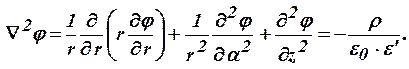
Для нахождения потенциала  в уравнениях Лапласа и Пуассона следует задаться граничными условиями.
в уравнениях Лапласа и Пуассона следует задаться граничными условиями.
Граничные условия определяют поведение векторов поля (нормальных и тангенциальных составляющих) на границе раздела двух сред, параметры которых меняются скачком.
Для всех электрических полей имеют место основные граничные условия, которые являются прямым следствием системы уравнений Максвелла.
 ;
;
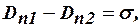
где 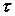 означает тангенциальную составляющую проекции вектора к границе раздела двух сред, а
означает тангенциальную составляющую проекции вектора к границе раздела двух сред, а 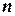 - нормальную составляющую. При этом предполагается, что нормаль к поверхности раздела двух сред
- нормальную составляющую. При этом предполагается, что нормаль к поверхности раздела двух сред 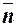 направлена из первой среды во вторую. Символом
направлена из первой среды во вторую. Символом 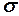 обозначают поверхностную плотность свободных зарядов, имеющую размерность
обозначают поверхностную плотность свободных зарядов, имеющую размерность 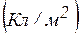 , такую же, что у вектора плотности электрического смещения
, такую же, что у вектора плотности электрического смещения 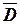 .
.
Если на границе раздела двух диэлектриков плотность свободного поверхностного заряда 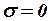 , то выполняется условие
, то выполняется условие
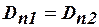 или
или 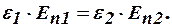
В диэлектрике кроме векторов 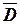 и
и 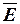 рассматривают вектор поляризации вещества
рассматривают вектор поляризации вещества 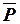 , который связан с основными векторами поля выражением
, который связан с основными векторами поля выражением
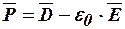 или
или 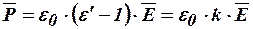 ,
,
где 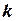 - диэлектрическая восприимчивость вещества.
- диэлектрическая восприимчивость вещества.
На границе раздела двух диэлектриков возникает связанный электрический заряд. Поверхностная плотность 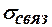 связанного заряда определяется выражением
связанного заряда определяется выражением
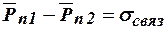 .
.
На поверхности проводящего тела вектор электрического смещения 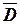 изменяется скачком на величину поверхностной плотности свободного заряда в данной точке, а направление вектора совпадает с направлением внешней нормали к поверхности проводника
изменяется скачком на величину поверхностной плотности свободного заряда в данной точке, а направление вектора совпадает с направлением внешней нормали к поверхности проводника 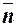 .
.
Поле внутри проводника равно нулю 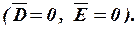
На поверхности проводника выполняются граничные условия
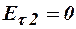 и
и 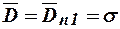 .
.
Граничным условием Неймана называется условие
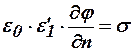 .
.
Поверхность проводника 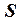 является эквипотенциальной поверхностью. На поверхности проводника выполняется граничное условие Дирихле
является эквипотенциальной поверхностью. На поверхности проводника выполняется граничное условие Дирихле
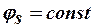 .
.
Энергия системы заряженных тел определяется выражением
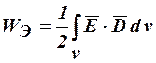 .
.
Емкость системы заряженных тел с зарядами 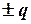 и напряжением между ними
и напряжением между ними 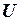 есть
есть
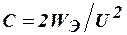 .
.
Силу, действующую на заряженное тело, можно найти, пользуясь одним из выражений 
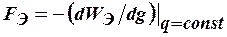 ,
, 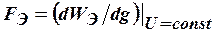 ,
,
где 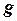 - обобщенная координата, по которой может перемещаться тело под действием силы.
- обобщенная координата, по которой может перемещаться тело под действием силы.
Электрическое поле постоянных токов в проводящей среде описывается системой уравнений:
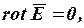
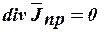 ,
,
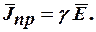
Электрическое поле постоянного тока является потенциальным и может быть определено потенциальной функцией
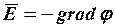 .
.
В однородной проводящей среде электропроводностью 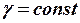
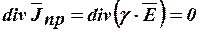 , отсюда
, отсюда 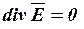 , следовательно, потенциал электрического поля удовлетворяет уравнению Лапласа.
, следовательно, потенциал электрического поля удовлетворяет уравнению Лапласа.
На границе раздела двух проводящих сред выполняются условия
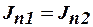
или для напряженности электрического поля
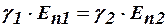 ,
,
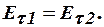
Магнитное поле постоянных токов удовлетворят системе уравнений
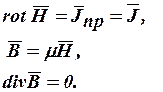
В части пространства, где нет тока 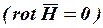 , можно использовать скалярный магнитный потенциал
, можно использовать скалярный магнитный потенциал
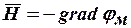 .
.
Использование векторного магнитного потенциала 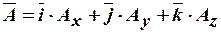 соотношением
соотношением 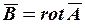 приводит к уравнению
приводит к уравнению  , которое в однородной среде с магнитной проницаемостью
, которое в однородной среде с магнитной проницаемостью 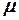 в прямоугольной системе координат удовлетворяет уравнению Пуассона:
в прямоугольной системе координат удовлетворяет уравнению Пуассона:
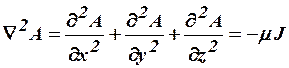 ,
,
где 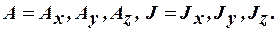
Магнитный поток связан с векторным магнитным потенциалом соотношением
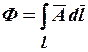 .
.
Выражение
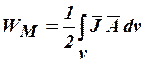
позволяет найти энергию магнитного поля токов плотностью 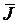 , протекающих в объеме
, протекающих в объеме 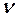 . При этом индуктивность проводников с током
. При этом индуктивность проводников с током 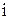 определяется выражением
определяется выражением
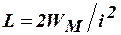 .
.
Электромагнитная сила определяется по одному из выражений
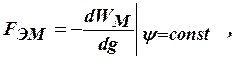
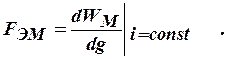
Электромагнитная сила, действующая на уединенный контур с током 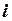 , определяется выражением
, определяется выражением
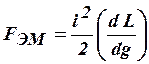 .
.
На границе раздела двух сред с различными магнитными проницаемостями 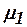 и
и 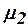 выполняется условие:
выполняется условие:
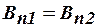
или для напряженности магнитного поля
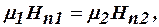
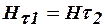 ,
,
где 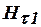 и
и 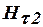 - касательные составляющие вектора
- касательные составляющие вектора 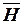 ;
; 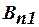 и
и 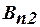 – нормальные составляющие вектора магнитной индукции
– нормальные составляющие вектора магнитной индукции 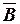 в точках, примыкающих к границе в одном месте, но с разных сторон.
в точках, примыкающих к границе в одном месте, но с разных сторон.
Задача расчета магнитного поля переменных синусоидальных токов состоит в расчете магнитного и электрического поля в линейной и нелинейной (ферромагнитной) среде с учетом вихревых токов (поверхностный эффект) и формулируется как дифференциальное уравнение в частных производных относительно комплексной амплитуды векторного магнитного потенциала:

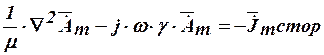 ,
,
где 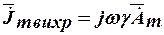 - плотность вихревого тока, индуцированного переменным магнитным полем в проводящей среде, имеющей электропроводность
- плотность вихревого тока, индуцированного переменным магнитным полем в проводящей среде, имеющей электропроводность  ;
; 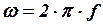 - угловая частота;
- угловая частота; 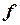 - частота синусоидального тока;
- частота синусоидального тока; 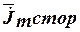 - комплексная амплитуда плотности стороннего тока, вызванного приложенным извне напряжением.
- комплексная амплитуда плотности стороннего тока, вызванного приложенным извне напряжением.
1.2. ТЕОРЕМА ЕДИНСТВЕННОСТИ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ
Расчеты электрического и магнитного полей представляют собой разновидности решения краевой задачи, которая формулируется как уравнение Лапласа и Пуассона в исследуемом пространстве, состоящем из кусочно-однородных областей, характеризующихся постоянными параметрами среды 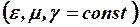 . Уравнение Лапласа и Пуассона в этих кусочно-однородных областях является линейным дифференциальным уравнением в частных производных второго порядка.
. Уравнение Лапласа и Пуассона в этих кусочно-однородных областях является линейным дифференциальным уравнением в частных производных второго порядка.
В общем случае уравнение Лапласа и Пуассона может иметь бесчисленное множество решений.
Теорема единственности решения краевой задачи показывает, что единственное решение уравнения Лапласа и Пуассона получается, если на границе области, в которой рассматривается это уравнение, заданы граничные условия:
· первого рода (задача Дирихле), когда на границе области считается известной искомая функция;
· второго рода (задача Неймана), когда на границе области считается известной нормальная производная искомой функции;
· третьего рода – смешанные граничные условия, когда на границе расчетной области считается известной искомая функция, а на других границах ее нормальная производная.
Современная математика располагает многими аналитическими и численными методами решения краевых задач, а современное математическое обеспечение персональных компьютеров содержит в своем составе «решатели» краевых задач для уравнений Лапласа и Пуассона.
Date: 2015-05-18; view: 3732; Нарушение авторских прав