Сепарационные характеристики

Под сепарационной характеристикой понимают зависимость вероятности излечения частиц в какой либо продукт сепарации от разделительного признака. Сепарационная характеристика показывает разделительную способность обогатительного аппарата. Одним из ее основных свойств является постоянство при изменении в некоторых пределах состава сепарируемого материала.

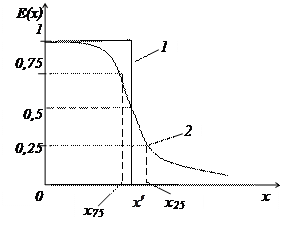
Рис.5.2. Сепарационная характеристика: 1- идеальная; 2- реальная

Она является основой для выбора обогатительного аппарата и его конструктивных и режимных параметров, а также для выполнения технологических расчетов. На рис.5.2 показан общий вид сепарационной характеристики для извлечения, например, в легкий продукт при гравитационной сепарации.

Идеальная сепарационная характеристика обеспечивает разделение смеси частиц по граничному значению разделительного признака 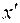с полным извлечением (Е=1) в целевой продукт целевого компонента (частиц с 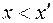). При этом частицы не целевого компонента (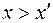) в целевой продукт не извлекаются (Е=0).

Граничным значением разделительного признака будет такое, при котором соответствующая ему бесконечно узкая фракция частиц распределяется равновероятно между продуктами сепарации. Т.е. ее извлечения в любой продукт составляет 0,5 (рис.5.2).

В реальном процессе сепарации происходит засорение продуктов разделения посторонними фракциями. Это происходит вследствие возникновения помех процессу сепарации, связанных с гидродинамическим режимом обогатительного аппарата, турбулентностью, взаимным влиянием движущихся частиц и другими причинами, связанными с особенностью используемых сепарационных эффектов и организацией процесса сепарации.

Общим подходом для определения сепарационных характеристик является баланс каждой узкой фракции сепарируемых частиц, т.е. сумма потоков частиц в продуктах сепарации равен входному потоку 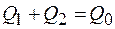, откуда вероятность извлечения частиц в продукты сепарации:

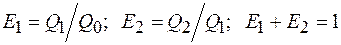
Если продукты сепарации представляют собой двухфазные системы (суспензия, гидросмесь),то поток частиц в том или ином продукте сепарации равен произведению объемного расхода на концентрацию в нем частиц, т.е. .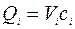

Определение концентраций является весьма сложной задачей, поскольку оно связано с точностью математической процесса сепарации. Для некоторых процессов сепарации аналитическое определение сепарационных характеристик будет представлено в соответствующих разделах.

В практике обогащения полезных ископаемых, полагая, что ошибки при сепарации подчиняются нормальному закону распределения случайной величины, широко используется описание сепарационных характеристик с помощью интеграла вероятности Гаусса:

.

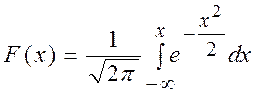Значение параметра х представляет собой отклонение средней плотности фракции 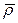от плотности разделения 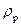в долях среднеквадратичного отклонения.

Для гравитационных процессов сепарации: 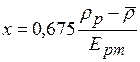, где 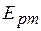- среднее вероятное отклонение плотности разделения.

Значение интеграла вероятности Гаусса может быть определено по специальным таблицам.

Вычисление интеграла вероятности Гаусса возможно также по приближенной формуле, обеспечивающей точность расчетов до 10^-6:

,

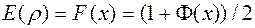где Ф(х) функция Лапласа, определяемая формулой 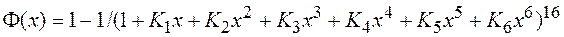при следующих значениях коэффициентов:

К₁=4,986735^.10^-2;

К₂=2,114101^.10^-2;

К₃=3,277626^.10^-3;

К₄=3,8004^.10^-4;

К₅=4,8891^.10^-5;

К₆=5,383^.10^-6.

Используемый в данном случае нормальный закон распределения случайной величины двухпараметрический. Параметры этого распределения: математическое ожидание (здесь граничное значение разделительного признака) и среднее квадратичное отклонение или среднее вероятное отклонение. Если эти параметры известны, то и описание сепарационной характеристики будет вполне определенным.

Date: 2015-05-18; view: 2185; Нарушение авторских прав