Методические указания. Для выполнения данного пункта краткие пояснения даны ниже

Для выполнения данного пункта краткие пояснения даны ниже.

Для трехпроводной линии, расположенной в воздухе параллельно поверхности земли справедливы группы формул Максвелла.

Первая группа формул:

,

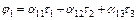
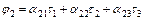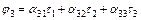
(4.1)

где 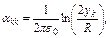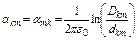- собственные и взаимные потенциальные коэффициенты (м/Ф) соответственно, причем k¹m;

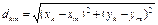- расстояние между k и m проводами (м);

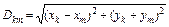- расстояния между k проводом и зеркальным изображением m провода (м);

и 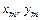- координаты проводов; R – радиус проводов (м);

- потенциалы проводов (В);

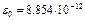(Ф/м);

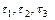- линейные плотности зарядов проводов (Кл/м).

По заданным координатам проводов и известном R=0.02 м рассчитываются собственные 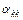и взаимные 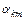потенциальные коэффициенты проводов линии.

Вторая группа формул:

,

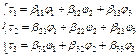(4.2)

где

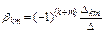- собственные (k=m) и взаимные (k¹m) емкостные коэффициенты (Ф/м);

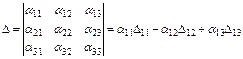
-определитель системы уравнений (4.1);

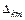- минор, образованный вычеркиванием k строки и m столбца определителя D, например:

= .

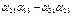По предварительно полученным потенциальным коэффициентам рассчитываются собственные и взаимные емкостные коэффициенты.

Затем по формулам (4.2) находятся линейные плотности зарядов проводов .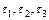

Третья группа формул:

,

(4.3)

где

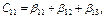
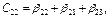
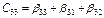
- собственные частичные емкости (Ф/м);

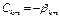- взаимные частичные емкости при k¹m (Ф/м).

По предварительно найденным емкостным коэффициентам определяются частичные емкости. Далее необходимо сделать проверку правильности расчета линейных плотностей зарядов проводов и их коэффициентов. Для этого в систему (4.1) подставляются найденные величины (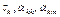) и определяются потенциалы проводов 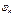, которые сравниваются с заданными значениями.

Энергию электростатического поля на единицу длины линии (Дж/м) можно рассчитать по формуле:

Для точки N с заданными координатами x,y потенциал j и вектор напряженности 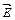определяются методом наложения с учетом зеркальных изображений проводов линии:

; ,

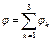где

- составляющая потенциала, создаваемая зарядом k провода и его зеркальным изображением (В);

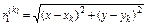- расстояние от точки N до k провода (м);

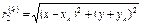- расстояние от точки N до зеркального изображения k провода (м);

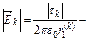модуль вектора напряженности (В/м), создаваемый зарядом k провода;

модуль вектора напряженности (В/м), создаваемый зеркальным изображением заряда k провода.

Потенциал j равен алгебраической сумме составляющих потенциала 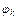, причем числовые значения 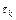подставляются со своими знаками. Вектор напряженности 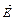необходимо определить графическим сложением векторов 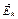и 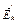от всех зарядов и их зеркальных изображений, которые направлены вдоль радиусов 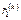и 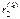соответственно, причем при 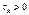вектор 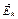направлен от k провода и вектор 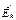направлен к зеркальному изображению провода, а при 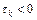направления векторов 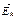и 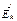меняются на противоположные.

Контрольные вопросы

1. Как определяются потенциальные коэффициенты трехпроводной линии?

2. Как определяются емкостные коэффициенты трехпроводной линии?

3. Какие коэффициенты всегда отрицательны?

4. Как определяется электрическая емкость между двумя телами? Как влияет на емкость поверхность земли?

5. Как графически изображается картина электростатического поля?

6. Расскажите применение метода зеркального изображения для трехпроводной линии?

Date: 2015-05-18; view: 373; Нарушение авторских прав