С возмущенным потенциалом

Возмущение 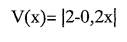задается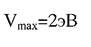

Тогда яма имеет вид:

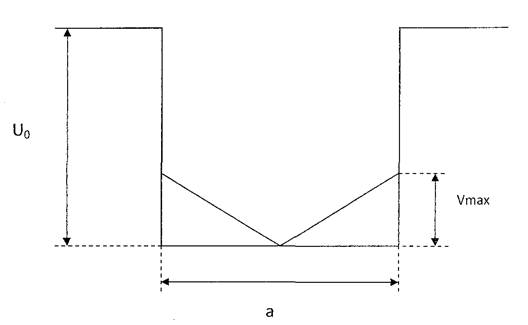
Потенциальная энергия частицы в такой яме равна:

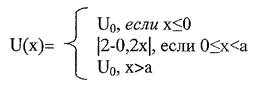
Дана потенциальная 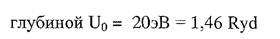яма шириной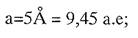

Вычисление матричного элемента. Матричный элемент вычислим по формуле:

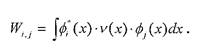22

Так как все волновые функции «невозмущенной» задачи оказались действительными, то для всех волновых функций:

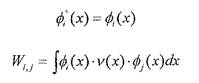
Формально, интеграл должен быть вычислен по всей области определения волновых функций, то есть

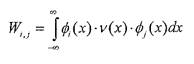
В то же время известно, что при х<0 и при х>а1 все волновые функции равны нулю, поэтому и интегралы по соответствующим областям также равны нулю. Теперь

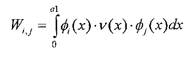
Длину интегрирования выбираем равной 10 Отсюда:

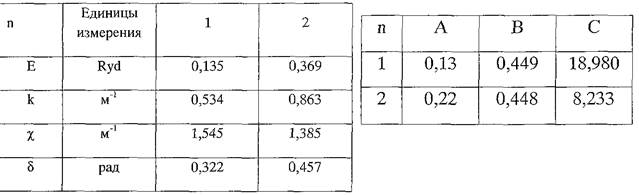
Значение матричных элементов:

Поправки к энергиям:

Для первого энергетического уровня:

24

Для второго энергетического уровня:

5. Выводы

В ходе решения задачи без возмущения, получили подтверждение квантования энергии частицы в связанных состояниях, ото иллюстрируется графиках:*! решений трансцендентных уравнений.

Так же из построенных графиков решений трансцендентных уравнении видно, что- с увеличением глубины потенциальной ямы увеличивается число энергетических уровней, но расстояние между этими уровнями не изменяется

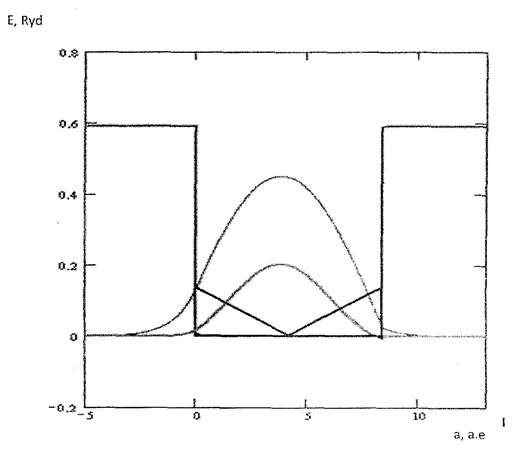
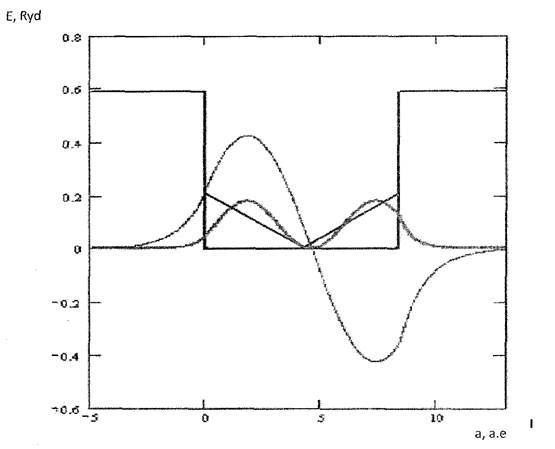
Из графиков волновых функций и графиков распределения плотности вероятности невозмущенной задачи видно, что в низшем (основном) энергетическом состоянии п=1 с наибольшей вероятностью частицу можно обнаружить в середине ямы. а вероятность нахождения ее в близи краев ямы весьма мала. Такое поведение часгицы резко отличается от поведения классической частицы, которая совершала бы н такой яме финитные движения. С увеличением энергии (то есть с ростом квантового числа п) максимумы распределения плотности вероятности располагаются все ближе друг к Другу, а значит можно сделать вывод, что при очень больших значениях п картина распределения плот нести вероятности практически «сольется», т.е. квантовая частица начнет вести себя как классическая.

При анализе поправок к энергиям потенциальной ямы с возмущением установлено, что каждая последующая поправка является малой но сравнению с предыд) щей. то есть ряд сходится. А значит, в условиях данной задачи можно использовать метод теории возмущений.

Из исследования энергий, с учетом поправок, потенциальных ям различной ]дубины установлено, что с увеличением глубины потенциальной ямы растет влияние возмущения на значения энергий. Это связано с тем, что возмущение зависит от глубины ямы (чем больше глубина ямы, тем больше возмущение), а значения энергии в пулевом приближении одинаковы для ям различной глубины.

Так же замечено, что наибольшее влияние возмущение оказывает на энергетические уровни, наиболее близко расположенные к дну ямы. так как на дне возмущение наибольшее, а с удалением от дна ямы оно уменьшается п менее влияет на энергию.

Оценивая рафики вероятностей обнаружения частицы в той или иной гонке пространства, для ямы без возмущения и для ямы с вош>ш.сиием. можно едешь вывод, что чем больше энергия частицы, тем больше верояпюегь обнаружения ее ча пределами потенциальной ямы.

6. Список использованной литературы

1. Демиховский В.Я.. Квантовые ямы, нити, точки. Что это такое? Нижегородский государственный университет им. Н.И. Лобачевского, Соросовский образовательный журнал. N 5, 1997 г.

2. Пономарев Л.И. Под знаком кванта, М.: Наука, 1989.

3. Блохинцев Д.И.. Основы квантовой механики, М: Наука. 1976.

4. Филиппов Д,А,. Основы квантовой механики. Великий Новгород: Новгородский государственный университет им. Ярослава Мудрого, 2006

5. Иродов И.Е.. Задачи по квантовой физике. М: Высшая школа, 1991

Date: 2015-05-18; view: 539; Нарушение авторских прав