Упругое рассеяние фотонов на свободных электронах (эффект Комптона)

Эффект Комптона - рассеяние электромагнитной волны на свободном электроне, сопровождающееся уменьшением ее частоты (увеличением длины волны). Эффект Комптона - результат упругого столкновения фотона со свободным электроном. В процессе этого столкновения фотон передает электрону часть своих импульса и энергии в соответствии с законами их сохранения. В результате энергия фотона уменьшается, а длина волны соответственно увеличивается. Электрон, который приобрел кинетическую энергию в результате эффекта Комптона, называют электроном отдачи. Направления движения исходного и рассеянного фотонов и электрона отдачи определяет закон сохранения импульса (рис.3):

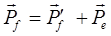, (1.14)

где 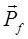- импульс исходного фотона, 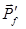- импульс рассеянного фотона, 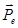- импульс электрона отдачи (рис.3).

Изменение длины волны фотона описывается формулой:

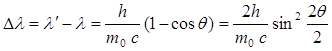, (1.15)

где l и λ΄ - длина волны электромагнитного излучения до и после рассеяния соответственно; m - масса покоя электрона; q - угол рассеяния.

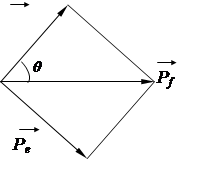Рис.3

Кинетическая энергия электрона отдачи в соответствии с законом сохранения энергии равно разности энергий фотона до и после рассеяния:

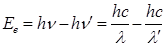, (1.16)

где n и n‘ - частота фотона до и после рассеяния.

Пример 3. Фотон с энергией 100 кэВ рассеялся на свободном электроне на угол q = 60⁰. Найти кинетическую энергию электрона отдачи и направление его движения.

Используя закон сохранения импульса:

,

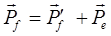необходимо построить схему рассеяния фотона на электроне, отражающую условие задачи (Рис.4):

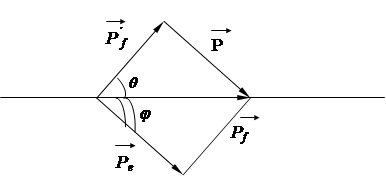Рис.4

На схеме показаны угол рассеяния q и угол j между направлением распространения фотона до рассеяния и направлением движения электрона отдачи, который необходимо найти.

Кинетическая энергия электрона отдачи равна разности энергий до и после рассеяния:

E_e = E_f - E_f’

Энергия фотона до рассеяния дана E_f = 100 кэВ, а энергию фотона после рассеяния следует найти, используя связь между энергией фотона и длиной волны излучения:

E_f’ = hc/l‘.

Согласно формулы (1.15):

следовательно:

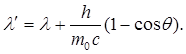
Подставив это выражение в формулу для E_f’, получают:

.

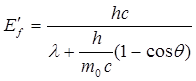Для того, чтобы ввести в эту формулу значение энергии E_f, необходимо разделить числитель и знаменатель на h · c:

Отношение:

,

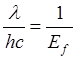следовательно:

.

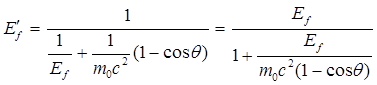Кинетическая энергия электрона отдачи: .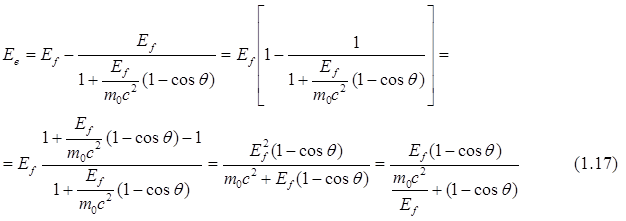

E₀ = m₀ c² – энергия покоя электрона; Е₀ = 9,11·10^-31 кг · 9 · 10¹⁶ м²/с² =

= 8,199 ·10^-14 Дж = 0,512 МэВ = 512 кэВ, так как 1эВ = 1,6·10^-19 Дж.

В формулу (1.17) входит отношение энергий m₀c² / E_f. Поэтому в данном случае энергию фотона Е_f и энергию покоя электрона можно не переводить в джоули, а оставить в кэВ:

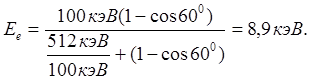
Угол j можно найти следующим образом. Из формулы закона сохранения импульса (1.14) следует, что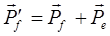

Если возвести в квадрат это уравнение, получают:

.

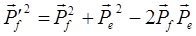Скалярное произведение

.

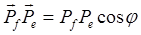Следовательно,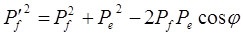

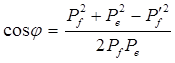(1.18)

Импульс фотона равен (1.2):

.

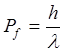Используя связь между энергией фотона и длиной волны, получают:

.

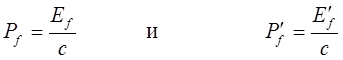Найденное значение энергии электрона отдачи (Е_е = 8,9 кэВ). Много меньше энергии покоя электрона (Е₀ = 512 кэВ), поэтому можно использовать классическое выражение для кинетической энергии:

,

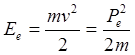из которого получают: Р_е² = 2mЕ_е и .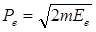

Подставив полученные выражения в формулу (1.18), получают:

.

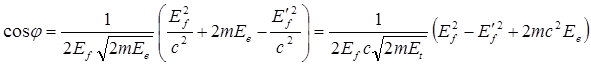Разность квадратов энергий E_f и E_f^' можно представить:

E_f² - E_f^'2 = (E_f – E_f^') (E_f + E_f^') = E_e (2E_f – E_e).

С учетом этого уравнение (1.18) принимает вид:

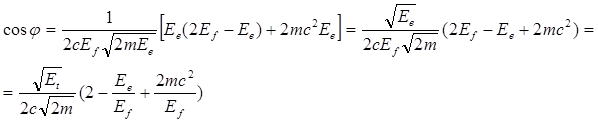
В полученное уравнение следует подставить численные значения и выполнить расчет:

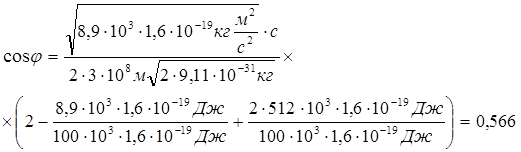
arccos 0,566 = 55°31'

Date: 2015-05-18; view: 2130; Нарушение авторских прав