Стационарное уравнение Шредингера. Если силовое поле, в котором движется частица, стационарно (т.е

Если силовое поле, в котором движется частица, стационарно (т.е. постоянно во времени), то функция U не зависит явно от t. В этом случае решение уравнения Шредингера распадается на два множителя, один из которых зависит только от координат, другой – только от времени:

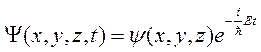(5.10)

Здесь E – полная энергия частицы, которая в случае стационарного внешнего поля остается постоянной. Подставим (5.10) в (5.1):

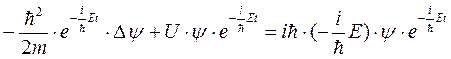(5.11)

Сократив на общий множитель 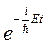, придем к дифференциальному уравнению, определяющему функцию ψ(x, y, z):

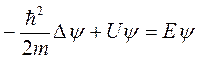(5.12)

Уравнение (5.12) относительно координатной части волновой функции называется стационарным уравнением Шредингера. Далее мы будем иметь дело только с ним.

Это уравнение имеет бесчисленное множество решений, однако при наложении граничных условий, а также упомянутых выше требований (ограниченность, однозначность и непрерывность волновых функций, а также непрерывность частных производных) остается ряд решений, который имеет физический смысл. Эти решения имеют место только при определенных значениях параметра E, которые называются собственными значениями энергии. Совокупность собственных значений Е называется энергетическим спектром. Решения, соответствующие собственным значениям энергии Е, называются собственными функциями задачи.

Простейшей задачей на собственные функции и собственные значения является движение свободной частицы, упомянутой выше. Оно задается уравнением: 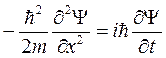(5.13)

Его частным решением является функция 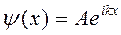, где A=const, ψ(x) является координатной частью волновой функции Ψ(x,t).

Функции ψ(x) соответствуют собственные значения энергии

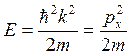(5.14)

где 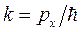. Это выражение верно для нерелятивистской частицы. А поскольку волновое число k может принимать любые положительные значения, то энергетический спектр свободной частицы является непрерывным. Таким образом, свободная частица имеет непрерывный спектр. Для пояснения следует вспомнить спектр излучения электрона в атоме. В этом случае электрон находится в связанном состоянии, и спектр имеет дискретный характер. При отрыве электрона от атома он перестает чувствовать поле ядра, то есть для U → 0, а излучение электрона становится непрерывным, как это предсказывает уравнение Шредингера (5.13).

Date: 2015-05-18; view: 558; Нарушение авторских прав