Лабораторная работа №4. 20. Исследование видимого спектра излучения атома водорода

Цель работы: Целью работы является исследование дифракционного спектра серии Бальмера в видимой области излучения и определение постоянных Ридберга и Планка.

Основные понятия и закономерности

Наиболее заметный вклад в развитие теории строения атомов внес Нильс Бор, однако теория Бора, основанная на известных постулатах, смогла объяснить только строение атома водорода и неприменима для объяснения свойств многоэлектронных атомов. Более универсальная и точная теория строения атомов основана на законах квантовой механики. Основным уравнением квантовой механики является уравнение Шредингера, которое по виду сходно с волновым уравнением, представляет собой дифференциальное уравнение второго порядка в частных производных описывает движение частицы массой m в пространстве с известным распределением потенциальной энергии:

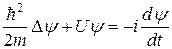, (7.2)

где ,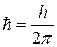

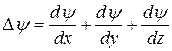- оператор Лапласа,

ψ – волновая функция,

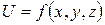- потенциальная функция, описывающая распределение потенциальной энергии,

- мнимая единица,

m – масса микрочастицы.

Из теории дифференциальных уравнений известно, что каждое линейное уравнение в частных производных имеет множество решений. В применении к уравнению (7.2) это означает, что квантовая частица в потенциальном поле может находиться во многих состояниях. Такие состояния определяются начальными и граничными условиями. Среди решений уравнения Шредингера есть стационарные. В каждом стационарном состоянии средние значения всех физических величин не зависят от времени. В частности, для атома водорода потенциальная функция зависит только от координаты r и рассчитывается как потенциальная энергия электрона, находящегося в электрическом поле точечного заряда, сосредоточенного в ядре атома. Волновая функция любого стационарного электрона имеет вид:

, (7.3)

где - зависит только от координаты r.

Состояние стационарно, так как равен единице модуль величины . Поэтому плотность распределения координат частицы от времени не зависит:

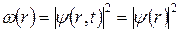, (7.4)

Величина также называется волновой функцией, являясь ее координатной частью. Подставляя (7.3) в (7.2) и учитывая, что:

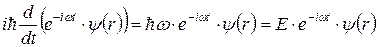, (7.5)

где 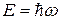- полная энергия электрона.

После сокращения на экспоненту правой и левой частей уравнения (7.5) приходим к стационарному уравнению Шредингера:

, (7.6)

или:

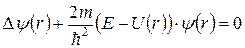. (7.7)

Здесь функция описывает только стационарные состояния электрона с энергией E. Нахождение волновых функций является довольно сложной математической задачей из теории дифференциальных уравнений в частных производных. Ограничимся тем, что приведем результат решения и поясним его физический смысл.

Решения уравнения (7.7) существуют лишь при определенных значениях E, называемых собственными значениями энергии электрона:

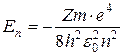(7.8)

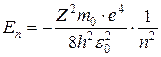(7.9)

где m и e – масса и заряд электрона,

m = 9,1·10^-31 кг,

e = 1,6·10^-19 Кл,

ε₀ = 8,85·10^-12 ф/м – электрическая постоянная,

h = 6,62·10^-34 Дж·с, - постоянная Планка,

Заметим, что аналогичные выражения были получены для полной энергии атома водорода на основе постулатов Бора, которые определяют энергию атома в стационарном состоянии.

Для атома водорода Z = 1. Следовательно, энергия электрона на первой боровской орбите n = 1 равна:

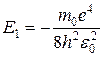. (7.10)

Полная энергия электрона в атоме водорода на орбите с номером n определяется формулой:

. (7.11)

Для водородоподобного иона, в составе которого всего один электрон, а заряд ядра Z_e, энергия электрона равна:

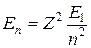. (7.12)

Величина энергии электрона в атоме водорода на первом уровне энергии (орбите) вычисляется по формуле (7.10):

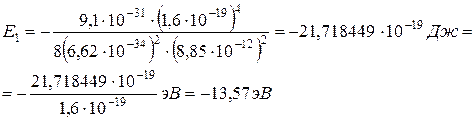
Используя правило частот Бора и найденное значение энергии электрона можно определить частоты, которые излучаются атомом при переходах из одного стационарного состояния в другое:

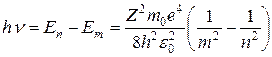(7.13)

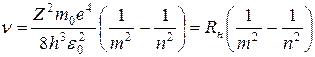, (7.14)

где - постоянная Ридберга (7.15)

Для серии Бальмера m=2, величина n- квантовое число, которое для четырех линий видимого спектра водорода принимает значения 3,4,5 и 6.

Эксперимент по изучению видимой части спектра излучения атомарного водорода проводится с использованием газоразрядной водородной трубки.

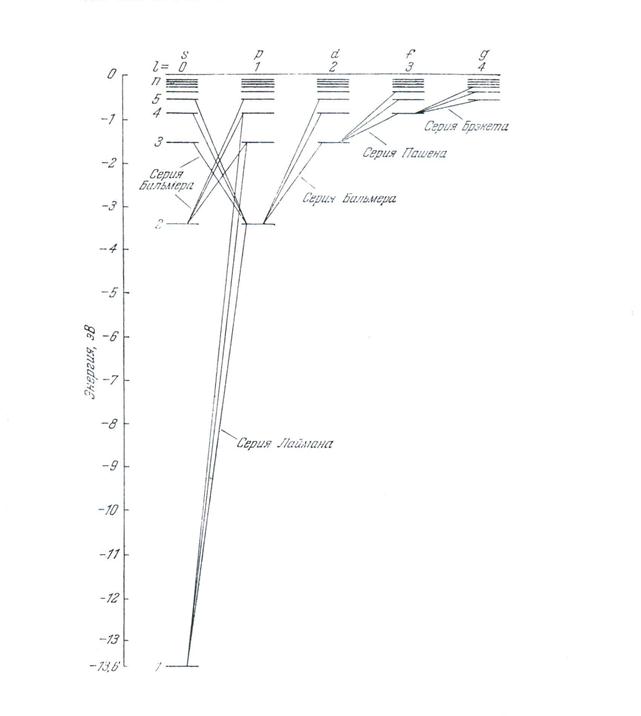
Внутренний объем трубки составляет несколько кубических сантиметров, в этом объеме находится более миллиона атомов. При возникновении электрического разряда большая часть атомов переходит в возбужденное состояние. В возбужденном состоянии атомы находятся короткое время, называемое временем жизни возбужденного атома, а затем релаксируют, излучая избыточную энергию в виде квантов в соответствии со схемой, приведенной на рисунке 1. При этом интенсивность разных спектральных линий оказывается различной и определяется вероятностью того или иного перехода. Наиболее яркими являются линии, образованные переходами между ближайшими уровнями стационарных значений энергии. Такие линии называются головными в каждой серии. В серии Бальмера головной является линия H_α, соответствующая переходу атома из состояния с n=3 в состояние m=2. Кроме того вероятность переходов атома из одного состояния в другое зависит от орбитального квантового числа ℓ, определяющего момент количества движения электрона в атоме. Рассматривая атом водорода как замкнутую систему, необходимо учитывать не только неизменность полной энергии, но и сохранение суммарного момента импульса атома при любых внутренних превращениях, включая переходы из одного энергетического состояния в другое. При этом квант энергии или фотон, который излучается, имеет определенную поляризацию. В квантовой теории единственной направленной величиной является спин или момент количества движения фотона. Состоянию фотона с любой поляризацией соответствуют значения проекции спина S_z= +1 или S_z= -1 на направление его распространения Z.

Таким образом, переходы атома водорода, сопровождающиеся излучением фотона, характеризуются изменением орбитального квантового числа атома на единицу. Это означает, что в квантовых переходах атомов с излучением света число ℓ может меняться только на единицу Δℓ=±1, а состояние атома с f на d, c d на p, с p на S и обратно.

Этот и аналогичные результаты получили название правила отбора. Схема разрешенных кантовых переходов и соответствующие им спектральные линии представлена на рисунке 7.2.

Рисунок 7.2

Целью настоящей лабораторной работы является:

1) измерение длин волн линий в спектре водорода λ₁, λ₂, λ₃, λ₅;

2) вычисление значений постоянной Ридберга;

3) вычисление постоянной Планка с помощью каждого найденного значения длины волны и соответствующего ему значения числа n = 3,4,5,6.

Критерием справедливости сериальной закономерности служит постоянство значения постоянной Ридберга, найденного независимо во всех случаях. Измерение длин волн линий водородного спектра производится при помощи дифракционной решетки и гониометра. Углы φ, под которыми видны максимумы дифракционной решетки, зависит от длины волны измерения и удовлетворяют условию:

, (7.16)

где d – постоянная решетки,

к – порядок спектра испускания,(к=±1, ±2, …)

λ – длина волны,

φ – угол дифракции для данной длины волны.

Из формулы (60) имеем:

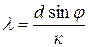. (7.17)

Частоты излучения:

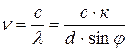, (7.18)

где с = 3·10⁸ м/с – скорость света в вакууме (воздухе).

Из формулы (7.14) определяется постоянная Ридберга:

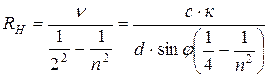, (7.19)

где n = 3,4,5 или 6, а к=±1, ±2, …

Из соотношения (7.15) вычисляется постоянная Планка:

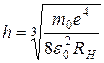. (7.20)

Date: 2015-05-18; view: 984; Нарушение авторских прав