Законы теплового излучения

Закон Кирхгофа утверждает, что отношение спектральной плотности излучения тела к его поглощательной способности в заданном интервале длин волн (или частот) не зависит от природы тела, а является лишь функцией длины волны (или частоты) и температуры, то есть

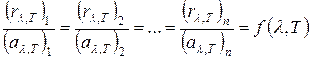. (4.5)

Функция 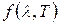есть не что иное, как спектральная плотность излучения абсолютно черного тела, так как закон Кирхгофа справедлив и для абсолютно черного тела:

.

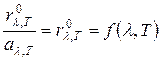Используя закон Кирхгофа, можно по спектральной плотности излучения абсолютно черного тела 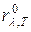определить спектральную плотность излучения любого нечерного тела :

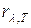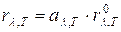. (4.6)

Закон Стефана – Больцмана устанавливает зависимость интегральной плотности излучения абсолютно черного тела R⁰ от температуры: интегральная плотность излучения абсолютно черного тела прямо пропорциональна абсолютной температуре в четвертой степени, то есть

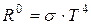, (4.7)

где σ - постоянная Стефана – Больцмана, равная 5,67·10^-8 Вт/м² ·К⁴.

Так как для нечерного тела а_λ,T < 1, то для нечерного тела интегральную плотность излучения R можно определить по закону Стефана – Больцмана, введя коэффициент а_T – суммарный коэффициент поглощения (или степень черноты):

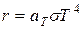. (4.8)

Суммарный коэффициент поглощения а_T нечерного тела определяется по отношению его интегральной плотности излучения R к интегральной плотности излучения абсолютно черного тела R⁰, находящегося при той же температуре:

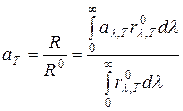. (4.9)

Из закона Стефана – Больцмана следует, что количество теплоты R⁰, передаваемое за единицу времени единицей поверхности абсолютно черного тела, находящегося при температуре T_T, в окружающую среду, имеющую температуру T_ср. (если среду можно принимать за абсолютно черное тело), равно:

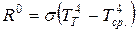. (4.10)

Излучение нечерного тела подчиняется той же зависимости, но его суммарное излучение за единицу времени с единицы поверхности в а_T раз меньше, чем для абсолютно черного тела при той же температуре T_T, то есть:

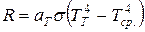. (4.11)

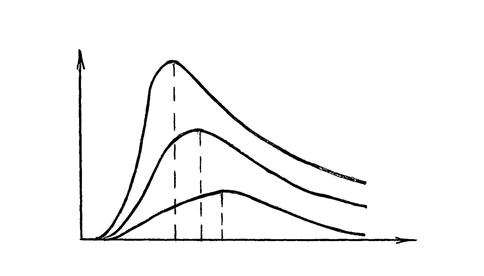Экспериментальные исследования зависимости спектральной плотности излучения абсолютно черного тела от длины волны и температуры (график зависимости 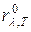от λ приведен на рисунке 4.1) привели к следующим результатам: кривая распределения энергии в спектре излучения абсолютно черного тела имеет четко выраженный максимум,при повышении температуры положение максимума смещается в сторону более коротких волн, а величина максимальной спектральной плотности резко возрастает.

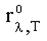
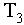
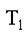
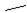
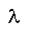
Рисунок 4.1 Спектр теплового излучения абсолютно черного тела при

различных температурах T₃>T₂>T₁

Вину удалось установить, что длина волны λ_max, соответствующая максимуму спектральной плотности излучения, обратно пропорциональна абсолютной температуре тела T:

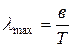, (4.12)

где в – постоянная, равная 2,98·10^-3 м·К.

Соотношение (25) есть первый закон Вина (закон смещения Вина).

Максимальная спектральная плотность излучения определяется вторым законом Вина:

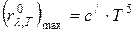, (4.13)

где с^/ - постоянная, равная 1,29·10^-5 Вт·м^-3 ·К^-5.

Основываясь на гипнозе о квантовой природе излучения (атомы излучают энергию отдельными порциями – квантами, имеющими энергию hν, где h – постоянная Планка, равная 6,62·10^-34 Дж·с, а ν – частота излучения) и используя результаты расчета спектральной плотности излучения методами классической физики, Планк получает формулу для спектральной плотности излучения абсолютно черного тела:

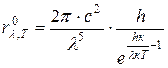. (4.14)

Получившую название формулы Планка, где

h – постоянная Планка;

λ – длина волны излучения;

к – постоянная Больцмана;

T – абсолютная температура тела.

График зависимости спектральной плотности излучения абсолютно черного тела, соответствующей формуле Планка, совпадает с результатами экспериментальных исследований, то есть Планку удалось установить теоретическую зависимость спектральной плотности излучения от длины волны и температуры абсолютно черного тела.

Из формулы Планка (27) можно получить основные законы теплового излучения абсолютно черного тела: Закон Стефана – Больцмана (если проинтегрировать формулу Планка по длине волны), первый и второй закон Вина (если 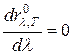, найти длину волны, соответствующую максимуму 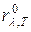, и рассчитать величину максимальной спектральной плотности). Эти вопросы подробно рассмотрены в литературе, например, [1], [2].

В области длин волн, для которых 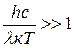, формула Планка примет вид:

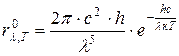, (4.15)

Так как в этом случае единицей в знаменателе формулы Планка (27) можно пренебречь. Соотношение (28) соответствует теоретическому закону Вина, который выполняется в области длин волн, намного меньших длины волны, на которую приходится максимум спектральной плотности излучения.

В области длин волн, для которых 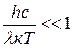, выполняется закон Релея – Джинса, так как в этом случае

и формула примет вид:

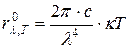. (4.16)

Закон Релея –Джинса выполняется в области длин волн, значительно больших длины волны, на которую приходится максимум излучения.

Date: 2015-05-18; view: 865; Нарушение авторских прав