
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общие сведения. По дисциплине: электростатика
|
|
Кафедра физики
Лабораторная работа №4
По дисциплине: электростатика.
(наименование учебной дисциплины согласно учебному плану)
Тема: Измерение параметров электромагнитного контура
Выполнил: студент гр. ИЗ-07-1_________Стриженок А.В.
(подпись) (Ф.И.О.)
Дата: 6.10.2008г
Проверил: профессор Мустафаев А.С.
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
Цель работы: Экспериментальное определение индуктивности и добротности электромагнитного контура
Общие сведения
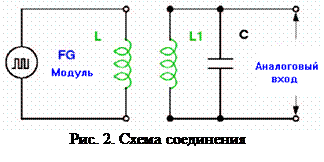 Электрический колебательный контур состоит из ёмкости С, индуктивности L 1 и активного сопротивления R проводов (рис.2). При помощи функционального генератора (FG) напряжение прямоугольных импульсов низкой частоты (f о ≈ 500 Гц) подается на катушку возбуждения L. Резкое изменение магнитного поля вызывает появление напряжения в катушке L 1 и создает за счёт активного сопротивления затухающие свободные колебания в колебательном L 1 C– контуре, частота ƒ (период Т) и амплитуда напряжений которых измеряется с помощью осциллографа (Аналоговый вход CH1). Для контура L 1 C имеются катушки различных длин l, диаметров 2 r и числа витков N (соответствующие значения для номера каждой катушки представлены в таблице 2), емкость считается известной и установлена в разъёмник. Внешний вид всей установки представлен на рисунке 1.
Электрический колебательный контур состоит из ёмкости С, индуктивности L 1 и активного сопротивления R проводов (рис.2). При помощи функционального генератора (FG) напряжение прямоугольных импульсов низкой частоты (f о ≈ 500 Гц) подается на катушку возбуждения L. Резкое изменение магнитного поля вызывает появление напряжения в катушке L 1 и создает за счёт активного сопротивления затухающие свободные колебания в колебательном L 1 C– контуре, частота ƒ (период Т) и амплитуда напряжений которых измеряется с помощью осциллографа (Аналоговый вход CH1). Для контура L 1 C имеются катушки различных длин l, диаметров 2 r и числа витков N (соответствующие значения для номера каждой катушки представлены в таблице 2), емкость считается известной и установлена в разъёмник. Внешний вид всей установки представлен на рисунке 1.
Таким образом, благодаря импульсному характеру наведенного внешнего магнитного поля с катушки L на катушку L 1, в последней возникает индукционный ток, впоследствии чего конденсатор С начинает заряжаться, а потом разряжаться. Такие периодические изменения зарядов, напряжений и токов в контуре носят название электромагнитных колебаний. При этом происходит непрерывный переход энергии электрического поля в конденсаторе в энергию магнитного поля в катушке и обратно. В некоторый момент времени полная энергия колебаний:
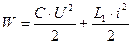 ,
,
где U и i – мгновенные значения разности потенциалов и тока. В те моменты времени, когда конденсатор полностью разряжен (U = 0), ток достигает максимального значения Im , и полная энергия контура равна энергии магнитного поля:
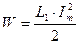
Полная энергия колебаний постепенно уменьшается, так как электрическая энергия благодаря сопротивлению проводов R непрерывно превращается в тепловую и рассеивается в окружающее пространство.
Составим дифференциальное уравнение колебаний в контуре. Пусть q – мгновенное значение заряда на обкладках конденсатора и U – разность потенциалов между обкладками в тот же момент времени. Тогда полное напряжение в цепи 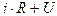 равно сумме действующих ЭДС. Так как в цепи действует только ЭДС самоиндукции:
равно сумме действующих ЭДС. Так как в цепи действует только ЭДС самоиндукции:
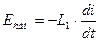 ,
,
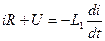 .
.
Подставив в это равенство значения 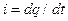 ,
, 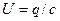 получим:
получим:
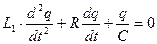 , (1)
, (1)
Разделим обе части уравнения (1) на L 1 и введём обозначения:
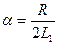 , (2)
, (2)
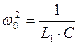 (3)
(3)
где величина a называется коэффициентом затухания; w 0 – собственная частота колебаний контура. Тогда дифференциальное уравнение колебаний примет вид:
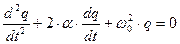 (4)
(4)
 Уравнение (4) – линейное дифференциальное уравнение второго порядка с обыкновенными производными и постоянными коэффициентами. Решения этого уравнения имеют различный вид в зависимости от соотношения между коэффициентами. Положим, что w 0 > a , тогда:
Уравнение (4) – линейное дифференциальное уравнение второго порядка с обыкновенными производными и постоянными коэффициентами. Решения этого уравнения имеют различный вид в зависимости от соотношения между коэффициентами. Положим, что w 0 > a , тогда:
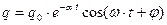 (5)
(5)
где q 0 – максимальное значение заряда на обкладках конденсатора; j – начальная фаза колебаний; w – частота затухающих электрических колебаний:
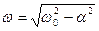 . (6)
. (6)
При R = 0 и a = 0
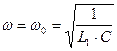 ,
,
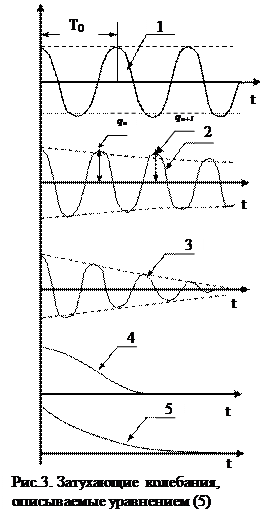
а период этих колебаний (рис.3, кривая 1) составляет:
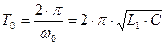 . (7)
. (7)
В случае затухающих колебаний R ¹ 0 (рис.3, кривая 2) и период:
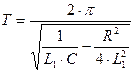 . (7 ’)
. (7 ’)
Решение (5) является аналитическим выражением затухающих колебаний. Большему значению коэффициента a соответствует кривая 3 (рис.3). Хотя затухающие колебания не являются периодическим процессом в строгом смысле этого слова, они обладают определённой повторяемостью в том смысле, что максимальные и минимальные значения заряда, а также тока и напряжения достигаются через одинаковый промежуток времени. Этот промежуток времени и называется периодом Т затухающих колебаний.
Для выяснения физического смысла коэффициента a рассмотрим тепловые потери WR на сопротивлении R за полупериод Т /2:
 ,
,
где < Р > – среднее за период значение тепловой мощности, выделившейся на сопротивлении R. Для синусоидального тока:
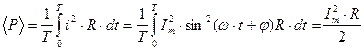 .
.
Полный запас энергии колебательного контура:
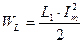 .
.
Отношение энергии, израсходованной в контуре за полупериод на нагревание W R (тепловые потери), к энергии колебаний W L:
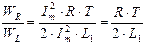 .
.
Используя обозначения (2),получим:
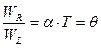 ,
,
где q называется логарифмическим декрементом, который вместе с коэффициентом затухания характеризует потери энергии в контуре.
Как следует из (6), при a > w 0 частота w оказывается мнимой, т.е. колебаний в контуре не будет. Разряд конденсатора будет апериодическим (рис.3 кривая 4 и 5). Логарифмический декремент может быть определён и другим путём. Пусть q n и q n+1 – амплитуды заряда конденсатора в момент времени t n и t n+1, причём t n+1 = t + T. Тогда 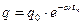 ;
; 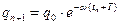 и, следовательно,
и, следовательно,
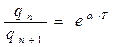 .
.
Как видно из полученного соотношения, отношения последующих амплитудных значений заряда не зависит от номера максимумов и является постоянной величиной для данного контура.
Прологарифмируем соотношение:
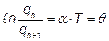 . (8)
. (8)
Таким образом, логарифмический декремент контура можно определить, как натуральный логарифм отношения последующих амплитуд заряда конденсатора. В радиотехнической практике чаще пользуются величиной, обратно пропорциональной логарифмическому декременту q и называемой добротностью Q:
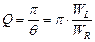 или
или 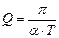 . (9)
. (9)
Добротность контура может быть представлена и так:
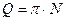
где N – полное число колебаний, за которое амплитуда колебаний уменьшается в е раз. Следовательно, чем выше добротность, тем медленнее рассеивается запас энергии контура.
Если ток силой 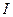 проходит через катушку L 1 (соленоид) длиной
проходит через катушку L 1 (соленоид) длиной 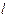 , поперечным сечением
, поперечным сечением 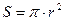 и количеством витков
и количеством витков 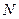 , в катушке возникает магнитное поле. При l >> r магнитное поле однородно, а его напряженность
, в катушке возникает магнитное поле. При l >> r магнитное поле однородно, а его напряженность 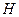 рассчитывается по формуле:
рассчитывается по формуле:
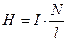 (10)
(10)
Магнитный поток через катушку равен:
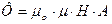 (11)
(11)
где μο –магнитная постоянная, μ – магнитная проницаемость среды.
При изменении магнитного потока возникает напряжение на концах катушки,
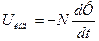
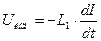 (12)
(12)
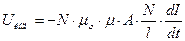
где
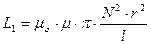 (13)
(13)
является индуктивностью катушки (коэффициентом самоиндукции).
Выражение (13) справедливо только в случае однородного магнитного поля при l >> r.
На практике значение индуктивности катушек при l > r можно рассчитать по формуле:
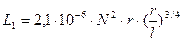 , при
, при 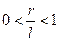 (14)
(14)
В ходе выполнения эксперимента можно рассчитать индуктивность катушек с различными характеристиками, исходя из собственной частоты колебательного контура:
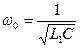 (15)
(15)
Следовательно, индуктивность можно рассчитать по формуле:
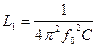 (16)
(16)
Таблица 1. Характеристики катушек
| № катушки | 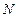
| 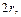 мм мм
| 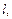 мм мм
| № по каталогу |
| 11006.01 | ||||
| 11006.02 | ||||
| 11006.03 | ||||
| 11006.04 | ||||
| 11006.05 | ||||
| 11006.06 | ||||
| 11006.07 |
| <== предыдущая | | | следующая ==> |
| Пример 5.4.3-1 | | | Теоретическая часть. Разнообразные действия света обусловлены наличием определенной энергии излучения (световой энергии) |
Date: 2015-05-18; view: 551; Нарушение авторских прав