Теоретичні відомості та опис приладів

Дифракцією світла називають зумовлене його хвильовими властивостями явище відхилення від прямолінійності поширення при проходженні світлом середовища з різкими оптичними неоднорідностями.

В залежності від умов спостереження розрізняють – дифракцію Френеля і дифракцію Фраунгофера.

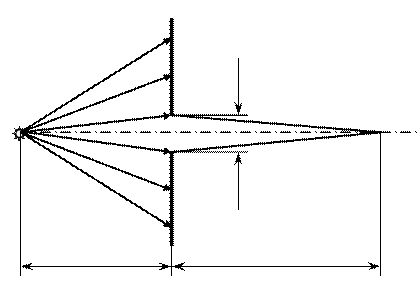
Розглянемо дифракцію світла від джерела S на отворі діафрагми D радіуса R (рис. 1). Якщо точку спостереження О вибрано порівняно близько до отвору, а точніше, якщо

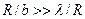, (1)

то йдеться про дифракцію Френеля (дифракцію, що спостерігається при утворенні зображення перепони; сферичний фронт хвилі). Якщо дифракційна картина спостерігається в достатньо далекій точці, тобто якщо

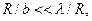(2)

то йдеться про дифракцію Фраунгофера (дифракційне зображення джерела світла). Остання відбувається в паралельних променях (джерело світла і точка спостереження нескінченно віддалені від перепони, на якій відбувається дифракція; плоский фронт хвилі).

D

R

S O

a b

Рис. 1.

Дифракцію Фраунгофера можна дістати, розмістивши між джерелом світла та діафрагмою і між діафрагмою та екраном дві лінзи, щоб точки S та O знаходились у відповідних фокальних площинах.

Математично дифракційні задачі розв′язуються на основі двох принципів:

1. Принцип Гюйгенса: кожна точка фронту хвилі є джерелом елементарних вторинних хвиль (для ізотропних середовищ – сферичних), що поширюються в усіх напрямках, а поверхня, яка охоплює їх через час Δ t, є новим положенням фронту.

2. Принцип Френеля: вторинні хвилі є когерентними і світлове поле в точці спостереження – це результат інтерференції від окремих ділянок фронту вторинних хвиль.

Вивчення явища дифракції світла в загальному полягає у знаходженні розподілу інтенсивності світла на екрані в залежності від геометричних умов (відстаней між джерелом світла, перепоною і екраном). Розподіл інтенсивності світла по екрану залежить також від форми та розмірів отвору. Значний інтерес становить випадок дифракції від щілини.

Щілина – це прямокутний отвір, що має незначну ширину і нескінченну довжину. Практично такою буде щілина, у якої довжина в багато разів більша за її ширину; у переважної більшості щілин це відношення дорівнює 1:1000.

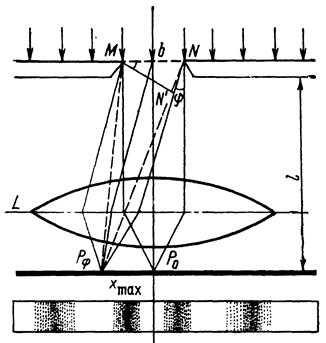Рис. 2.

Якщо на вузьку щілину шириною b падає нормально до поверхні щілини плоска світлова хвиля, відбувається дифракція в обидві сторони (ліворуч і праворуч) від щілини – дифракція Фраунгофера. Як наслідок – зображення щілини на екрані розтягується у смугу з максимумами та мінімумами інтенсивності в перпендикулярному до щілини напрямі.

Наявність максимумів і мінімумів у розподілі інтенсивності світла пояснюється інтерференцією вторинних хвиль, що поширюються у різних напрямах від різних точок щілини (рис. 2). Якщо φ – кут між напрямом падіння променів на щілину і певним розглядуваним напрямом (кут дифракції), то умова максимуму освітленості має такий вигляд

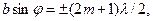(3)

а умова мінімуму

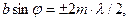(4)

де m – 1, 2, 3, …

Хай на вузьку щілину шириною b нормально до її площини падає монохроматична плоска хвиля. Проведемо вісь координат ОХ упоперек щілини в її площині, вибираючи за початок відліку точку О на краю щілини (див. рис. 3).

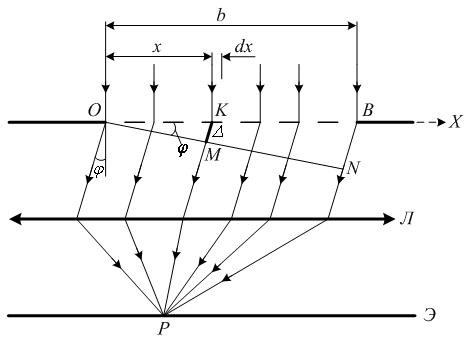
Рис. 3.

Розіб'ємо поверхню щілини (фронту хвилі) на вузькі смужки шириною dx, паралельні довгим краям щілини. Згідно принципу Гюйгенса-Френеля кожна смужка (кожен елемент фронту хвилі або хвильової поверхні) є джерелом вторинної сферичної хвилі, яка викликає коливання з амплітудою прямопропорційною площі смужки, тобто ширині смужки dx. Збиральна лінза, поставлена за щілиною, збирає вторинні паралельні промені в точці Р своєї фокальної площини (рис. 3). Якщо напрям вторинних променів співпадає з напрямом променів, падаючих на щілину, тобто φ = 0, то коливання в точці Р, викликані різними вторинними променями, мають однакові фази

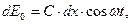
де С – деяка постійна. Інтегруючи цю рівність по всій поверхні щілини і позначаючи амплітуду коливань у фокальній площині лінзи при φ = 0 буквою А₀, отримаємо

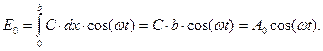
Звідси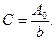

Розглянемо вторинні промені, що відхилилися при дифракції від напряму падаючих променів на кут 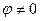. Оскільки фронт хвилі (хвильова поверхня) паралельних променів перпендикулярний променям, то фронт хвилі променів, що відхилилися на кут φ перетинає площину креслення по лінії ON 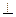BN, а фронт хвилі падаючих променів – по лінії ОВ. До ОВ і після ON до точки Р оптична довжина ходу променів, що проходять через різні точки щілини, однакова, а між ОВ і ON – різна. Зокрема, довжина ходу вторинного променя, що випромінюється точкою К з координатою х, більше довжини ходу променя, що випромінюється точкою О на величину 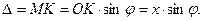Це викликає запізнювання фази коливань на величину 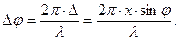Тому в точці Р фокальної площини лінзи складаються коливання 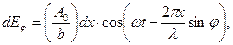викликані вторинними променями від всіх точок щілини, тобто при зміні х від О до b:

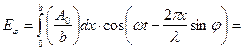
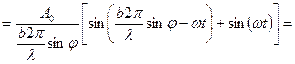
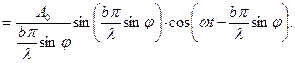(5)

З формули (5) видно, що Е_φ залежить від часу t по гармонійному закону, причому амплітуда коливань А_φ для променів, що відхилилися при дифракції на кут φ, в точці Р фокальної площини лінзи дорівнює

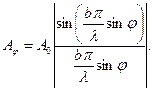
Оскільки інтенсивність світла I прямо пропорційна квадрату амплітуди А², то у фокальній площині лінзи інтенсивність світла I_φ дорівнює

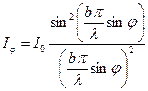, (6)

де I₀ – інтенсивність світла в напрямі падаючої хвилі (φ = 0). Це рівняння свідчить про те, що при освітленні щілини пучком білого світла максимуми та мінімуми відповідних довжин хвиль зміщені один відносно одного. Нульові максимуми для всіх довжин хвиль збігаються, тому в центрі дифракційної картини спостерігається біла смуга, що поступово переходить в кольорову. Далі повинні йти забарвлені в різні кольори максимуми. Але при дифракції від однієї щілини практично не можна побачити чітке розділення для окремих довжин хвиль.

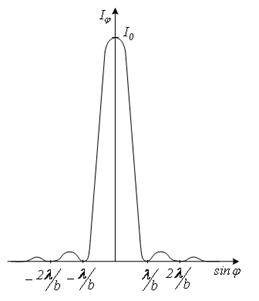
Рис. 4.

На рисунку 4 представлений розподіл інтенсивності світла І_φ при дифракції на щілині шириною b. По осі абсцис відкладені значення .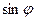

З (6) витікає, що при кутах

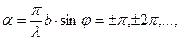(7)

тобто у випадку, якщо

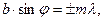(m = 1, 2, 3, …), (8)

інтенсивність І_φ стає рівною нулю (тобто отримана умова мінімумів інтенсивності при дифракції Фраунгофера на одній щілині).

Між мінімумами інтенсивності розташовані максимуми, положення яких може бути визначене рівнянням 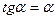, що має корені 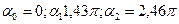і т.д. Значення інтенсивності у максимумах швидко убуває із збільшенням порядку максимумів.

Чисельні значення інтенсивностей головного і наступних максимумів відносяться як

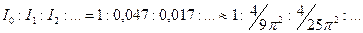(9)

З (9) видно, що основна частина світлового потоку зосереджена в центральній дифракційній смузі, розташованій між мінімумами першого порядку.

З (8) витікає, що кутова ширина головного максимуму за умов m = 1 і 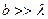дорівнює

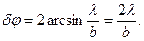(10)

На якість дифракційної картини досить помітно впливає ширина щілини. При збільшенні ширини щілини b кутова ширина максимумів зменшується, при цьому головний (або центральний) максимум стає різкішим і перші мінімуми наближаються до центру дифракційної картини (на рис. 5 b₂ > b₁).

Ширина щілини b не може дорівнювати довжині хвилі λ, бо в цьому випадку 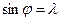, тобто 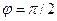. Це означає, що нульовий максимум розпливається по всьому екрану – екран рівномірно освітлений. Якщо b >>λ, то на екрані спостерігається різке зображення щілини, дифракційна картина зникає.

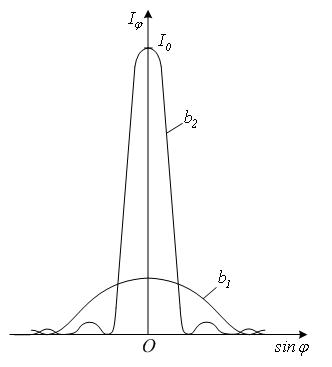
Рис. 5.

У випадку, коли ширина щілини b значно менша за відстань l від щілини до екрана, дифракція Фраунгофера спостерігається і без лінзи L. При цьому промені, що йдуть від країв щілини, практично паралельні. Скориставшись рисунком 2 для випадку дифракції від щілини, дістанемо вираз відстані останнього дифракційного максимуму від центрального:

.

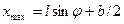Якщо експериментально визначити х_max, l, m, скористатися формулою (3) і відомим значенням λ, то з останньої рівності можна визначити b щілини;

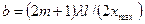. (11)

Рис. 6.

Date: 2015-05-18; view: 621; Нарушение авторских прав