
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные соотношения
|
|
Для студентов специальности РЛ2
Москва 2004
Методические указания рассмотрены и одобрены на заседании кафедры РЛ2
протокол № от
Заведующий кафедрой Козинцев В.И.
д.т.н., профессор
Методические указания содержат перечень основных теоретических вопросов, которые должны быть изучены студентами для выполнения задания; краткие справочные материалы, необходимые для решения задач домашнего задания; примеры решения задач; перечень вариантов задач и таблицу выбора параметров для решения этих задач в зависимости от номера варианта
Теоретический материал
Излучательная и поглощательная способности тел, равновесное тепловое излучение. Закон Кирхгофа. Абсолютно черное тело. Экспериментальные данные по излучению черного тела. Формула Стефана - Больцмана. Закон Релея - Джинса. Закон смещения Вина. Введение Планком представления о кванте излучения. Вывод формулы Планка. Фотометрические величины и единицы измерения. Связь фотометрических величин с вектором Пойнтинга. Спектральные плотности фотометрических величин. Редуцированные фотометрические величины. Фотометрические величины нагретых тел, спектральный коэффициент излучения. Энергетические и световые фотометрические величины. Абсолютная и относительная спектральная световая эффективность. Связь световых и энергетических величин. Индикатриса излучения источника. Эйлеровы и ламбертовы излучатели. Соотношения между фотометрическими величинами. Геометрический и оптический факторы. Инвариант Гершуна. Теорема взаимности.
Основные соотношения
Энергетическая светимость - физическая величина, определяемая отношением потока dФе излучения, исходящего от малого участка поверхности, к площади dA этого участка, Вт/м2:
 . (1)
. (1)
Сила излучения (энергетическая сила света) - физическая величина, определяемая отношением потока dФе излучения, распространяющегося от источника излучения внутри малого телесного угла dω, к этому углу, Вт/ср:
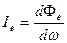 . (2)
. (2)
Облученность (энергетическая освещенность) - физическая величина, определяемая отношением потока излучения dФе, падающего на малый участок поверхности, к площади dА этого участка, Вт/м2:
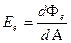 . (3)
. (3)
Энергетическая яркость - физическая величина, определяемая отношением потока излучения d2Фе, переносимого о малой площади dA1 в малом телесном угле dw1, ось которого составляет угол q1 о нормалью к dA1, к геометрическому фактору d2G этого пучка, Вт/(м2ср);
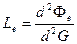 , (4)
, (4)
где
 . (5)
. (5)
Примечание. В том случае, когда геометрический фактор пучка лучей определяется двумя площадками dA1 и dA2, нормали к которым образуют углы θ1 и θ2 с линией, соединяющей центры этих площадок, видимых из центров под углами dw1 и dω2 соответственно, справедливо равенство
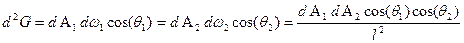 , (6)
, (6)
где l - расстояние между центрами площадок.
Из (4) о учетом (1)-(6) можно получить другие определения энергетической яркости:
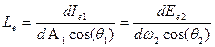 ,
,
где 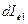 - сила излучения площадки dA1 в направлении под углом θ1 с ее нормалью;
- сила излучения площадки dA1 в направлении под углом θ1 с ее нормалью; 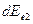 - облученность площадки dA2 и соотношение, связывающее освещенность
- облученность площадки dA2 и соотношение, связывающее освещенность 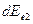 на площадке dA2 от источника с силой излучения dIe, расположенного на расстоянии l от площадки:
на площадке dA2 от источника с силой излучения dIe, расположенного на расстоянии l от площадки:
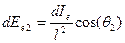 ,
,
где θ2 - угол падения излучения на площадку.
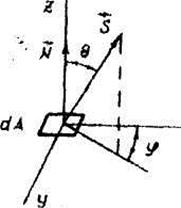
Индикатриса силы излучения — отношение силы излучения Ie в произвольном направлении 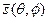 , определяемом угловыми координатами θ и φ, к силе излучения I0 в направлении, принятом за основное (рис.1):
, определяемом угловыми координатами θ и φ, к силе излучения I0 в направлении, принятом за основное (рис.1):
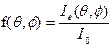 .
.
Если излучателем является площадка dA, а основное направление совпадает о нормалью 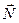 к ней, то
к ней, то
 .
.
 Источники, для которых энергетическая яркость не зависит от направления наблюдения, т.е.
Источники, для которых энергетическая яркость не зависит от направления наблюдения, т.е. 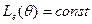 , называются ламбертовыми. Для ламбертовых источников очевидно, что
, называются ламбертовыми. Для ламбертовых источников очевидно, что
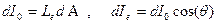 ,
,
и, следовательно, распределение силы излучения симметрично относительно нормали к площадке Для энергетической светимости ламбертова источника получается простое выражение
Рис. 1
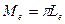 .
.
Спектральные плотности фотометрических величин определяются соотношением
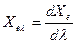 ,
,
где Хе- любая из основных пяти фотометрических величин (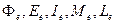 ).
).
Спектральные коэффициенты отражения, поглощения и пропускания ρ(λ),α(λ),τ(λ) определяются выражениями
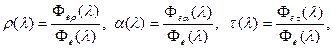
где 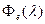 - монохроматический поток излучения, падающий на тело;
- монохроматический поток излучения, падающий на тело;
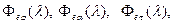 - монохроматические потоки излучения: отраженный, поглощенный телом к прошедший через него соответственно.
- монохроматические потоки излучения: отраженный, поглощенный телом к прошедший через него соответственно.
Интегральные коэффициенты отражения, поглощения и пропускания 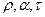 равны
равны
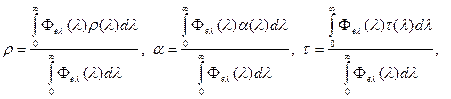
где 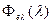 - спектральнаяплотность потока излучения, падающего на тело.
- спектральнаяплотность потока излучения, падающего на тело.
Между 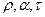 и
и 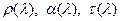 справедливы соотношения
справедливы соотношения
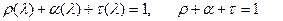 .
.
При падении излучения на тело, для которого выполняются законы отражения и преломления, энергетические яркости отраженного и прошедшего излучения соответственно равны

где Le - энергетическая яркость излучения, падающего на тело; n - относительный показатель преломления сред, находящихся за и перед телом.
Если тело обладает диффузным характером отражения или пропускания, то при создании на нем энергетической освещенности Ee оно становится вторичным ламбертовым излучателем с энергетической яркостью
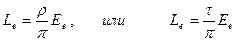 .
.
Редуцированная фотометрическая величина Xr — фотометрическая величина, образованная из соответствующих энергетических величин следующим образом:
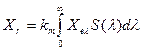 , (7)
, (7)
где S(l) - относительная спектральная чувствительность приемника излучения; Хеλ - спектральная плотность любой энергетической фотометрической величины; Кm - переводной множитель от единиц энергетических величин к единицам, применяемым в системе редуцированных величин.
Примечание. При km =1 редуцированную величину называют относительной редуцированной величиной.
Световая величина Xv - редуцированная фотометрическая величина, определяемая действием излучения на глаз и вычисляемая из (7) при условиях: 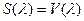 -относительная спектральная световая эффективность (см.таблицу), km - 680 лм/Вт.
-относительная спектральная световая эффективность (см.таблицу), km - 680 лм/Вт.
Система световых величин:
световой поток, лм, 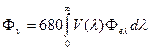 ;
;
яркость, кд/м2, 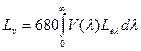 ;
;
сила света, кд, 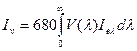 ;
;
освещенность, лк, 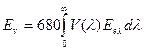 ;
;
светимость, лм/м2, 
Таблица
Относительная спектральная световая эффективность для стандартного фотометрического наблюдателя МКО (дневное зрение)
| λ, нм | V(λ) | λ, нм | V(λ) | λ, нм | V(λ) |
| 0,710 | 0,061 | ||||
| 0,0001 | 0,862 | 0,032 | |||
| 0,0004 | 0,954 | 0,017 | |||
| 0.0022 | 0,995 | 0,0082 | |||
| 0,0040 | 0,995 | 0,0041 | |||
| 0,0116 | 0,952 | 0,0021 | |||
| 0.0230 | 0,870 | 0,00105 | |||
| 0.0380 | 0.757 | 0,00052 | |||
| 0,0600 | 0,631 | 0,00025 | |||
| 0.0910 | 0,503 | 0,00012 | |||
| 0,1390 | 0,381 | 0,00006 | |||
| 0.2080 | 0,265 | 0,00003 | |||
| 0,3230 | 0,175 | 0,000015 | |||
| 0,5030 | 0,107 |
Все предыдущие соотношения для энергетически фотометрических величин применимы к световым величинам. Индексы «е» и «v» в обозначениях фотометрических величин можно опускать, когда соотношения в равной степени могут относиться как к энергетическим, так и световым величинам.
Редуцированные коэффициенты пропускания, отражения и поглощения 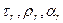 :
:

Спектральная плотность энергетической светимости абсолютно черного тела (а.ч.т.) 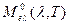 определяется по формуле (закон Планка)
определяется по формуле (закон Планка)

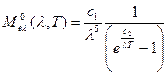 , (8)
, (8)
где Τ - температура а.ч.т., К;
с1 = 3.74ּ10-16 ВтּМ2 = 3.74ּ108 Втּмкм4/м2;
с2 = I.439ּI0-2 мּК = 1,439ּ104 мкмּК.
. Функция 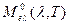 имеет максимум на длине волны, мкм,
имеет максимум на длине волны, мкм,
λm-2896/T
и принимает на этой длине волны значение
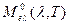 =1.31ּ10-5 T 5 Вт/м3 = 1.31ּ10-11 T 5 Вт/(м2ּмкм).
=1.31ּ10-5 T 5 Вт/м3 = 1.31ּ10-11 T 5 Вт/(м2ּмкм).
Спектральная плотность энергетической светимости реального тела при температуре Т определяется выражением
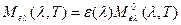 ,
,
где 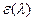 - спектральный коэффициент излучения тела.
- спектральный коэффициент излучения тела.
Date: 2015-05-18; view: 1539; Нарушение авторских прав