
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Опис установки. Для спостереження смуг однакового нахилу використовують світловий пучок з великим кутом розходження
|
|
Для спостереження смуг однакового нахилу використовують світловий пучок з великим кутом розходження, який освітлює прозору плоско-паралельну скляну пластинку. Світло від лазера освітлює об’єктив  (рис. 5) вмонтований у напівпрозорий екран
(рис. 5) вмонтований у напівпрозорий екран  . Завдяки великій оптичній силі об’єктива, пластинка
. Завдяки великій оптичній силі об’єктива, пластинка  освітлюється досить розбіжним світловим пучком. Відбиті від передньої та задньої поверхонь пластинки
освітлюється досить розбіжним світловим пучком. Відбиті від передньої та задньої поверхонь пластинки  хвилі дають на екрані
хвилі дають на екрані 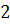 інтерференцію ліній однакового нахилу у вигляді концентричних кіл. Ця картина має локалізуватися у нескінченності, але оскільки
інтерференцію ліній однакового нахилу у вигляді концентричних кіл. Ця картина має локалізуватися у нескінченності, але оскільки 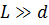 та
та 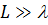 ми її бачимо на скінченній віддалі
ми її бачимо на скінченній віддалі 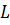 .
.
Спостерігаючи картину ліній однакового нахилу можна визначити максимальний порядок інтерференції при даних 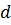 та
та 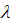 та показник заломлення плоско-паралельної пластинки.
та показник заломлення плоско-паралельної пластинки.
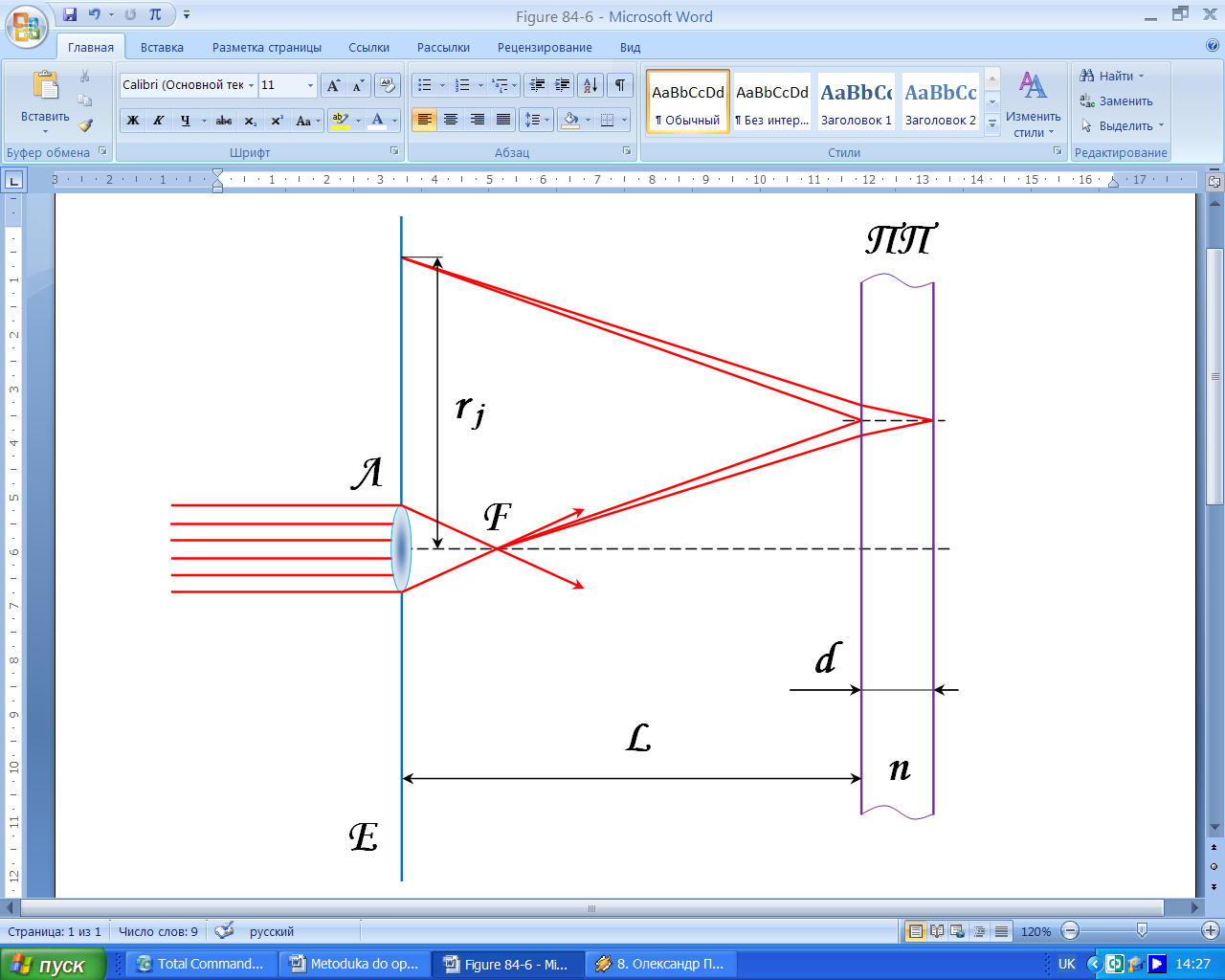
Рисунок 5 – Схема спостереження інтерференційних смуг однакового нахилу.
При візуальному спостереженні інтерференційної картини зручно рахувати та вимірювати темні смуги.
При відбиванні світлової хвилі від границі поділу оптично менш густого з середовищем оптично більш густим фаза коливань світлового вектора 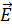 змінюється на
змінюється на 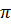 . При відбиванні від границі поділу середовища оптично більш густого з середовищем оптично менш густим такої зміни фази не відбувається. Тому між хвилями виникає додаткова різниця фаз, рівна
. При відбиванні від границі поділу середовища оптично більш густого з середовищем оптично менш густим такої зміни фази не відбувається. Тому між хвилями виникає додаткова різниця фаз, рівна 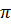 . Її можна врахувати додавши до
. Її можна врахувати додавши до  (або віднявши від неї) половину довжини хвилі у вакуумі.
(або віднявши від неї) половину довжини хвилі у вакуумі.
| (14) |
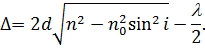
| (15) |
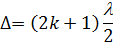
мінімум інтенсивності, а при
| (16) |
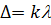
максимуми. Умова максимуму інтенсивності
| (17) |
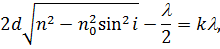
| (18) |
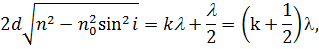
де 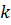 – порядок інтерференційного максимуму. Для повітря
– порядок інтерференційного максимуму. Для повітря 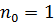 . Можливі для даної пластинки (при заданих
. Можливі для даної пластинки (при заданих 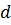 та
та 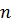 ) значення
) значення 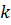 знаходяться у межах:
знаходяться у межах:
| (19) |
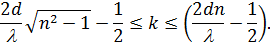
Нижня границя при 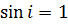 , верхня при
, верхня при 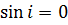 . При дуже малих величинах
. При дуже малих величинах 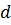 умові (19) задовольняє тільки значення
умові (19) задовольняє тільки значення 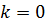 . При великій товщині пластинки можна спостерігати велику кількість максимумів високого порядку Таким чином зі збільшенням товщини пластинки збільшується число інтерференційних максимумів і їх порядок. Будь-яка реальна світлова хвиля являє собою накладання хвиль з частотами, які знаходять в інтервалі
. При великій товщині пластинки можна спостерігати велику кількість максимумів високого порядку Таким чином зі збільшенням товщини пластинки збільшується число інтерференційних максимумів і їх порядок. Будь-яка реальна світлова хвиля являє собою накладання хвиль з частотами, які знаходять в інтервалі 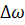 , якому відповідає інтервал довжин хвиль
, якому відповідає інтервал довжин хвиль 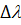 . Навіть у монохроматичного (одноколірного) світла інтервал довжин хвиль малий, але скінченний. Тому інтерференційні максимуми мають скінчену кутову ширину
. Навіть у монохроматичного (одноколірного) світла інтервал довжин хвиль малий, але скінченний. Тому інтерференційні максимуми мають скінчену кутову ширину 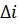 , яку можна знайти продиференціювавши (18) зліва по
, яку можна знайти продиференціювавши (18) зліва по 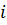 , а справа по
, а справа по 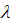 . Отримаємо:
. Отримаємо:
| (20) |
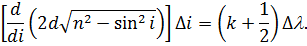
Кутова ширина інтерференційного максимуму:
| (21) |
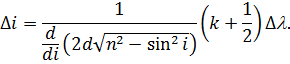
Знайдемо кутову віддаль між сусідніми максимумами (тобто максимумами для яких значення 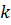 відрізняється на одиницю). Продиференціюємо (18) зліва по
відрізняється на одиницю). Продиференціюємо (18) зліва по 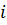 , а справа по
, а справа по 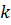 (розглядаючи його як неперервно змінний параметр):
(розглядаючи його як неперервно змінний параметр):
| (22) |
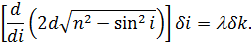
Значення 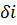 , яке відповідає зміні
, яке відповідає зміні 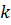 на одиницю (
на одиницю (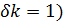 являє собою кутову відстань між сусідніми максимумами:
являє собою кутову відстань між сусідніми максимумами:
| (23) |
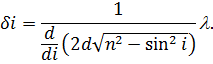
Якщо кутова ширина максимуму 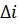 стане рівною по модулю (або перевищить) кутову відстань між сусідніми максимумами
стане рівною по модулю (або перевищить) кутову відстань між сусідніми максимумами 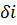 інтерференційна картина повністю розмиється. Тому для спостереження інтерференції при відбиванні світла від прозорих пластин необхідне виконання умови
інтерференційна картина повністю розмиється. Тому для спостереження інтерференції при відбиванні світла від прозорих пластин необхідне виконання умови
| (24) |
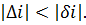
Підставивши значення для 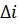 та
та 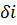 отримаємо:
отримаємо:
| (25) |
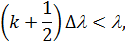
або
| (26) |
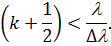
Ми встановили, що порядок максимумів зростає зі збільшенням товщини пластинки. З (26) випливає, що чим більший інтервал довжин хвиль 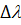 тим меншим повинен бути порядок максимумів, тобто тим менша товщина пластинки, при якій може спостерігатися інтерференція. Згідно (18)
тим меншим повинен бути порядок максимумів, тобто тим менша товщина пластинки, при якій може спостерігатися інтерференція. Згідно (18)
| (27) |
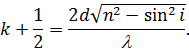
Підставивши у нерівність (26) отримаємо граничну товщину пластинки при якій можна спостерігати інтерференцію:
| (28) |
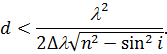
При спостереженні у білому світлі 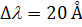 ,
, 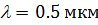 ,
, 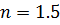 і
і 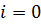 , то
, то 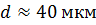 . У монохроматичному світлі
. У монохроматичному світлі 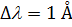 і
і 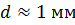 .
.
Для відбитого світла умова мінімуму запишеться:
| (29) |
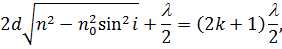
| (30) |
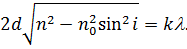
Для повітря 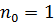 , тоді
, тоді
| (31) |
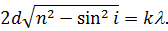
Оскільки кути падіння лазерних променів на екран є невеликі, отримаємо:
| (32) |
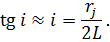
З 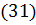 отримаємо, що максимальний порядок інтерференції дорівнює:
отримаємо, що максимальний порядок інтерференції дорівнює:
| (33) |

Користуючись умовою 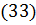 та формулою
та формулою 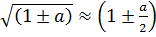 з
з 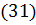 отримаємо:
отримаємо:
| (34) |
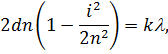
| (35) |
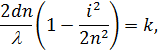
| (36) |
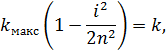
| (37) |
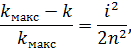
| (38) |
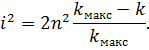
Встановити експериментально порядок 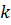 довільного темного кільця неможливо, так як певна невідома їх кількість закрита об’єктивом. Нехай ця кількість буде
довільного темного кільця неможливо, так як певна невідома їх кількість закрита об’єктивом. Нехай ця кількість буде 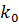 . Перше видиме кільце вважаємо нульовим, а усі наступні
. Перше видиме кільце вважаємо нульовим, а усі наступні 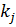 . Тоді вираз
. Тоді вираз 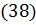 можна записати:
можна записати:
| (39) |
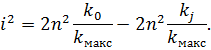
Графічно залежність 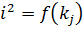 подана на рис. 6. Відстань
подана на рис. 6. Відстань 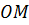 відповідає
відповідає 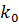 . Цю залежність можна отримати експериментально. За нахилом прямої знаходимо:
. Цю залежність можна отримати експериментально. За нахилом прямої знаходимо:
| (40) |
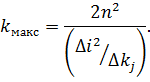
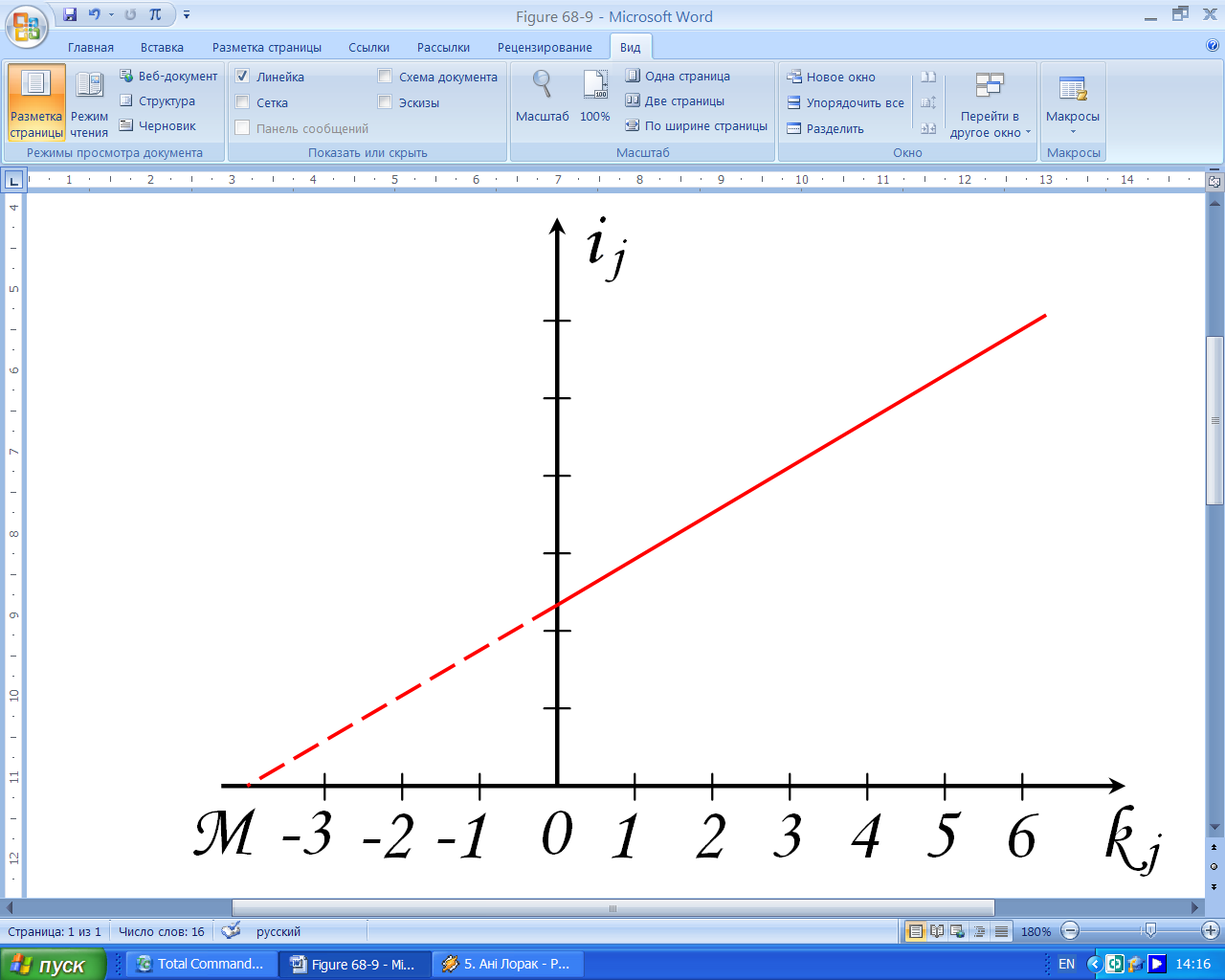
Рисунок 6 – Графік залежності 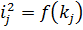 .
.
Якщо невідомий показник заломлення пластинки, то його можна обчислити за допомогою формули:
| (41) |
Date: 2015-05-18; view: 536; Нарушение авторских прав