
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретичні відомості. Розглянемо методи отримання когерентних хвиль в оптиці поділом амплітуди світлової хвилі
|
|
Розглянемо методи отримання когерентних хвиль в оптиці поділом амплітуди світлової хвилі. Ці методи полягають у поділі однієї хвилі на кілька при її відбиванні та заломленні напівпрозорими поверхнями, які частково відбивають і частково пропускають світло. Вони придатні для точкових джерел та для джерел скінченних розмірів і забезпечують значно більшу інтенсивність інтерференційних смуг у порівнянні з методом поділу світлового фронту. Когерентні хвилі можна отримати поділом амплітуди світлової хвилі за допомогою плоско паралельних прозорих пластин, пластин змінної товщини (клин з заломлюючим кутом 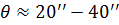 ).
).
Інтерференційні смуги однакової товщини (інтерференція від пластинки змінної товщини). Розглянемо випадок, коли поверхня прозорої пластинки змінної товщини освітлюється протяжним джерелом, розміщеним на досить великій відстані від поверхні пластинки (рис. 1). Розглянемо світлову хвилю, яка поширюється від деякої точки 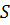 протяжного джерела. Довільна хвиля
протяжного джерела. Довільна хвиля 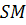 , яка виходить від джерела монохроматичного світла
, яка виходить від джерела монохроматичного світла 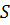 , частково відіб’ється від поверхні
, частково відіб’ється від поверхні 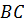 , частково пройде у середину пластинки і відбившись від нижньої поверхні вийде з точки
, частково пройде у середину пластинки і відбившись від нижньої поверхні вийде з точки 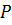 (хвиля
(хвиля 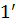 ).У світловому потоці, який йде від джерела
).У світловому потоці, який йде від джерела 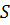 , завжди знайдеться хвиля, яка попаде в точку
, завжди знайдеться хвиля, яка попаде в точку 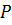 і частково відіб’ється від поверхні пластинки (хвиля
і частково відіб’ється від поверхні пластинки (хвиля 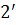 ). При певному взаємному розміщені пластинки і лінзи хвилі
). При певному взаємному розміщені пластинки і лінзи хвилі 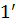 та
та 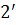 , пройшовши через лінзу, перетнуться в точці
, пройшовши через лінзу, перетнуться в точці 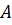 , яка є зображенням точки
, яка є зображенням точки 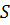 . Оскільки хвилі
. Оскільки хвилі 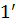 та
та 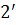 когерентні, то вони будуть інтерферувати і в залежності від різниці ходу між ними в точці
когерентні, то вони будуть інтерферувати і в залежності від різниці ходу між ними в точці 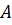 виникне максимум або мінімум. Якщо джерело розміщене досить далеко від поверхні пластинки і кут між поверхнями
виникне максимум або мінімум. Якщо джерело розміщене досить далеко від поверхні пластинки і кут між поверхнями 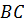 і
і 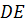 досить малий, то різниця ходу між променями буде приблизно дорівнювати (рис. 1):
досить малий, то різниця ходу між променями буде приблизно дорівнювати (рис. 1):
| (1) |
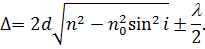
При достатньому віддаленні джерела від поверхні пластинки кути падіння хвиль на пластинку можна вважати рівними. У цьому випадку різниця ходу між інтерферуючими хвилями буде визначатися товщиною пластинки 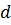 у точці
у точці 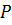 .
.
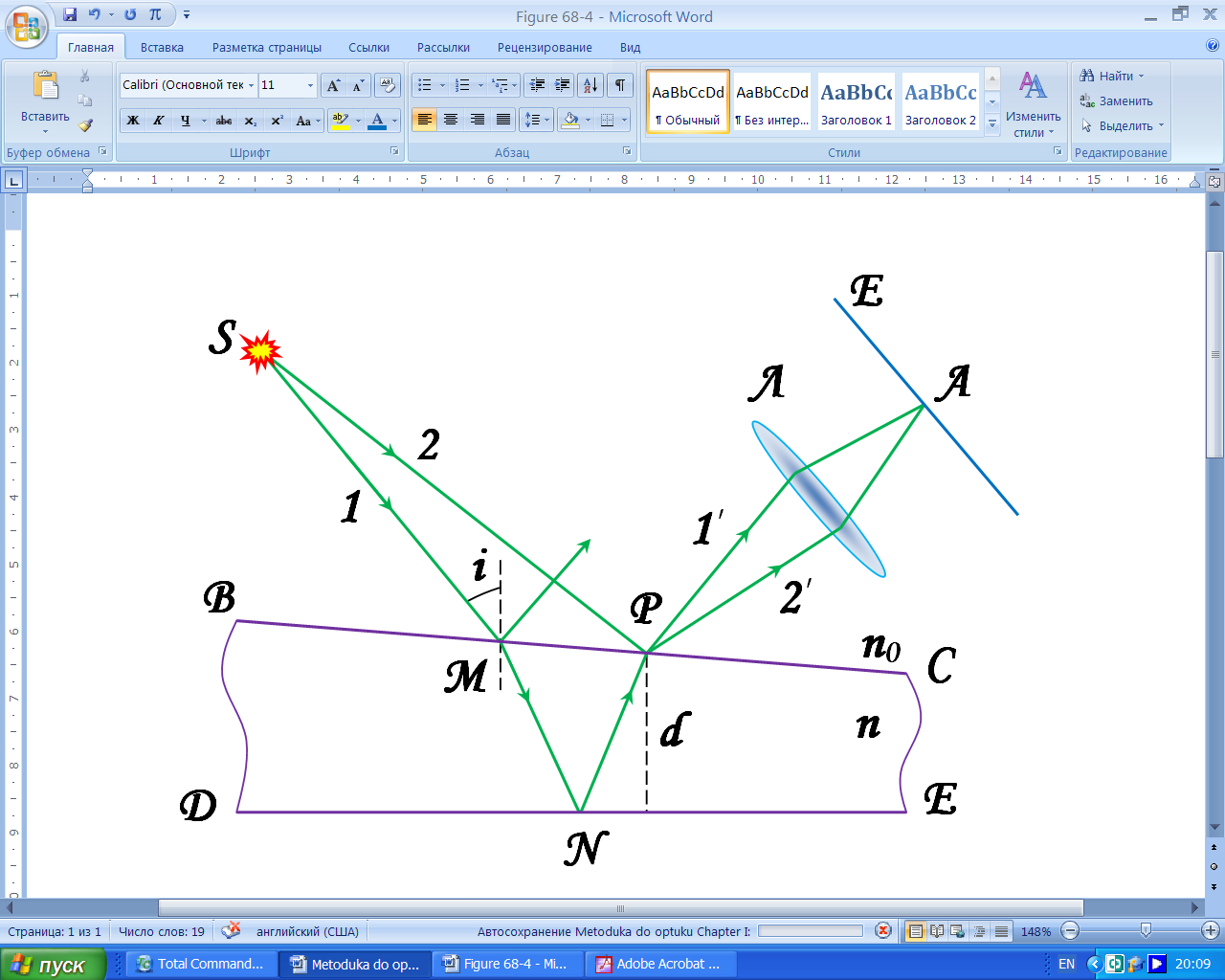
Рисунок 1 – Інтерференція від пластинки змінної товщини.
Звідси випливає, що усім точкам поверхні пластинки однакової товщини відповідає одна й таж інтерференційна картина. Максимуми (або мінімуми) однакової інтенсивності відповідатимуть точкам поверхні, в яких товщина пластинки має одне й теж значення, звідки і походить назва смуги рівної товщини. В залежності від форми пластинки змінюється і форма інтерференційних смуг. Для пластинки у формі клину інтерференційні смуги рівної товщини мають вигляд прямих, паралельних ребру клина. При спостереженні смуг однакової товщини у монохроматичному світлі інтерференційна картина являє собою чергування світлих і темних смуг. При спостереженні у білому світлі плівка забарвлюється у різні кольори. Інтерференцію смуг однакової товщини можна спостерігати на вертикально розміщеній мильній плівці. У такому положенні внаслідок стікання рідини плівка до низу потовщується, у результаті чого вона має змінну товщину.
При використанні точкових джерел (метод поділу фронту) інтерференційна картина не локалізована, вона спостерігається усюди в місцях перекриття інтерферуючих хвиль. На відміну від цього при використанні протяжних джерел (метод поділу амплітуд) інтерференційна картина є локалізована. Місце локалізації інтерференційної картини буде там, де різниця ходу між інтерферуючими променями мінімально буде залежати від кута падіння на пластинку. Ця умова для пластинки змінної товщини задовольняється на її поверхні, а для плоско-паралельної пластинки – в нескінченності.
Кільця Ньютона. Смуги однакової товщини спостерігаються і у випадку, коли з плоскою скляною поверхнею стикається плоско-випукла лінза, радіус кривизни якої 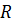 (рис. 3). Вперше це явище описав у 1664 році Роберт Гук, але своєю назвою кільця завдячують Ісаку Ньютону, який детально проаналізував їхню структуру. Між лінзою і пластинкою утворюється повітряний прошарок, який збільшується від точки дотику до країв. Якщо на лінзу нормально падає пучок монохроматичного світла, то світлові хвилі від верхньої і нижньої границі поверхневого шару будуть інтерферувати між собою. Місця рівної товщини поверхневого шару являють собою кільця радіуса
(рис. 3). Вперше це явище описав у 1664 році Роберт Гук, але своєю назвою кільця завдячують Ісаку Ньютону, який детально проаналізував їхню структуру. Між лінзою і пластинкою утворюється повітряний прошарок, який збільшується від точки дотику до країв. Якщо на лінзу нормально падає пучок монохроматичного світла, то світлові хвилі від верхньої і нижньої границі поверхневого шару будуть інтерферувати між собою. Місця рівної товщини поверхневого шару являють собою кільця радіуса 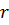 . Нехай паралельний пучок світла направляється на систему лінза-плоско-паралельна пластинка. Деяка хвиля
. Нехай паралельний пучок світла направляється на систему лінза-плоско-паралельна пластинка. Деяка хвиля 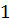 цього пучка після відбивання від нижньої поверхні повітряного прошарку приходить до точки
цього пучка після відбивання від нижньої поверхні повітряного прошарку приходить до точки 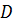 . У цю точку падає також інша хвиля
. У цю точку падає також інша хвиля 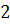 , яка частково відбивається. Дві хвилі
, яка частково відбивається. Дві хвилі 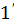 та
та 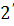 когерентні і при накладанні можуть один одного або посилювати або послаблювати (це залежить від різниці ходу). Оскільки до точки
когерентні і при накладанні можуть один одного або посилювати або послаблювати (це залежить від різниці ходу). Оскільки до точки 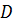 шлях хвилі
шлях хвилі 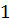 більший, ніж шлях хвилі
більший, ніж шлях хвилі 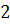 , на віддаль
, на віддаль 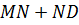 , яка наближено дорівнює
, яка наближено дорівнює 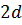 , то відставання хвилі
, то відставання хвилі 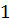 від хвилі
від хвилі 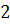 можна прийняти рівним
можна прийняти рівним 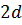 , де
, де 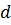 – товщина повітряного прошарку. Крім того, при відбиванні хвиль від оптично більш густішого середовища (у даному випадку скла) втрачається півхвиля
– товщина повітряного прошарку. Крім того, при відбиванні хвиль від оптично більш густішого середовища (у даному випадку скла) втрачається півхвиля  . Додаткова різниця ходу
. Додаткова різниця ходу  обумовлена зміною фази вектора напруженості електричного поля
обумовлена зміною фази вектора напруженості електричного поля 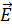 на
на 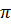 при відбиванні на межі повітря і скла. Отже, хвиля
при відбиванні на межі повітря і скла. Отже, хвиля 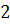 , дійшовши до місця зустрічі у точці
, дійшовши до місця зустрічі у точці 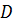 з хвилею
з хвилею 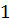 відстає на
відстає на 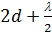 . Якщо ця різниця ходу буде дорівнювати непарному числу півхвилі, то фази коливань обох хвиль на шляху будуть протилежні (хвилі гасять одна одну і пластинка у цьому випадку здається неосвітленою). А та, де різниця ходу дорівнюватиме парному числу півхвилі (фази коливань в обох інтерферуючих хвилях будуть однакові) у відповідному напрямі ми побачимо пластинку освітленою. Оскільки товщина прошарку зростає від точки стикання лінзи з пластинкою, то і різниця ходу буде змінюватися безперервно; вона то дорівнюватиме непарному числу півхвиль то парному числу півхвиль, і тому спостерігається чергування освітлених місць з неосвітленими. Одержимо таку картину: у центрі чорна пляма, оточена рядом концентричних кілець (світлих і темних). У точці дотику лінзи з пластинкою залишається дуже тонкий прошарок товщиною набагато меншою, ніж довжина хвилі. Тому різниця ходу між променями, які виникають у цій точці, визначається лише втратою півхвилі при відбиванні від поверхні плоско-паралельної пластинки. У результаті, різниця ходу дорівнює
. Якщо ця різниця ходу буде дорівнювати непарному числу півхвилі, то фази коливань обох хвиль на шляху будуть протилежні (хвилі гасять одна одну і пластинка у цьому випадку здається неосвітленою). А та, де різниця ходу дорівнюватиме парному числу півхвилі (фази коливань в обох інтерферуючих хвилях будуть однакові) у відповідному напрямі ми побачимо пластинку освітленою. Оскільки товщина прошарку зростає від точки стикання лінзи з пластинкою, то і різниця ходу буде змінюватися безперервно; вона то дорівнюватиме непарному числу півхвиль то парному числу півхвиль, і тому спостерігається чергування освітлених місць з неосвітленими. Одержимо таку картину: у центрі чорна пляма, оточена рядом концентричних кілець (світлих і темних). У точці дотику лінзи з пластинкою залишається дуже тонкий прошарок товщиною набагато меншою, ніж довжина хвилі. Тому різниця ходу між променями, які виникають у цій точці, визначається лише втратою півхвилі при відбиванні від поверхні плоско-паралельної пластинки. У результаті, різниця ходу дорівнює  ; тому у центрі спостерігаємо пляму (рис. 2). Оскільки подібна інтерференційна картина спостерігається за допомогою відбитих хвиль, то її називають інтерференційною картиною у відбитому світлі. Аналогічну картину можна спостерігати і у прохідному світлі.
; тому у центрі спостерігаємо пляму (рис. 2). Оскільки подібна інтерференційна картина спостерігається за допомогою відбитих хвиль, то її називають інтерференційною картиною у відбитому світлі. Аналогічну картину можна спостерігати і у прохідному світлі.
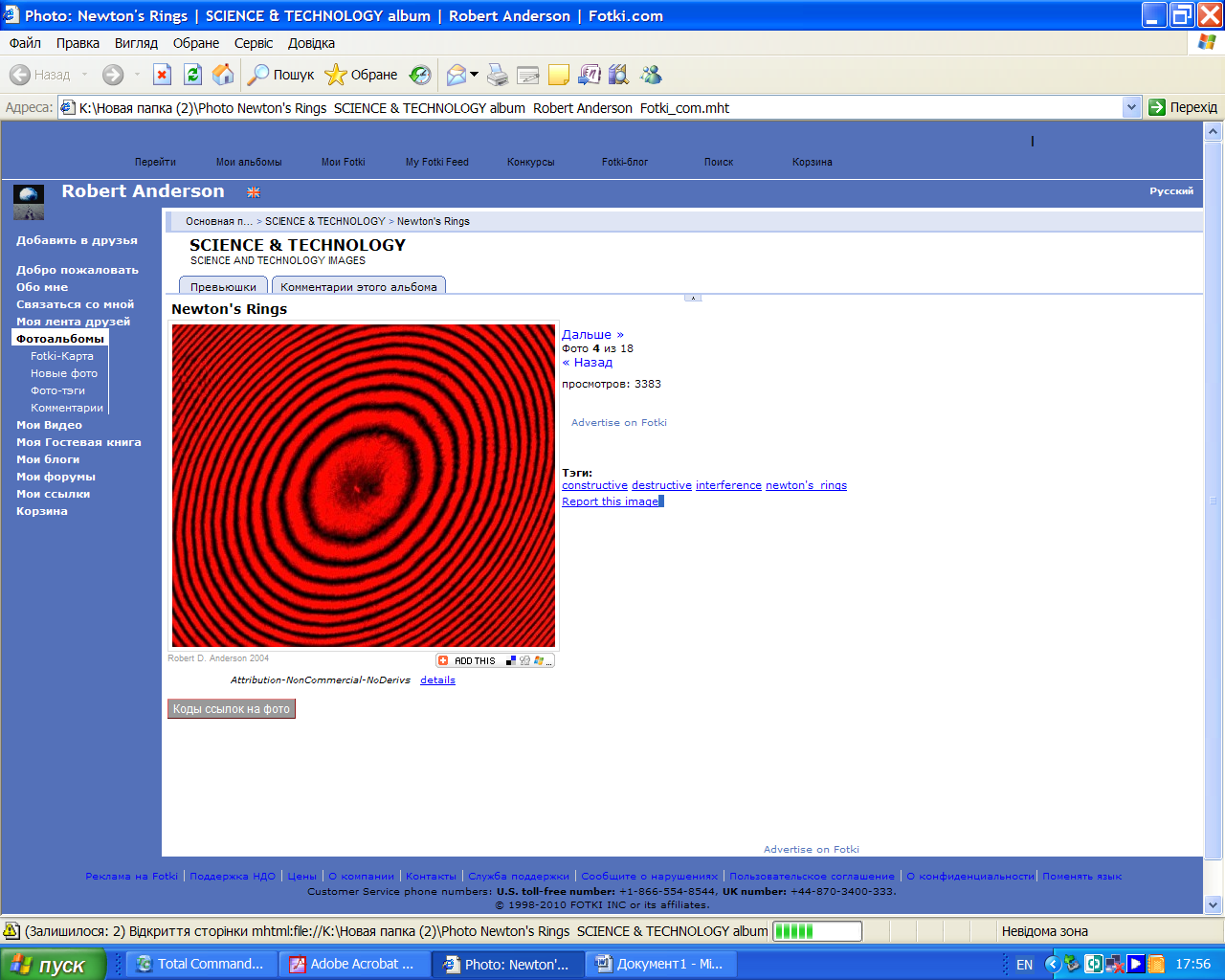
Рисунок 2 – Кільця Ньютона у відбитому світлі при освітленні червоним монохроматичним світлом.
Обчислення різниці ходу інтерферуючих хвиль. Нехай коефіцієнти заломлення пластинки, лінзи і прошарку між ними відповідно будуть 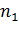 ,
, 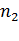 , та
, та 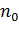 . Різниця ходу хвиль
. Різниця ходу хвиль 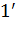 та
та 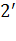 буде:
буде:
| (2) |
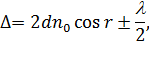
де  – кут заломлення. Знак перед
– кут заломлення. Знак перед 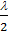 визначається взаємними співвідношеннями між
визначається взаємними співвідношеннями між 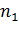 ,
, 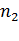 , та
, та 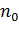 , тобто залежить від того, де (у точці
, тобто залежить від того, де (у точці 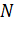 чи у точці
чи у точці 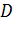 ) відбувається втрата півхвилі.
) відбувається втрата півхвилі.
Якщо лінза і пластинка виготовлені зі скла, а прошарок повітряний (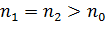 ), то
), то 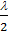 входить у рівняння зі знаком плюс (оскільки втрата півхвилі відбувається на нижній границі повітряного прошарку). При нормальному падінні хвилі
входить у рівняння зі знаком плюс (оскільки втрата півхвилі відбувається на нижній границі повітряного прошарку). При нормальному падінні хвилі 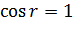 . Вважаючи
. Вважаючи  , отримаємо:
, отримаємо:
| (3) |
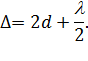
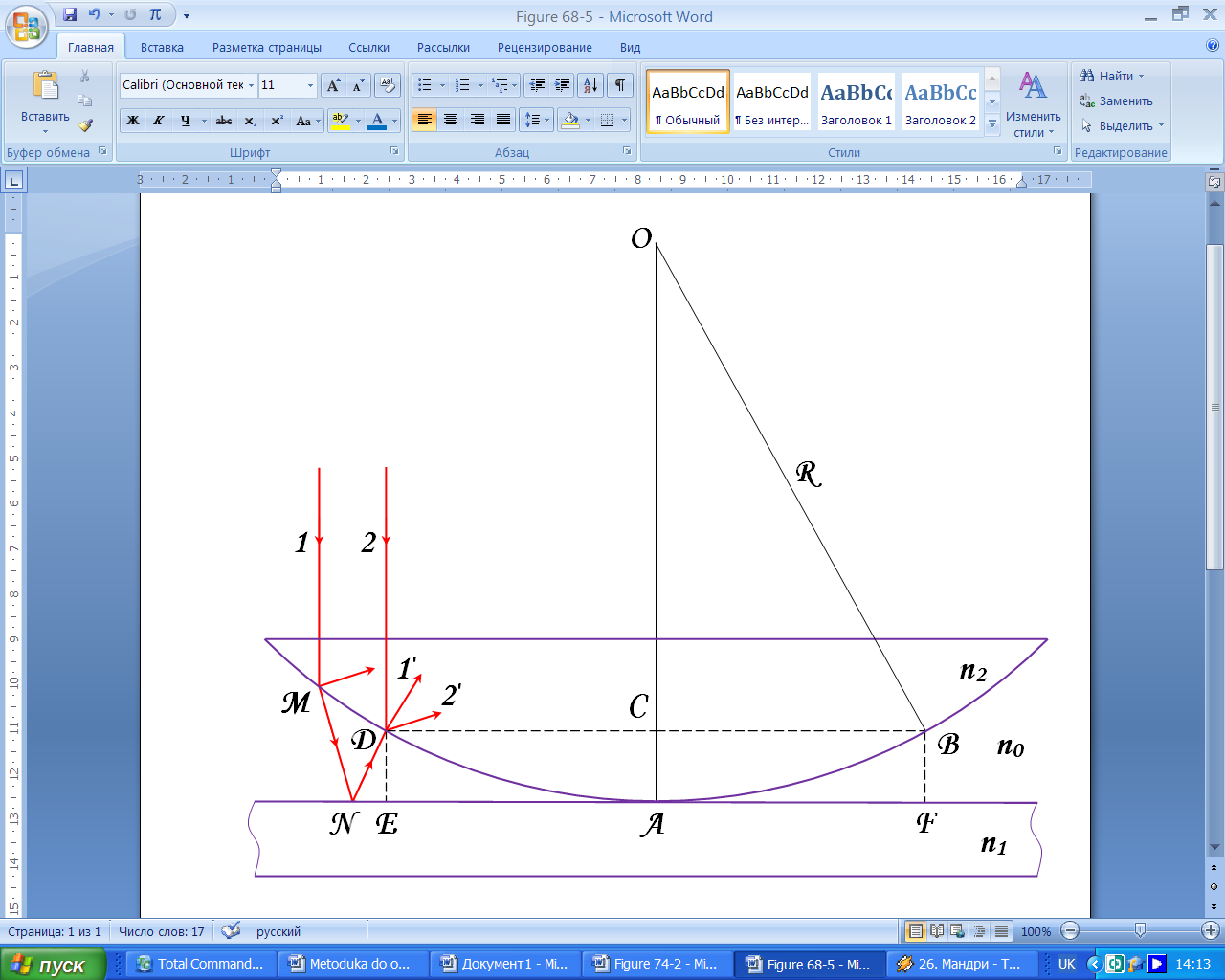
Рисунок 3 – Утворення кілець Ньютона у відбитому світлі.
Розрахунок радіусів для максимумів і мінімумів. Нехай товщина 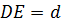 відповідає максимуму
відповідає максимуму 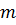 – го порядку, тобто
– го порядку, тобто
| (4) |
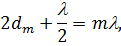
де 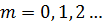 ,
, 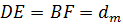 . Тоді радіус для максимуму
. Тоді радіус для максимуму 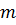 – го порядку буде
– го порядку буде 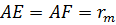 . Виходячи з трикутника
. Виходячи з трикутника 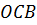 , можна визначити
, можна визначити 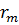 :
:
| (5) |
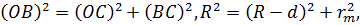
де 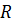 – радіус кривизни лінзи. Вважаючи, що
– радіус кривизни лінзи. Вважаючи, що 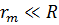 , маємо:
, маємо:
| (6) |
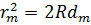
Підставляючи вираз 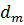 з (4) у (6), отримаємо:
з (4) у (6), отримаємо:
| (7) |
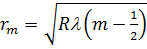
Мінімуми будуть спостерігатися, якщо
| (8) |
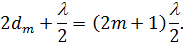
Тоді, радіуси для мінімумів визначаються як
| (9) |
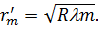
При спостереженні інтерференції у прохідному світлі втрати півхвилі не відбувається і різниця ходу між інтерферуючими хвилями буде дорівнювати:
| (10) |
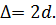
У цьому випадку радіуси для мінімумів та максимумів визначаються відповідно формулами (7) та (9). При освітлені білим світлом внаслідок залежності радіуса кільця від довжини хвилі виникають кольорові кільця. Кільця починаються фіолетовим і закінчуються червоним кольором. Число цих кілець невелике, оскільки при великому 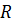 відбувається накладання різних кілець і вони розпливаються. Кільця Ньютона використовуються при виготовленні лінз для визначення правильності кривизни, оскільки вони дуже чутливі до найменших дефектів.
відбувається накладання різних кілець і вони розпливаються. Кільця Ньютона використовуються при виготовленні лінз для визначення правильності кривизни, оскільки вони дуже чутливі до найменших дефектів.
Установка Ньютона дозволяє простим способом визначити довжину світлової хвилі. Для цього достатньо визначити радіус для максимуму даного порядку при відомому радіусі кривизни лінзи.
Запишемо радіус кільця 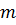 – го та
– го та 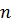 – го порядків відповідно:
– го порядків відповідно:
| (11) |
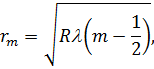
| (12) |
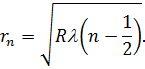
Піднімемо до квадрату обидва рівняння та віднімемо від рівняння 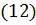 рівняння
рівняння 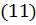 , одержимо:
, одержимо:
| (13) |
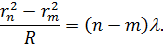
Знаходимо радіус кривизни лінзи і довжину хвилі:
| (14) |
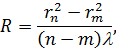
| (15) |
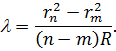
Date: 2015-05-18; view: 1192; Нарушение авторских прав